Лэмбовский сдвиг

Лэмбовский сдвиг  — разница между энергетическими уровнями $^2S_{1/2}$ и $^2P_{1/2}$ в атоме водорода и в водородоподобных ионах, обусловленная взаимодействием атома с нулевыми флуктуациями электромагнитного поля.

Различие между энергиями стационарных состояний $^2S_{1/2}$ и $^2P_{1/2}$ атома объясняются радиационными поправками квантовой электродинамики. Экспериментальное изучение смещения уровней атома водорода и водородоподобных ионов представляет фундаментальный интерес для проверки теоретических основ квантовой электродинамики^[1].

История открытия

Экспериментально установлен У. Ю. Лэмбом (Willis Lamb) и Р. Резерфордом (англ. Robert Retherford) в 1947 году^[2]. В том же году теоретически объяснён Хансом Бете. В 1955 году за свою работу Уиллис Юджин Лэмб был удостоен Нобелевской премии^[3][4]. В 1938 году расчеты, по существу предсказывающие лэмбовский сдвиг, провёл Д. И. Блохинцев, но его работа была отклонена редакцией журнала ЖЭТФ и была опубликована лишь в 1958 году в трудах Д. И. Блохинцева.^[5]

Научно-популярное объяснение

см. также Состояние Фока

Результатом взаимодействия атома с нулевыми колебаниями электромагнитного поля (вакуумные флуктуации поля), являются дополнительные «колебания» электрона, что проявляется в смещении уровня энергии электрона. Это явление называется лэмбовским сдвигом^[6]. Другими словами, сдвиг энергии обусловливается нулевыми флуктуациями, т. е. не равными нулю среднеквадратичными значениями напряженностей электрического (E) и магнитного (B) полей, под действием которых электрический заряд оказывается эффективно как бы размазанным. Это уменьшает действие кулоновского потенциала и повышает уровень энергии s-состояний^[7]. Эффекты, связанные с поляризацией вакуума, т. е. с рождением электрон-позитронных пар, дают относительно малый вклад в Лэмбовский сдвиг^[8].

Суть эффекта

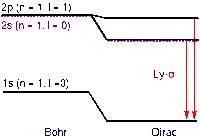Сдвиг уровней водорода состояний $^2S_{1/2}$ и $^2P_{1/2}$. Расчет положения уровней энергии атома без учета (слева) и с учетом (справа) взаимодействия с вакуумными флуктуациями поля.

Сдвиг уровней — это небольшое отклонение тонкой структуры уровней энергии водородоподобных атомов от предсказаний релятивистской квантовой механики, основанных на уравнении Дирака. Согласно точному решению этого уравнения, атомные уровни энергии являются двукратно вырожденными: энергии состояний с одинаковым главным квантовым числом $n = 1, 2, 3,...$ и одинаковым квантовым числом полного момента $j = 1/2, 3/2,...$ должны совпадать независимо от двух возможных значений орбитального квантового числа $l = j \pm 1/2 = n-1$ (исключая $j + 1/2 = n$, когда $l=j-1/2=n-1$) ^{[источник не указан 926 дней]}.

Однако Лэмб и Резерфорд методом радиоспектроскопии обнаружили расщепление уровней 2S_1/2 (n = 2, l = 0, j = 1/2) и 2Р_1/2 (n = 2, l = 1, j = 1/2) в атоме водорода, которые по расчетам Дирака должны были совпадать. Величина сдвига пропорциональна $\alpha^3R$, где $\alpha$ — постоянная тонкой структуры, $R$ — постоянная Ридберга, основной вклад в которую дают два радиационных эффекта ^{[источник не указан 926 дней]}:

1. испускание и поглощение связанным электроном виртуальных фотонов, что приводит к изменению эффективной массы электрона и возникновению у него аномального магнитного момента;
2. возможность виртуального рождения и аннигиляции в вакууме электронно-позитронных пар (т. н. поляризация вакуума), что искажает кулоновский потенциал ядра на расстояниях порядка комптоновской длины волны электрона (~4·10⁻¹¹ см). Найден также вклад эффектов движения и структуры ядра атома водорода (протона).

Значение величины

В работе^[9] измерение лэмбовского сдвига было выполнено при помощи двойного атомного интерферометра. Было получено значение 1057,8514(19)МГц.

Современное теоретическое значение лэмбовского сдвига в водороде L_теор.= (1058,911 ± 0,012) Мгц ^{[источник не указан 926 дней]}. Еще более сильное, чем в атоме водорода, электромагнитное взаимодействие происходит между электронами и ядрами тяжелых атомов. Исследователи из лаборатории GSI (Дармштадт, Германия) пропускали пучок атомов урана (зарядовое число 92) через фольгу, в результате чего атомы теряли все кроме одного из своих электронов, превращаясь в ионы с зарядом +91. Электрическое поле между ядром такого иона и оставшимся электроном достигало величины 10¹⁶ В·см⁻¹. Измеренный лэмбовский сдвиг в ионе составил 468±13 эВ — в согласии с предсказаниями квантовой электродинамики^[10].

Лэмб экспериментально получил значение магнитного момента электрона, которое отличается в 1,001159652200 раз от значения магнетона Бора предсказанного Дираком ^{[источник не указан 926 дней]}. Когда была создана теория перенормировок, лэмбовский сдвиг оказался первым физическим эффектом, на котором подтвердилась её правильность (и, соответственно, правильность квантовой электродинамики, построенной с использованием этой перенормировки) ^{[источник не указан 926 дней]}. Вычисленное новое теоретическое значение оказалось равно 1,001159652415 магнетонам Бора, что поразительно точно совпадает с экспериментом ^{[источник не указан 926 дней]}.

Эксперимент

В 1947 Уиллис Лэмб и Роберт Резерфорд провели эксперимент с использованием микроволнового излучения для стимулирования радиочастотных переходов между квантовыми уровнями атома водорода $2S_{1/2}$ и $2P_{1/2}$. Разница в энергии, найденная Лэмбом и Резерфордом для перехода между $2S_{1/2}$ и $2Sp_{1/2}$ составила ~1060 МГц.

Эта разность — эффект квантовой электродинамики, и может интерпретироваться как влияние виртуальных фотонов, которые испустились и были повторно перепоглощены атомом. В квантовой электродинамике электромагнитное поле квантуется также как и гармонический осциллятор в квантовой механике. Основное состояние поля имеет энергию отличную от нуля $\hbar\omega/2$ (см. Состояния Фока), то есть нулевые колебания поля увеличивают энергию электрона. Радиус орбиты электрона заменяется на величину $~(r+\delta r)$, что изменяет силу Кулоновской связи электрона с ядром, поэтому вырождение уровней $2S_{1/2}$ и $2P_{1/2}$ состояний снимается. Новую энергию уровней можно записать как (используются атомные единицы):

$\langle E_\mathrm{pot} \rangle=-\frac{Ze^2}{4\pi\epsilon_0}\left\langle\frac{1}{r+\delta r}\right\rangle.$

Сам Лэмбовский сдвиг задан

$\Delta E_\mathrm{Lamb}=\alpha^5 m_e c^2 \frac{k(n,0)}{4n^3}\ \mathrm{for}\ \ell=0\,$

и

$\Delta E_\mathrm{Lamb}=\alpha^5 m_e c^2 \frac{1}{4n^3}\left[k(n,\ell)\pm \frac{1}{\pi(j+\frac{1}{2})(\ell+\frac{1}{2})}\right]\ \mathrm{for}\ \ell\ne 0\ \mathrm{and}\ j=\ell\pm\frac{1}{2},$

где $k(n,\ell)$ — малая величина (< 0.05)^[1].

Примечания

1. ↑ ^{1 2} Л. Д. Ландау, Е. М. Лифшиц «Теоретическая физика», в 10 т / В. Б. Берестецкий, Е. М. Лифшиц, Л. П. Питаевский, т. 4, «Квантовая электродинамика», изд. 3, М., «Наука», 1989, ISBN 5-02-014422-3, гл. 12 «Радиационные поправки», п. 123 «Радиационное смещение атомных уровней», c. 605—613;
2. ↑ Лэмб У. Е., Резерфорд Р. К. «Тонкая структура водородного атома», пер. с англ., УФН, 1951, декабрь, т. 45, с. 553—615;
3. ↑ Нобелевская премия по физике 1955 г.
4. ↑ Нобелевская лекция У. Ю. Лэмба
5. ↑ Куземский А. Л. Работы Д. И. Блохинцева и развитие квантовой физики // Физика элементарных частиц и атомного ядра, 2008, т. 39, вып. 1, стр. 30.
6. ↑ А. Б. Мигдал «Качественные методы в квантовой теории», М., «Наука», 1975, гл. 1 «Размерные и модельные оценки», п. 3 «Взаимодействие с излучением», пп «Лэмбовское смещение», с. 68-71;
7. ↑ С Бродский С., Дрелл. С. «Современный статус квантовой электродинамики», УФН, 1972, май, с. 57-99;
8. ↑ [Садовский М.В. «Лекции по квантовой теории поля. Часть 1»;]
9. ↑ Пальчиков В. Г., Соколов Ю. Л., Яковлев В. П. «Время жизни 2p состояния и лэмбовский сдвиг в атоме водорода», «Письма в ЖЭТФ», 1983, т. 38, с. 349;
10. ↑ E. A. Hildum, U. Boesl, D. H. McIntyre, R. G. Beausoleil, and T. W. Hansch Measurement of the 1S-2S frequency in atomic hydrogen (англ.) // Phys. Rev. Lett.. — 1986. — Т. 56. — С. 576—579.

1. ↑ ^{1 2} Л. Д. Ландау, Е. М. Лифшиц «Теоретическая физика», в 10 т / В. Б. Берестецкий, Е. М. Лифшиц, Л. П. Питаевский, т. 4, «Квантовая электродинамика», изд. 3, М., «Наука», 1989, ISBN 5-02-014422-3, гл. 12 «Радиационные поправки», п. 123 «Радиационное смещение атомных уровней», c. 605—613;
2. ↑ Лэмб У. Е., Резерфорд Р. К. «Тонкая структура водородного атома», пер. с англ., УФН, 1951, декабрь, т. 45, с. 553—615;
3. ↑ Нобелевская премия по физике 1955 г.
4. ↑ Нобелевская лекция У. Ю. Лэмба
5. ↑ Куземский А. Л. Работы Д. И. Блохинцева и развитие квантовой физики // Физика элементарных частиц и атомного ядра, 2008, т. 39, вып. 1, стр. 30.
6. ↑ А. Б. Мигдал «Качественные методы в квантовой теории», М., «Наука», 1975, гл. 1 «Размерные и модельные оценки», п. 3 «Взаимодействие с излучением», пп «Лэмбовское смещение», с. 68-71;
7. ↑ С Бродский С., Дрелл. С. «Современный статус квантовой электродинамики», УФН, 1972, май, с. 57-99;
8. ↑ [Садовский М.В. «Лекции по квантовой теории поля. Часть 1»;]
9. ↑ Пальчиков В. Г., Соколов Ю. Л., Яковлев В. П. «Время жизни 2p состояния и лэмбовский сдвиг в атоме водорода», «Письма в ЖЭТФ», 1983, т. 38, с. 349;
10. ↑ E. A. Hildum, U. Boesl, D. H. McIntyre, R. G. Beausoleil, and T. W. Hansch Measurement of the 1S-2S frequency in atomic hydrogen (англ.) // Phys. Rev. Lett.. — 1986. — Т. 56. — С. 576—579.

Литература

• М. О. Скалли, М. С. Зубайри Квантовая оптика / под ред. В. В. Самарцева. — Физматлит, 2003.