Эксцентричная аномалия

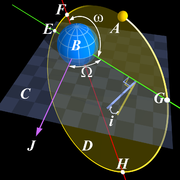
Одной из задач небесной механики является определение орбит небесных тел. Для задания орбиты спутника, планеты, спутника, астероида или Искусственного спутника Земли используют так называемые орбитальные элементы. Они отвечают за задание базовой системы координат (точка отсчёта, оси координат), форму и размер орбиты, её ориентацию в пространстве и момент времени, в который небесное тело находится в определённой точке орбиты. В основном, используются два способа задания (при наличии системы координат):

• при помощи векторов положения и скорости
• при помощи орбитальных элементов^[1]

Кеплеровы элементы орбиты

Основная статья: Кеплеровы элементы орбиты

Элементы орбиты

Традиционно, в качестве элементов орбиты используют шесть кеплеровых элементов орбиты^[2]:

• большая полуось ($a\,\!$)
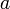• эксцентриситет ($e\,\!$)
• наклонение ($i\,\!$)
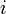• аргумент перицентра ($\omega\,\!$)
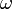• долгота восходящего узла ($\Omega\,\!$)
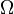• средняя аномалия ($M_o\,\!$)

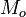Другие элементы орбиты

Аномалии

Аномалии

Аномалия (в небесной механике) — угол используемый для описания движения тела по эллиптической орбите. Истинная аномалия v представляет собой угол между линией, соединяющей тело B с центром эллипса F, и линией соединяющей F с перицентром — точкой на орбите, самой близкой к F.

Основные статьи: Кеплеровы элементы орбиты#Средняя аномалия, Средняя аномалия (кеплеровы элементы орбиты)

Средняя аномалия — для тела, движущегося по невозмущённой орбите — произведение его среднего движения и интервала времени после прохождения перицентра. Таким образом средняя аномалия — угловое расстояние от перицентра гипотетического тела движущегося с постоянной угловой скоростью, равной среднему движению.

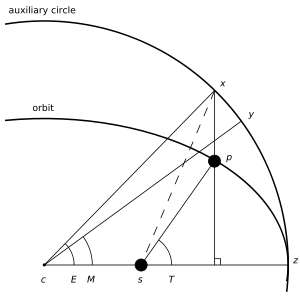
Эксцентрическая аномалия (обозначается E) — параметр используемый для выражения переменной длины радиус-вектора r. Уравнение связывающее эти величины имеет вид:

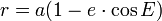$r = a(1-e \cdot \cos E)$, где

a — большая полуось,

e — эксцентриситет эллиптической орбиты.

Истинная аномалия - угол между большой полуосью и лучом из фокуса в положение (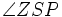$\angle ZSP$). Отсчитывается от перицентра.

Примечания

1. ↑ Дубошин Г. Н. Справочное руководство по небесной механике и астродинамике
2. ↑ Здесь и далее рассматривается задача двух тел