- Фунциональная последовательность
-
Содержание
Функциональная последовательность
Пусть задана последовательность комплекснозначных функций на множестве
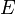 включенном в d-мерное евклидово пространство
включенном в d-мерное евклидово пространство 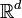 .
.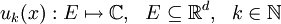
Поточечная сходимость
Числовая последовательность
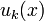 сходится поточечно к числовой последовательности
сходится поточечно к числовой последовательности 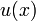 , если
, если 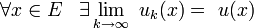 .
.Равномерная сходимость
Существует функция
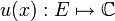 такая, что:
такая, что: 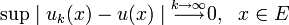
Факт равномерной сходимости последовательности
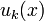 к функции
к функции 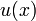 записывается:
записывается: 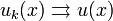
Критерий Коши равномерной сходимости
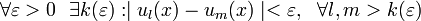
Функциональный ряд
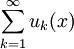
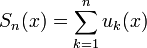 — n-ная частичная сумма.
— n-ная частичная сумма.В этом разделе всё происходит на множестве
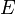
Поточечная сходимость
Последовательность
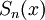 сходится поточечно.
сходится поточечно.Равномерная сходимость
Последовательность
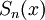 сходится равномерно.
сходится равномерно.Необходимое условие равномерной сходимости
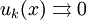
Критерий Коши равномерной сходимости
Критерий Коши для последовательности
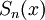 .
.Абсолютная сходимость
Ряд
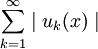 сходится.
сходится.Признаки равномерной сходимости
Признак сравнения
Ряд
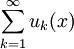 сходится абсолютно и равномерно, если выполнены условия:
сходится абсолютно и равномерно, если выполнены условия:- Ряд
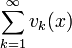 сходится равномерно.
сходится равномерно. 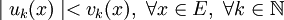
Признак Вейерштрасса
Ряд
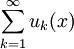 сходится абсолютно и равномерно, если выполнены условия:
сходится абсолютно и равномерно, если выполнены условия:- Числовой ряд
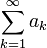 сходится.
сходится. 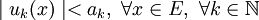
Признак Дирихле
Ряд
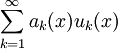 сходится равномерно, если выполнены следующие условия:
сходится равномерно, если выполнены следующие условия:- Последовательность действительнозначных функций
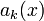 монотонна
монотонна 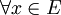 и
и 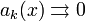
- Частичные суммы
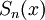 ряда
ряда 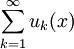 равномерно ограничены.
равномерно ограничены.
Признак Абеля
Ряд
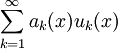 сходится равномерно, если выполнены следующие условия:
сходится равномерно, если выполнены следующие условия:- Последовательность действительнозначных функций
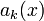 равномерно ограничена и монотонна
равномерно ограничена и монотонна 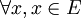 .
. - Ряд
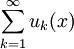 равномерно сходится.
равномерно сходится.
Свойства равномерно сходящихся последовательностей и рядов
Теоремы о непрерывности
Рассматривается комплекснозначные функции на множестве
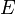
Последовательность непрерывных в точке функций сходится к функции непрерывной в этой точке.
- Последовательность
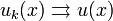
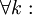 функция
функция 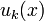 непрерывна в точке
непрерывна в точке 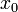
- Тогда
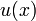 непрерывна в
непрерывна в 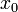 .
.
Ряд непрерывных в точке функций сходится к функции непрерывной в этой точке.
- Ряд
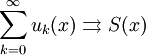
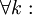 функция
функция 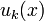 непрерывна в точке
непрерывна в точке 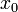
- Тогда
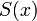 непрерывна в
непрерывна в 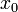 .
.
Теоремы об интегрировании
Рассматриваются действительнозначные функции на отрезке действительной оси.
Теорема о переходе к пределу под знаком интеграла.
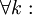 функция
функция 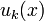 непрерывна на отрезке
непрерывна на отрезке ![\ [a, b]](/pictures/wiki/files/53/5fc1fbc48b5a353c0095a0f55f520e32.png)
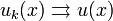 на
на ![\ [a, b]](/pictures/wiki/files/53/5fc1fbc48b5a353c0095a0f55f520e32.png)
- Тогда
![\ \int\limits_{a}^{x} {u_k}(x)dx \rightrightarrows \int\limits_{a}^{x} u(x)dx~,~~\forall x \in [a,b]](/pictures/wiki/files/56/8d6c04ff102595692f112fd72b856341.png)
Теорема о почленном интегрировании.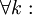 функция
функция 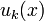 непрерывна на отрезке
непрерывна на отрезке ![\ [a, b]](/pictures/wiki/files/53/5fc1fbc48b5a353c0095a0f55f520e32.png)
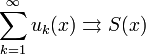 на
на ![\ [a, b]](/pictures/wiki/files/53/5fc1fbc48b5a353c0095a0f55f520e32.png)
- Тогда
![\ \sum_{k=1}^{\infty}\int\limits_{a}^{x} {u_k}(x)dx \rightrightarrows \int\limits_{a}^{x} S(x)dx~,~~\forall x \in [a,b]](/pictures/wiki/files/97/a48f097388befbd9163a81ca05f06643.png)
Теоремы о дифференцировании
Рассматриваются действительнозначные функции на отрезке действительной оси.
Теорема о дифференцировании под пределом.
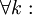 функция
функция 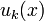 непрерывна дифференцируема на отрезке
непрерывна дифференцируема на отрезке ![\ [a, b]](/pictures/wiki/files/53/5fc1fbc48b5a353c0095a0f55f520e32.png)
![\ \exist c\in [a, b]:~u_k(c)](/pictures/wiki/files/98/b2e1ccf149c70adc16ae213ee56cd1eb.png) сходится
сходится
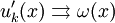 на отрезке
на отрезке ![\ [a, b]](/pictures/wiki/files/53/5fc1fbc48b5a353c0095a0f55f520e32.png)
- Тогда
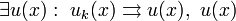 - непрерывно дифференцируема на
- непрерывно дифференцируема на ![\ [a, b]](/pictures/wiki/files/53/5fc1fbc48b5a353c0095a0f55f520e32.png) ,
, 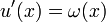 на
на ![\ [a, b]](/pictures/wiki/files/53/5fc1fbc48b5a353c0095a0f55f520e32.png)
Теорема о почленном дифференцировании.
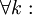 функция
функция 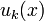 непрерывно дифференцируема на отрезке
непрерывно дифференцируема на отрезке ![\ [a, b]](/pictures/wiki/files/53/5fc1fbc48b5a353c0095a0f55f520e32.png)
![\ \exist c\in [a, b]:~ \sum_{k=1}^{\infty} u_k(c)](/pictures/wiki/files/100/da5c1c11227b0f514f86a2f7c63010b4.png) сходится
сходится
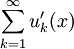 равномерно сходится на отрезке
равномерно сходится на отрезке ![\ [a, b]](/pictures/wiki/files/53/5fc1fbc48b5a353c0095a0f55f520e32.png)
- Тогда
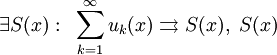 - непрерывно дифференцируема на
- непрерывно дифференцируема на ![\ [a, b]](/pictures/wiki/files/53/5fc1fbc48b5a353c0095a0f55f520e32.png) ,
, 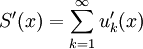 на
на ![\ [a, b]](/pictures/wiki/files/53/5fc1fbc48b5a353c0095a0f55f520e32.png)
Ссылки
- О.В.Бесов Лекции по математическому анализу Ч. 1. — М.: МФТИ, 2004. — 327 с. Глава 16 Функциональные последовательности и ряды
- Ряд
Wikimedia Foundation. 2010.
