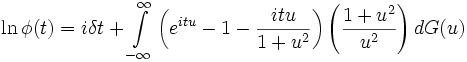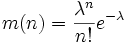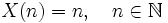Формула Леви — Хинчина для бесконечно делимого распределения

Бесконе́чно дели́мое распределе́ние в теории вероятностей это распределение случайной величины такой, что она может быть представлена в виде произвольного количества независимых, одинаково распределённых слагаемых.

Определение

Случайная величина Y называется бесконечно делимой, если для любого 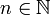$n \in \mathbb{N}$ она может быть представлена в виде

$Y = \sum\limits_{i=1}^n X^{(n)}_i$,

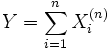где 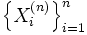$\left\{X_i^{(n)}\right\}_{i=1}^n$ - независимые, одинаково распределённые случайные величины.

Свойства бесконечно делимых распределений

• Характеристическая функция φ_Y(t) бесконечно делимой случайной величины Y имеет вид:

$\phi_Y(t) = \phi^n_{X^{(n)}}(t)$.

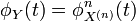Канонические представления бесконечно делимых распределений

Формула Колмогорова

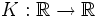Пусть φ(t) - характеристическая функция бесконечно делимого распределения на $\mathbb{R}$. Тогда существует неубывающая функция $K:\mathbb{R} \to \mathbb{R}$, такая что 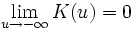$\lim\limits_{u \to -\infty} K(u) = 0$, и

$\ln \phi(t) = i\delta t + \int\limits_{-\infty}^{\infty} \frac{e^{it u} - 1 - i u t}{u^2} \, dK(u)$,

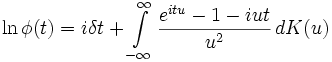где интеграл понимается в смысле Лебега — Стилтьеса.

Формула Леви — Хинчина

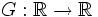Пусть φ(t) - характеристическая функция бесконечно делимого распределения на $\mathbb{R}$. Тогда существует неубывающая функция ограниченной вариации $G:\mathbb{R} \to \mathbb{R}$, такая что

$\ln \phi(t) = i \delta t + \int\limits_{-\infty}^{\infty}\left(e^{itu} - 1 - \frac{itu}{1+u^2}\right)\left(\frac{1+u^2}{u^2}\right)dG(u)$

Примеры

• Следующие распределения бесконечно делимы: распределение Коши, распределение Пуассона, нормальное распределение, гамма распределение.

• Пусть задано вероятностное пространство 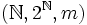$(\mathbb{N},2^{\mathbb{N}},m)$, где

$m(n) = \frac{\lambda^n}{n!} e^{-\lambda}$

для некоторого λ > 0. Тогда случайная величина 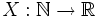$X:\mathbb{N} \to \mathbb{R}$, имеющая вид

$X(n) = n,\quad n \in \mathbb{N}$

не является бесконечно делимой.

См. также

• Устойчивое распределение.