- Проблема трёх заключенных
-
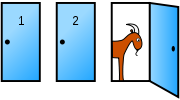 В поисках автомобиля, игрок выбирает дверь 1. Тогда ведущий открывает 3-ю дверь, за которой находится коза, и предлагает игроку изменить свой выбор на дверь 2. Стоит ли ему это делать?
В поисках автомобиля, игрок выбирает дверь 1. Тогда ведущий открывает 3-ю дверь, за которой находится коза, и предлагает игроку изменить свой выбор на дверь 2. Стоит ли ему это делать?Парадо́кс Мо́нти Хо́лла — одна из известных задач теории вероятностей, решение которой, на первый взгляд, противоречит здравому смыслу. Задача формулируется как описание гипотетической игры, основанной на американском телешоу «Let’s Make a Deal», и названа в честь ведущего этой передачи. Наиболее распространенная формулировка этой задачи, опубликованная в 1990 году в журнале Parade Magazine, звучит следующим образом:
Представьте, что вы стали участником игры, в которой вам нужно выбрать одну из трех дверей. За одной из дверей находится автомобиль, за двумя другими дверями — козы. Вы выбираете одну из дверей, например, номер 1, после этого ведущий, который знает, где находится автомобиль, а где — козы, открывает одну из оставшихся дверей, например, номер 3, за которой находится коза. После этого он спрашивает вас, не желаете ли вы изменить свой выбор и выбрать дверь номер 2. Увеличатся ли ваши шансы выиграть автомобиль, если вы примете предложение ведущего и измените свой выбор ?
Хотя данная формулировка задачи является наиболее известной, она несколько проблематична, поскольку оставляет некоторые важные условия задачи неопределенными. Ниже приводится более полная формулировка.
При решении этой задачи обычно рассуждают примерно так: после того, как ведущий открыл дверь, за которой находится коза, автомобиль может быть только за одной из двух оставшихся дверей. Поскольку игрок не может получить никакой дополнительной информации о том, за какой дверью находится автомобиль, то вероятность нахождения автомобиля за каждой из дверей одинакова, и изменение первоначального выбора двери не дает игроку никаких преимуществ. Однако такой ход рассуждений неверен. Если ведущий всегда знает, за какой дверью что находится, всегда открывает ту из оставшихся дверей, за которой находится коза, и всегда предлагает игроку изменить свой выбор, то вероятность того, что автомобиль находится за выбранной игроком дверью, равна 1/3, и, соответственно, вероятность того, что автомобиль находится за оставшейся дверью, равна 2/3. Таким образом, изменение первоначального выбора увеличивает шансы игрока выиграть автомобиль в 2 раза. Этот вывод противоречит интуитивному восприятию ситуации большинством людей, поэтому описанная задача и называется парадоксом Монти Холла.
Содержание
Задача и решение
Более точная формулировка задачи
Наиболее распространённая формулировка задачи, опубликованная в журнале Parade, к сожалению, не вполне точна, поскольку оставляет неопределёнными несколько существенных условий. Более полная и точная формулировка задачи выглядит примерно так:
Представьте, что вы стали участником игры, в которой вы находитесь перед тремя дверями. Ведущий, о котором известно, что он честен, поместил за одной из дверей автомобиль, а за двумя другими дверями — по козе. У вас нет никакой информации о том, что за какой дверью находится. Ведущий говорит вам: «Сначала вы должны выбрать одну из дверей. После этого я открою одну из оставшихся дверей, за которой находится коза. Затем я предложу вам изменить свой первоначальный выбор и выбрать оставшуюся закрытую дверь вместо той, которую вы выбрали вначале. Вы можете последовать моему совету и выбрать другую дверь, либо подтвердить свой первоначальный выбор. После этого я открою дверь, которую вы выбрали, и вы выиграете то, что находится за этой дверью.»
Вы выбираете дверь номер 3. Ведущий открывает дверь номер 1 и показывает, что за ней находится коза. Затем ведущий предлагает вам выбрать дверь номер 2. Увеличатся ли ваши шансы выиграть автомобиль, если вы последуете его совету ?
В данной задаче также неявно предполагается, что открытие ведущим двери с козой не несёт никакой информации о том, что находится за дверью, которую сначала выбрал игрок. Наиболее простой способ добиться этого — потребовать, чтобы в случае, когда автомобиль находится за дверью, выбранной игроком, ведущий открывал одну из оставшихся дверей с козами обязательно случайным образом.
Вначале вероятность того, что участник попадёт на автомобиль равна 1/3. После того как ведущий открывает дверь, большинство людей считают что она должна быть равна 1/2, но это не так. Ведущий знает, где находится автомобиль, и поэтому не открывает дверь с автомобилем. И вероятность была бы 1/2 только тогда, когда ведущий бы не знал положение призов, и тогда бы открытие двери ничего бы не меняло.
Наиболее существенным дополнением по сравнению с приведённой выше формулировкой здесь является то, что игрок до начала игры знает, что после его выбора ведущий в любом случае откроет дверь с козой и в любом случае предложит игроку изменить свой выбор, то есть совершение данных действий ведущим не несёт никакой информации о том, правильным или неправильным был первоначальный выбор игрока.
Решение
Правильным ответом к этой задаче является следующее: да, шансы выиграть автомобиль увеличиваются в два раза, если игрок будет следовать совету ведущего и изменит свой первоначальный выбор.
Наиболее простое объяснение этого ответа состоит в следующем соображении. Для того, чтобы выиграть автомобиль без изменения выбора, игрок должен сразу угадать дверь, за которой стоит автомобиль. Вероятность этого равна 1/3. Если же игрок первоначально попадает на дверь, за которой стоит коза (а вероятность этого события 2/3, поскольку есть две козы и лишь один автомобиль), то он может однозначно выиграть автомобиль, изменив своё решение, так как остаются автомобиль и одна коза, а дверь с козой ведущий уже открыл.
Таким образом, без смены выбора игрок остаётся при своей первоначальной вероятности выигрыша 1/3, а при смене первоначального выбора, игрок оборачивает себе на пользу в два раза большую оставшуюся вероятность того, что в начале он не угадал.
Также интуитивно понятное объяснение можно сделать, поменяв местами два события. Первое событие – принятие решения игроком о смене двери, второе событие – открытие лишней двери. Это допустимо, т.к. открытие лишней двери не дает игроку никакой новой информации (док-во см. в этой статье).
Тогда задачу можно свести к следующей формулировке. В первый момент времени игрок делит двери на две группы: в первой группе одна дверь (та что он выбрал), во второй группе две оставшиеся двери. В следующий момент времени игрок делает выбор между группами (sic!). Очевидно, что для первой группы вероятность выигрыша 1/3, для второй группы 2/3. Игрок выбирает вторую группу. Во второй группе он может открыть обе двери (sic!). Одну открывает ведущий, а вторую сам игрок.
Ключи к пониманию
Несмотря на простоту объяснения этого явления, множество людей интуитивно полагают, что вероятность выигрыша не меняется при изменении игроком своего выбора. Обычно невозможность изменения вероятности выигрыша мотивируется тем, что при вычислении вероятности происшедшие в прошлом события не имеют значения, как это происходит, например, при подбрасывании монетки — вероятность выпадения орла или решки не зависит от того, сколько раз до этого выпал орёл или решка. Поэтому многие считают, что в момент выбора игроком одной двери из двух уже не имеет значения, что в прошлом имел место выбор одной двери из трёх, и вероятность выиграть автомобиль одинаковая как при изменении выбора, так и при оставлении первоначального выбора.
Однако, хотя такие соображения верны в случае подбрасывания монетки, они верны не для всех игр. В данном случае должно быть проигнорировано открытие двери ведущим. Игрок по существу выбирает между той одной дверью, которую он выбрал сначала, и остальными двумя — открытие одной из них служит лишь для отвлечения внимания игрока. Известно, что имеется один автомобиль и две козы. Первоначальный выбор игроком одной из дверей делит возможные исходы игры на две группы: либо автомобиль находится за дверью, выбранной игроком (вероятность этого 1/3), либо за одной из двух других (вероятность этого 2/3). При этом уже известно, что в любом случае за одной из двух оставшихся дверей находится коза, и, открывая эту дверь, ведущий не даёт игроку никакой дополнительной информации о том, что находится за выбранной игроком дверью. Таким образом, открытие ведущим двери с козой не меняет вероятности (2/3) того, что автомобиль находится за одной из оставшихся дверей. А поскольку уже открытую дверь игрок не выберет, то вся эта вероятность оказывается сосредоточена в том событии, что автомобиль находится за оставшейся закрытой дверью.
Более интуитивно понятное рассуждение: Пусть игрок действует по стратегии «изменить выбор». Тогда проиграет он только в том случае, если изначально выберет автомобиль. А вероятность этого — одна треть. Следовательно, вероятность выигрыша: 1-1/3=2/3. Если же игрок действует по стратегии «не менять выбор», то он выиграет тогда и только тогда, когда изначально выбрал автомобиль. А вероятность этого — одна треть.
Другая частая причина трудного понимания решения этой задачи состоит в том, что нередко люди представляют себе немного другую игру — когда заранее неизвестно, будет ли ведущий открывать дверь с козой и предлагать игроку изменить свой выбор. В этом случае игрок не знает тактики ведущего (то есть, по существу, не знает всех правил игры) и не может сделать оптимальный выбор. Например, если ведущий будет предлагать смену варианта лишь в случае, когда игрок изначально выбрал дверь с автомобилем, то, очевидно, игрок должен всегда оставлять первоначальное решение без изменения. Именно поэтому важно иметь в виду точную формулировку задачи Монти Холла.(Хотя, даже при таком варианте, правильной стратегией будет смена выбора двери (при условии, что игрок не знает «хитрости» ведущего). Так как в этом случае проигрыш будет означать реализацию вероятности 1/3.)
Увеличение количества дверей
Для того, чтобы легче понять суть происходящего, можно рассмотреть случай, когда игрок видит перед собой не три двери, а, например, сто. При этом за одной из дверей находится автомобиль, а за остальными 99 — козы. Игрок выбирает одну из дверей, при этом в 99 % случаев он выберет дверь с козой, а шансы сразу выбрать дверь с автомобилем очень малы — они составляют 1 %. После этого ведущий открывает 98 дверей с козами и предлагает игроку выбрать оставшуюся дверь. При этом в 99 % случаев автомобиль будет находиться за этой оставшейся дверью, поскольку шансы на то, что игрок сразу выбрал правильную дверь, очень малы. Понятно, что в этой ситуации рационально мыслящий игрок должен всегда принимать предложение ведущего.
При рассмотрении увеличенного количества дверей нередко возникает вопрос: если в оригинальной задаче ведущий открывает одну дверь из трёх (то есть 1/3 от общего количества дверей), то почему нужно предполагать, что в случае 100 дверей ведущий откроет 98 дверей с козами, а не 33 ? Это соображение является обычно одной из существенных причин того, почему парадокс Монти Холла входит в противоречие с интуитивным восприятием ситуации. Предполагать открытие 98 дверей будет правильным потому, что существенным условием задачи является наличие только одного альтернативного варианта выбора для игрока, который и предлагается ведущим. Поэтому для того, чтобы задачи были аналогичными, в случае 4 дверей ведущий должен открывать 2 двери, в случае 5 дверей — 3, и так далее, чтобы всегда оставалась одна неоткрытая дверь кроме той, которую изначально выбрал игрок. Если ведущий будет открывать меньшее количество дверей, то задача уже не будет аналогична оригинальной задаче Монти Холла.
Следует отметить, что в случае множества дверей, даже если ведущий будет оставлять закрытой не одну дверь, а несколько, и предлагать игроку выбрать одну из них, то при смене первоначального выбора шансы игрока выиграть автомобиль всё равно будут увеличиваться, хотя и не столь значительно. Например, рассмотрим ситуацию, когда игрок выбирает одну дверь из ста, и затем ведущий открывает только одну дверь из оставшихся, предлагая игроку изменить свой выбор. При этом шансы на то, что автомобиль находится за первоначально выбранной игроком дверью, остаются прежними — 1/100, а для остальных дверей шансы изменяются: суммарная вероятность того, что автомобиль находится за одной из оставшихся дверей (99/100) распределяется теперь не на 99 дверей, а на 98. Поэтому вероятность нахождения автомобиля за каждой из этих дверей будет равна не 1/100, а 99/9800. Прирост вероятности составит примерно 0.01 %.
Дерево принятия решений
 Дерево возможных решений игрока и ведущего, показывающее вероятность каждого исхода
Дерево возможных решений игрока и ведущего, показывающее вероятность каждого исходаБолее формально сценарий игры может быть описан c помощью дерева принятия решений.
В первых двух случаях, когда игрок сначала выбрал дверь, за которой находится коза, изменение выбора приводит к выигрышу. В двух последних случаях, когда игрок сначала выбрал дверь с автомобилем, изменение выбора приводит к проигрышу.
Суммарная вероятность того, что изменение выбора приведёт к выигрышу, эквивалентна сумме вероятностей первых двух исходов, то есть
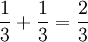 . Соответственно, вероятность того, что отказ от изменения выбора приведёт к выигрышу, равна
. Соответственно, вероятность того, что отказ от изменения выбора приведёт к выигрышу, равна 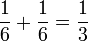 .
.Проведение похожего эксперимента
Существует простой способ убедиться в том, что изменение первоначального выбора приводит к выигрышу в двух случаях из трёх в среднем. Для этого можно сымитировать игру, описанную в задаче Монти Холла, с помощью игральных карт. Один человек (раздающий карты) при этом играет роль ведущего Монти Холла, а второй — роль игрока. Для игры берутся три карты, из которых одна изображает дверь с автомобилем (например, туз пик), а две других, одинаковых (например, две красные двойки) — двери с козами.
Ведущий выкладывает три карты рубашкой вверх, предлагая игроку взять одну из карт. После того, как игрок выберет карту, ведущий смотрит в две оставшиеся карты и открывает красную двойку. После этого открываются карты, оставшиеся у игрока и у ведущего, и если выбранная игроком карта — туз пик, то записывается очко в пользу варианта, когда игрок не меняет свой выбор, а если у игрока оказывается красная двойка, а у ведущего остаётся туз пик, то записывается очко в пользу варианта, когда игрок меняет свой выбор. Если провести множество таких раундов игры, то соотношение между очками в пользу двух вариантов достаточно хорошо отразит соотношение вероятностей этих вариантов. При этом оказывается, что число очков в пользу смены первоначального выбора примерно в два раза больше.
Такой эксперимент позволяет не только убедиться в том, что вероятность выигрыша при изменении выбора в два раза больше, но и хорошо иллюстрирует, почему так происходит. В тот момент, когда игрок выбрал себе карту, уже определено, находится ли в его руке туз пик или нет. Дальнейшее открытие ведущим одной из своих карт не меняет ситуации — игрок уже держит карту в руке, и она остаётся там независимо от действий ведущего. Вероятность же для игрока выбрать туз пик из трёх карт равна, очевидно, 1/3, и, таким образом, вероятность его не выбрать (и тогда игрок выиграет, если изменит первоначальный выбор) равна 2/3.
Доказательство с помощью таблицы
При проведении большого числа экспериментов машина должна обнаруживаться за каждой из дверей одинаковое количество раз, то есть очень близко к 1/3 от общего количества.
дверь 1 дверь 2 дверь 3 Выбор Машина Коза Открыта коза Выбор Машина Открыта коза Выбор Открыта коза Машина По законам распределения вероятности вы выберете неправильную дверь в 2 случаях из 3. Это означает, что в 2 из 3 случаев вы получите машину просто изменив решение. Таблица показывает, что вы, скорее всего, ошибётесь при первом выборе и в этом случае вы попадаете в две другие строки таблицы. А здесь уже вам покажут, какую дверь нужно выбрать.
Проблема трёх заключенных
Другая формулировка парадокса была представлена Мартином Гарднером в колонке Математические игры, которую он вёл в журнале Scientific American, в 1959.
Трое заключенных A, B и C приговорены к смертной казни, однако известно что один будет помилован. Приговор запрещает сообщать преступнику, будет ли он помилован или нет. A уговаривает охранника сказать, кого из двух других заключенных казнят. Так как вопрос не касается A, охранник решается сообщить, что казнят B. Как изменились вероятности казни A и C? Или, проводя аналогию с проблемой Монти Холла, следует ли A поменяться местами с С, если у него есть такая возможность?
Ответ
В таблице приведены вероятности того, кто из заключенных будет помилован, до и после сообщения охранника.
До сообщения охранника После сообщения охранника - p(A) = 1/3
- p(B) = 1/3
- p(C) = 1/3
- p(A) = 1/3
- p(B) = 0
- p(C) = 2/3
Таким образом, A делает заключение о том, что C имеет вдвое более высокую вероятность выжить по сравнению с ним. Поэтому, если есть возможность, ему следует поменяться с C
Ключом к пониманию ответа является то, что охранник не сообщает A новой информации о его судьбе, так как A и до сообщения охранника знал о том, что его либо помилуют, либо нет, а хотя бы один из двух других заключенных будет казнён. О судьбе заключенных B и C заявление охранника, конечно, несет информацию (предполагается, что охранник сказал правду). Вероятность того, что помилуют B, становится равна нулю, а вероятность того, что помилуют C, увеличивается. Несимметричность значений вероятности быть казненным для A по сравнению с C объясняется тем, что охранник поделился информацией именно с A.
Эту задачу можно свести к более простой задаче, и её моделирование будет очень простым:
1 стратегия: если мы не меняем выбор, то независимо от того, какую дверь открыл ведущий, мы выигрываем только тогда, когда сразу и точно угадали дверь. Другими словами, мы выиграли — если загаданный номер двери ведущего совпадает с номером двери, которую выбрали мы.
2 стратегия: если же мы меняем выбор, то всё становится наоборот: мы проигрываем, если сразу угадали дверь, но поменяли её. И выигрываем, если сразу не угадали дверь, но изменили её на дверь ведущего.Получается, что для подсчёта выигрышей по первой стратегии достаточно считать только случаи, когда мы точно угадали, загаданный ведущим, номер двери. А выигрыши по второй стратегии — это проирыши по первой.
См. также
- Условная вероятность
- Теорема Байеса
- Проблема трёх заключённых (англ.)
Ссылки
- Объясняющий видеоролик на сайте Smart Videos .ru
- Статья в газете «Дуэль» о парадоксе Монти Холла
- Weisstein, Eric W. Парадокс Монти Холла на сайте Wolfram MathWorld.(англ.)
- Парадокс Монти Холла на сайте телешоу Let’s Make a deal
- Отрывок из книги С.Лукьяненко, в котором используется парадокс Монти Холла
Литература
- vos Savant, Marilyn. Колонка «Ask Marilyn», журнал Parade Magazine от 17 февраля 1990.
- vos Savant, Marilyn. Колонка «Ask Marilyn», журнал Parade Magazine от 26 февраля 2006.
- Bapeswara Rao, V. V. and Rao, M. Bhaskara. «A three-door game show and some of its variants». Журнал The Mathematical Scientist, 1992, № 2.
- Tijms, Henk. Understanding Probability, Chance Rules in Everyday Life. Cambridge University Press, New York, 2004. (ISBN 0-521-54036-4)
Wikimedia Foundation. 2010.
