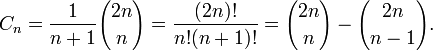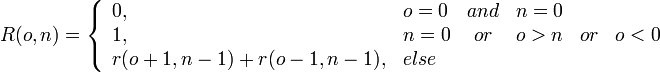- Правильная скобочная структура
-
Пра́вильная ско́бочная после́довательность(ПСП) - частный случай скобочной последовательности. Формально определяется следующим образом:
-
- "" (пустая строка) - ПСП
- ПСП, взятая в скобки одного типа - ПСП
- ПСП, к которой приписана слева или справа ПСП - тоже ПСП
Подсчёт количества правильных скобочных последовательностей
Первым, что должно заинтересовать читателя, является число возможных способов составить правильные скобочные последовательности из 2n скобок (n открывающих и n закрывающих). Для определения этого количества для скобочных последовательностей с одним типом скобок существует несколько формул. Широко распространены следующие две:
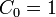 и
и 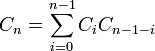 для
для 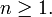
Это соотношение легко получить, заметив, что любая непустая правильная скобочная последовательность ω однозначно представима в форме ω = (ω1)ω2, где ω1,2 — правильные скобочные последовательности.
- Выражение через биномиальные коэффициенты:
Помимо уже приведённых есть ещё одна формула, определённая ниже:
Для получения Cn достаточно вычислить R(0,2n).
Особенности этой функции, её дополнительные применения и строгий вывод будут рассмотрены далее, в разделе генерация скобочных последовательностей. Легко показать, что если в скобочной последовательности имеется k типов скобок, то количество возможных правильных скобочных последовательностей с n открывающими скобками равно произведению Cn на kn. Действительно, для каждой открывающей скобки из n существует k различных вариантов её выбора. Выбор закрывающей скобки однозначно определён уже выбранной парной ей открывающей и не учитывается.
Генерация правильных скобочных последовательностей
Введём теперь лексикографический порядок на скобочных последовательностях. В первую очередь заметим, что открывающая скобка идёт раньше, чем закрывающая; так как скобочная последовательность, начинающаяся с закрывающей скобки, не является правильной. Теперь каждому из k типов скобок присвоим свой лексикографический приоритет. Выбор этого приоритета не принципиален и ни на что не повлияет в ходе дальнейших рассуждений. Поэтому будем считать, что iй тип скобок находится на iй позиции в лексикографическом порядке. Очевидно, что первой последовательностьтью с n открывающими скобками будет последовательность вида (1(1...(1)1)1...)1. Теперь рассмотрим задачу о получении следующей скобочной последовательности после данной.
Получение следующей правильной скобочной последовательности
-
Wikimedia Foundation. 2010.