- Правило Коновалова
-
Законы Коновалова описывают процессы, протекающие в равновесных системах "жидкий раствор - пар" под действием температуры или давления.
Содержание
Первый закон Коновалова
Первый закон Коновалова (1881 г.) описывает процесс фракционной перегонки:
- насыщеный пар по сравнению с равновесным раствором обогащён компонентом, добавление которого к системе повышает общее давление пара
Рассмотрим фазовую диаграмму при постоянном давлении для бинарной системы в координатах состав - температура:
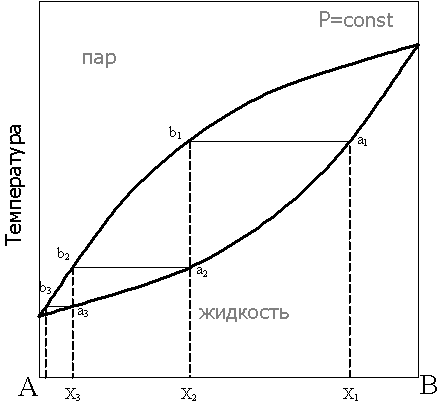
При нагревании исходной смеси состава Х1 кипение начнётся в точке а1. При этом состав первых порций пара соответствует точке b1. При конденсации этого пара образуется смесь состава Х2, в которой доля компонента А выше, по сравнению с исходной смесью. Нагрев этой смеси приведёт к получению конденсата состава Х3 и так далее, вплоть до выделения чистого компонента А. Отметим, что при кипении смеси состава Х1 состав жидкости будет обогащаться компонентом В, соответственно температура кипящей жидкости будет повышаться до тех пор, пока в жидкости не останется только компонент В. Последовательные перегонки в промышленных условиях объединены в один автоматизированный процесс в дефлегмационных и ректификационных колоннах.
Второй закон Коновалова
Второй закон Коновалова (1881 г.) описывает растворы с отклонениями от свойств идеальных растворов и объясняет существование азеотропных растворов, состав которых при перегонке не изменяется:
- Экстремумы на кривых полного давления пара отвечают такому равновесию раствора и насыщенного пара, при котором состав обеих фаз одинаков
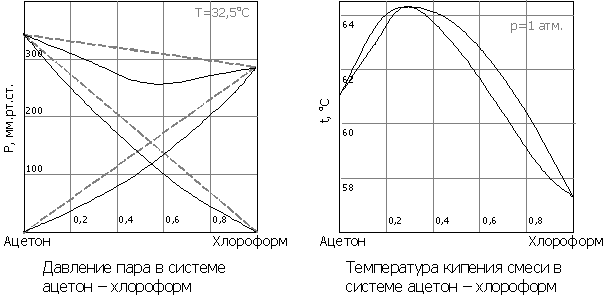
Доказательство второго закона Коновалова
Согласно уравнению Дюгема-Маргулеса, которое описывает равновесие в идеальных бинарных растворах газов или давление насыщенного пара над идеальным бинарным жидким раствором
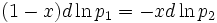 или
или 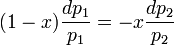
, где
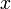 - мольная доля второго компонента в растворе,
- мольная доля второго компонента в растворе, 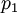 и
и 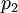 - парциальные давления первого и второго компонента.
- парциальные давления первого и второго компонента.Отсюда следует, что
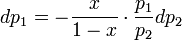
По закону Дальтона
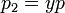
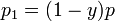
где
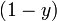 и
и 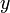 - мольные доли первого и второго компонента в насыщенном паре,
- мольные доли первого и второго компонента в насыщенном паре, 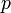 - общее давление в системе. Тогда
- общее давление в системе. Тогда 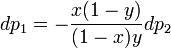
Поскольку общее давление есть сумма парциальных, то
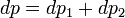 . Подставив в это выражение значение
. Подставив в это выражение значение 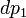 из предыдущего получим
из предыдущего получим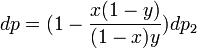
Разделив обе части на
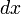 и раскрыв скобки получим, что
и раскрыв скобки получим, что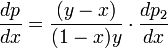
В экстремуме
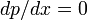 , следовательно
, следовательно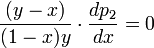
Поскольку
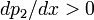 , т.к. с ростом концентрации второго компонента растёт и его парциальное давление, то равенство может соблюдаться только если
, т.к. с ростом концентрации второго компонента растёт и его парциальное давление, то равенство может соблюдаться только если 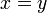 - когда состав пара и раствора одинаков, что и доказывает второй закон Коновалова. Растворы, состав которых отвечает точке экстремума, кипят при постоянной температуре, а их состав при перегонке не изменяется. Такие растворы называются "азеотропными растворами" или "азеотропами". Разделение азеотропов методом фракционной перегонки невозможно. Для разделения таких растворов используют химические методы, перегонку с третьим компонентом либо фракционная перегодка при другом давлении.
- когда состав пара и раствора одинаков, что и доказывает второй закон Коновалова. Растворы, состав которых отвечает точке экстремума, кипят при постоянной температуре, а их состав при перегонке не изменяется. Такие растворы называются "азеотропными растворами" или "азеотропами". Разделение азеотропов методом фракционной перегонки невозможно. Для разделения таких растворов используют химические методы, перегонку с третьим компонентом либо фракционная перегодка при другом давлении.Литература
- Герасимов Я.И и др. Курс физической химии М.:Химия, 1970 г.
См. также
Wikimedia Foundation. 2010.
