Определитель Вронского

Вронскиа́н (определитель Вронского) системы функций 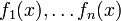$f_1(x),\ldots f_n(x)$, дифференцируемых на промежутке I (n-1)-раз — функция на I, задаваемая определителем следующей матрицы:

$W(f_1,\dots f_n)(x) = \det\begin{pmatrix} f_1(x) & f_2(x) &\cdots & f_n(x) \\ f'_1(x) & f'_2(x) & \cdots & f'_n(x) \\ \vdots & \vdots & \ddots & \vdots \\ f_1^{(n-1)}(x) & f_2^{(n-1)}(x) & \cdots & f_n^{(n-1)}(x) \end{pmatrix};\qquad x\in I,$.

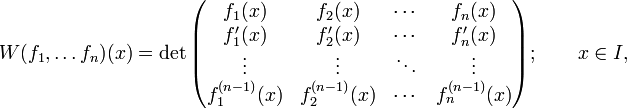Также вронскианом называют функцию, заданную определителем более общего вида. А именно, пусть задано n вектор-функций 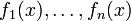$f_1(x), \ldots , f_n(x)$ с n компонентами: 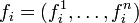$f_i=(f_i^1, \ldots ,f_i^n)$. Тогда определитель будет выглядеть так (чтобы избежать разночтений обозначим его W₂):

$W_2(f_1,\dots f_n)(x) = \det\begin{pmatrix} f_1^1(x) & f_2^1(x) &\cdots & f_n^1(x) \\ f_1^2(x) & f_2^2(x) & \cdots & f_n^2(x) \\ \vdots & \vdots & \ddots & \vdots \\ f_1^n(x) & f_2^n(x) & \cdots & f_n^n(x) \end{pmatrix};\qquad x\in I,$.

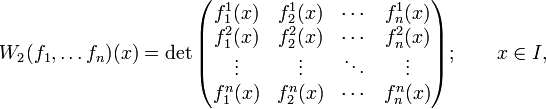Определитель Вронского применяется для решения дифференциальных уравнений, например для того, чтобы узнать, являются ли найденные решения однородного линейного дифференциального уравнения (либо системы уравнений) линейно независимыми. Это помогает в поиске его общего решения.