Метод Штрассена

Если перед нами стоит задача получить произведение C двух матриц A и B размера n×n, то это можно сделать несколькими способами. Лобовой алгоритм, умножающий по формуле c_ik = Σa_ijb_jk, работает за время Θ(n³) = Θ(n^{log₂ 8}). Другой простой алгоритм работает рекурсивно и разбивает каждую из умножаемых матриц на 4 части так, что произведение C = AB представимо следующим образом:

$\begin{pmatrix} r & s \\ t & u \end{pmatrix} = \begin{pmatrix} a & b \\ c & d \end{pmatrix}\begin{pmatrix} e & g \\ f & h \end{pmatrix} \begin{matrix}& & r = ae + bf & t= ce + df \\ \ & & s = ag + bh & u= cg + dh\end{matrix}$

Он производит 8 умножений матриц размером 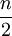$n \over 2$, поэтому также работает за время Θ(n^{log₂ 8}). Алгоритм Штрассена, обозначает схему, при которой в рекурсивном алгоритме можно обойтись семью умножениями матриц размера 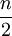$n \over 2$, тем самым сократив трудоемкость до Θ(n^{log₂ 7}) = Θ(n^2.81), что дает заметный выигрыш на больших плотных матрицах (начиная, примерно, от 64×64).

Описание алгоритма

Вначале мы проверяем, является ли размер умножаемых матриц n натуральной степенью двойки. Если нет, мы дополняем исходные матрицы дополнительными нулевыми строками и столбцами. При этом мы получаем удобные для рекурсивного умножения размеры, но теряем в эффективности за счет дополнительных ненужных умножений. Алгоритм Штрассена умножает две (n×n)-матрицы A и B следующим образом:

1. Каждая из матриц A и B разбивается на 4 блока по схеме, приведенной выше.
2. Строятся 14 матриц A₁, B₁, A₂, B₂, …, A₇, B₇ размера (n/2×n⁄2) (для чего нужно Θ(n²) операций сложения/вычитания чисел).
3. Рекурсивно вычисляются 7 произведений матриц меньшего размера P_i = A_iB_i (i = 1, …, 7).
4. Вычисляются части r, s, t, u искомой матрицы C. Они являются линейными комбинациями матриц P_i с коэффициентами из множества {−1, 0, 1}, и вычисление их требует Θ(n²) операций сложения/вычитания чисел.

Формулы, по которым происходит умножение

i	Ai	Bi	Pi = AiBi
1	a	f - h	af - ah
2	a + b	h	ah + bh
3	c + d	e	ce + de
4	d	g − e	dg − de
5	a + d	e + h	ae + ah + de + dh
6	b − d	g + h	bg + bh − dg − dh
7	a − c	e + f	ae + af − ce − cf

r = P₅ + P₄ − P₂ + P₆ = ae + bf
s = P₁ + P₂ = ag + bh
t = P₃ + P₄ = ce + df
u = P₅ + P₁ − P₃ − P₇ = cg + dh

Тем не менее, самый асимптотически быстрый из известных на сегодняшний день способ умножения матриц был опубликован Копперсмитом и Виноградом в 1987-м году и позволяет перемножать квадратные матрицы за время Θ(n^2.38). На практике же метод Штрассена гораздо проще программируется и имеет меньшую константу в оценке трудоемкости.

Литература

• Ананий В. Левитин Глава 4. Метод декомпозиции: Умножение больших целых чисел и алгоритм умножения матриц Штрассена // Алгоритмы: введение в разработку и анализ = Introduction to The Design and Analysis of Aigorithms. — М.: «Вильямс», 2006. — С. 189-195. — ISBN 0-201-74395-7

• Кормен, Томас Х., Лейзерсон, Чарльз И., Ривест, Рональд Л., Штайн, Клифорд Глава 28. Работа с матрицами // Алгоритмы: построение и анализ = Introduction to Algorithms. — 2-e издание. — М.: «Вильямс», 2005. — С. 833 - 839. — ISBN 5-8459-0857-4