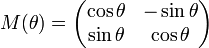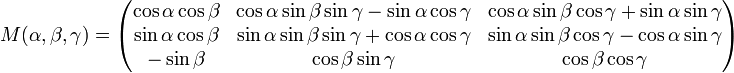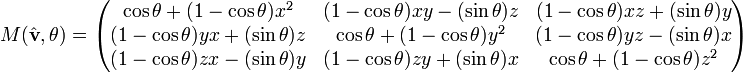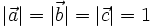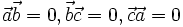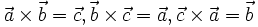Матрица вращения

Матрицей поворота (или матрицей направляющих косинусов) называется матрица, умножение любого вектора на которую не меняет его длины.

Матрица поворота в двумерном пространстве

В двумерном пространстве поворот можно описать одним углом θ. Положительным углам соответствует вращение против часовой стрелки.

Матрица поворота вектора в декартовой системе координат:

$M(\theta) = \begin{pmatrix} \cos{\theta} & -\sin{\theta} \\ \sin{\theta} & \cos{\theta} \end{pmatrix}$

Сам поворот происходит путём умножения вектора (описывающего вращаемую точку) на матрицу:

$\vec{p\,}' = M\cdot \vec p$.

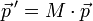Матрица поворота в трёхмерном пространстве

Матрицами вращения вокруг оси декартовой правосторонней системы координат на угол α в трёхмерном пространстве являются:

• Вращение вокруг оси x:

$\begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha \\ 0 & \sin \alpha & \cos \alpha \end{pmatrix}$,

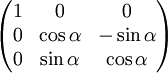• Вращение вокруг оси y:

$\begin{pmatrix} \cos \alpha & 0 & \sin \alpha \\ 0 & 1 & 0 \\ -\sin \alpha & 0 & \cos \alpha \end{pmatrix}$,

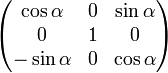• Вращение вокруг оси z:

$\begin{pmatrix} \cos \alpha & -\sin \alpha & 0 \\ \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 1 \end{pmatrix}$,

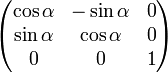В трёхмерном пространстве для описания поворота можно использовать

• матрицу поворота 3x3,
• три угла, например, углы Эйлера (γ,β,α),
• угол поворота θ и единичный вектор оси вращения $\hat{\mathbf{v}} = (x,y,z)$,
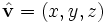• кватернион.

Матрицы поворота вектора в декартовой системе координат, соответствующие этим двум способам задания поворота:

$M(\alpha,\beta,\gamma) = \begin{pmatrix} \cos \alpha \cos \beta & \cos \alpha \sin \beta \sin \gamma - \sin \alpha \cos \gamma & \cos \alpha \sin \beta \cos \gamma + \sin \alpha \sin \gamma \\ \sin \alpha \cos \beta & \sin \alpha \sin \beta \sin \gamma + \cos \alpha \cos \gamma & \sin \alpha \sin \beta \cos \gamma - \cos \alpha \sin \gamma \\ - \sin \beta & \cos \beta \sin \gamma & \cos \beta \cos \gamma \end{pmatrix}$

и

$M(\hat{\mathbf{v}},\theta) = \begin{pmatrix} \cos \theta + (1 - \cos \theta) x^2 & (1 - \cos \theta) x y - (\sin \theta) z & (1 - \cos \theta) x z + (\sin \theta) y \\ (1 - \cos \theta) y x + (\sin \theta) z & \cos \theta + (1 - \cos \theta) y^2 & (1 - \cos \theta) y z - (\sin \theta) x \\ (1 - \cos \theta) z x - (\sin \theta) y & (1 - \cos \theta) z y + (\sin \theta) x & \cos \theta + (1 - \cos \theta) z^2 \end{pmatrix}$

Свойства матрицы поворота

Если 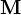$\mathbf{M}$ — матрица, задающая поворот вокруг оси 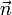$\vec n$ на угол φ, то: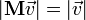

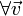
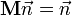
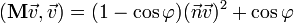
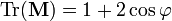• $|\mathbf{M} \vec v| = |\vec v|$ $\forall \vec v$
• $\mathbf{M} \vec n = \vec n$
• $(\mathbf{M} \vec v,\vec v) = (1-\cos\varphi)(\vec n \vec v)^2+\cos\varphi$
• $\operatorname{Tr}(\mathbf{M}) = 1 + 2 \cos\varphi$ (след матрицы вращения)
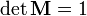• $\det \mathbf{M} = 1$ (матрица имеет единичный определитель).
• если строки (или столбцы матрицы) рассматривать как координаты векторов 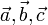$\vec a, \vec b, \vec c$, то верны следующие соотношения):
  • $|\vec a| = |\vec b| = |\vec c| = 1$
  • $\vec a \vec b = 0, \vec b \vec c = 0, \vec c \vec a = 0$
  • $\vec a \times \vec b = \vec c, \vec b \times \vec c = \vec a, \vec c \times \vec a = \vec b$
• Матрица обратного поворота получается обычным транспонированием матрицы прямого поворота, т.о. $\mathbf{M}^\mathrm{-1} = \mathbf{M}^\mathrm{T}$.

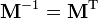См. также

• Матрица перехода

Литература

• Лурье А. И. Аналитическая механика — М.:Физматлит — 1961 г. — 824 с.

Ссылки

• Поворот плоскости. Матрица поворота