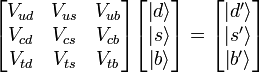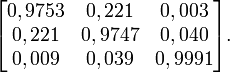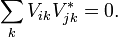Матрица Кобаяси – Маскава

Аромат в физике элементарных частиц

Ароматы и квантовые числа: Лептонное число: L Барионное число: B Странность: S Очарование: C Прелесть: B' Истинность: T Изоспин: I или Iz Слабый изоспин: Tz Электрический заряд: Q Комбинации: Гиперзаряд: Y Y=2(Q-Iz) Y=B+S+C+B'+T Слабый гиперзаряд: YW YW=2(Q-Tz) YW=B−L См. также: CPT-инвариантность CKM-матрица CP-инвариантность Хиральность

CKM-ма́трица, ма́трица Каби́ббо-Кобая́ши-Маска́вы (ККМ-матрица, матрица смешивания кварков, иногда раньше называлась KM-матрица) в Стандартной модели физики элементарных частиц — унитарная матрица, которая содержит информацию о силе слабых распадов, изменяющих аромат. Технически, она определяет преобразование между двумя базисами квантовых состояний: состояниями свободно движущихся кварков (т.е. их массовыми состояниями) и состояниями кварков, участвующих в слабых взаимодействиях (т.е. их флейворными состояниями). Она важна также для понимания нарушения CP-симметрии. Точное математическое определение этой матрицы дано в статье по основам Стандартной модели. Эта матрица была предложена для трёх поколений кварков японскими физиками Макото Кобаяси и Тосихидэ Масукава, которые добавили одно поколение к матрице, ранее предложенной Николой Кабиббо.

Матрица

$\begin{bmatrix} V_{ud} & V_{us} & V_{ub} \\ V_{cd} & V_{cs} & V_{cb} \\ V_{td} & V_{ts} & V_{tb} \end{bmatrix} \begin{bmatrix} \left| d \right \rangle \\ \left| s \right \rangle \\ \left| b \right \rangle \end{bmatrix} = \begin{bmatrix} \left| d' \right \rangle \\ \left| s' \right \rangle \\ \left| b' \right \rangle \end{bmatrix}$

Слева мы видим CKM-матрицу вместе с вектором сильных собственных состояний кварков, а справа имеем слабые собственные состояния кварков. ККМ матрица описывает вероятность перехода от одного кварка q к другому кварку q' . Эта вероятность пропорциональна $\left| V_{qq'} \right| ^2$.

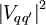Величины значений в матрице были установлены экспериментально и равны приблизительно:

$\begin{bmatrix} 0,9753 & 0,221 & 0,003 \\ 0,221 & 0,9747 & 0,040 \\ 0,009 & 0,039 & 0,9991 \end{bmatrix}.$

Таким образом, CKM-матрица довольно близка к единичной матрице.

Подсчёт

Чтобы идти дальше, необходимо подсчитать количество параметров в этой матрице V, которые проявляются в экспериментах и, следовательно, физически важны. Если есть N поколений кварков (2N ароматов), то

1. комплексная матрица N×N содержит 2N² действительных чисел.
2. Ограничивающее условие унитарности ∑_k V_ikV ^*_jk = δ_ij. Следовательно, для диагональных компонент (i=j) существует N ограничений, а для остающихся компонент — N(N−1). Количество независимых действительных чисел в унитарной матрице равно N².
3. Одна фаза может быть поглощена каждым кварковым полем. Общая фаза ненаблюдаема. Следовательно, количество независимых чисел уменьшается на 2N−1, то есть общее количество свободных переменных равно (N²−2N+1)=(N−1)².
4. Из них N(N−1)/2 — углы вращения, называемые кварковыми углами смешивания.
5. Оставшиеся (N−1)(N−2)/2 являются комплексными фазами, вызывающими нарушение CP-инвариантности.

Если число поколений кварков N=2 (исторически такой была первая версия CKM-матрицы, когда были известны только два поколения), есть только один параметр — угол смешивания между двумя поколениями кварков. Он называется угол Кабиббо в честь Николы Кабиббо.

В Стандартной модели N=3, следовательно, есть три угла смешивания и одна комплексная фаза, нарушающая CP-симметрию.

Наблюдения и предсказания

Идея Кабиббо появилась из-за необходимости объяснения двух наблюдаемых явлений:

1. переходы u↔d и e↔ν_e, μ↔ν_μ имели похожие амплитуды.
2. переходы с изменением странности ΔS=1 имели амплитуды, равные 1/4 от амплитуд переходов без изменения странности (ΔS=0).

Решение Кабиббо состояло в постулировании универсальности слабых переходов, чтобы решить проблему 1, и угла смешивания θ_c (теперь называемого углом Кабиббо) между d- и s-кварками, чтобы решить проблему 2.

Для двух поколений кварков нет нарушающей CP-симметрию фазы, как было показано выше. Поскольку нарушение CP-симметрии наблюдалось в распадах нейтральных каонов уже в 1964 г., появление немногим позже Стандартной модели было ясным сигналом о третьем поколении кварков, как было указано в 1973 г. Кобаяси и Масукавой. Открытие b-кварка в Фермилабе (группой Леона Ледермана) в 1977 г. немедленно привело к началу поисков еще одного кварка третьего поколения — t-кварка.

Универсальность слабых переходов

Ограничение по унитарности CKM-матрицы для диагональных компонент может быть записано как

∑	| Vij | 2 = 1
j

для всех поколений i. Это предполагает, что сумма всех связей кварка u-типа со всеми кварками d-типа одинакова для всех поколений. Никола Кабиббо в 1967 г. назвал это соотношение слабой универсальностью. Теоретически, это следствие того факта, что все дублеты SU(2) взаимодействуют с векторными бозонами слабых взаимодействий с одинаковой константой связи. Это подтверждено во многих экспериментах.

Треугольники унитарности

Оставшиеся ограничения по унитарности ККМ матрицы могут быть записаны в форме

$\sum_k V_{ik}V^*_{jk} = 0.$

Для любых фиксированных и различных i и j это ограничение накладывается на три комплексных числа, одно для каждого k, что означает, что эти числа являются вершинами треугольника на комплексной плоскости. Существует шесть вариантов i и j, поэтому и шесть таких треугольников, каждый из которых называется треугольником унитарности. Их формы могут быть очень разными, но они все имеют одинаковую площадь, которую можно отнести к нарушающей CP-симметрию фазе. Площадь исчезает для специфических параметров в Стандартной модели, для которых нет нарушения CP-симметрии. Ориентация треугольников зависит от фаз кварковых полей.

Поскольку как три стороны, как и три угла каждого треугольника могут быть измерены в прямых экспериментах, проводится серия тестов для проверки замкнутости треугольников. Это задача для таких экспериментов, как японский BELLE, калифорнийский LHC.

См. также

• Стандартная модель (основы) и нарушение CP-инвариантности.
• Квантовая хромодинамика, аромат и сильная CP-проблема.
• МНС матрица, эквивалентная матрица смешивания для нейтрино.

Ссылки

• Introduction to Elementary Particles. — Wiley, John & Sons, Inc, 1987. — ISBN ISBN 0-471-60386-4
• Povh, Bogdan et al., (1995). Particles and Nuclei: An Introduction to the Physical Concepts. New York: Springer. ISBN 3-540-20168-8

Внешние ссылки

• CP violation, by I.I. Bigi and A.I. Sanda (Cambridge University Press, 2000) [ISBN 0-521-44349-0]
• Particle Data Group on CP violation
• The Babar experiment at SLAC and the BELLE experiment at KEK Japan
• N. Cabibbo, Phys. Rev. Lett. 10 (1963) 531.
• M. Kobayashi and K. Maskawa, Prog. Theor. Phys. 49 (1973) 652.