- Логическое умножение
-
Конъю́нкция — логическая операция, по своему применению максимально приближенная к союзу "и". Синонимы: логи́ческое "И", логи́ческое умноже́ние, иногда просто "И".
Это бинарная инфиксная операция, то есть, она имеет два операнда и ставится между ними. Чаще всего встречаются следующие варианты записи:
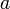 &&
&& 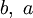 &
& 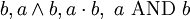 .
.
По аналогии с умножением в алгебре знак логического умножения может быть пропущен: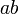 .
.Содержание
Булева алгебра
В булевой алгебре конъюнкция - это функция двух переменных (они же - операнды операции). Переменные могут принимать значения из множества
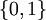 . Результат также принадлежит множеству
. Результат также принадлежит множеству 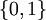 . Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений
. Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений 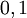 может использоваться любая другая пара подходящих символов, например
может использоваться любая другая пара подходящих символов, например 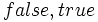 или
или 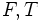 или "ложь", "истина".
или "ложь", "истина".Правило: результат равен
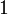 , если оба операнда равны
, если оба операнда равны 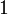 ; во всех остальных случаях результат равен
; во всех остальных случаях результат равен 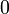 .
.Таблица истинности:
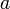

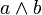
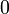
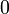
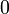
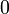
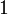
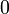
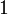
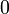
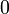
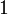
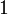
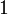
Многозначная логика
В многозначной логике операция конъюнкции может определяться другими способами. Чаще всего применяется схема:
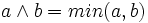 , где
, где ![~a, b \in [0, 1]](/pictures/wiki/files/100/dfbf391a6408e74c7a9b40da50e8fffd.png) . Возможны и другие варианты. Как правило, стараются сохранить совместимость с булевой алгеброй для значений операндов
. Возможны и другие варианты. Как правило, стараются сохранить совместимость с булевой алгеброй для значений операндовКлассическая логика
В классическом исчислении высказываний свойства конъюнкции определяются с помощью аксиом. Классическое исчисление высказываний может быть задано разными системами аксиом, и некоторые из них будут описывать свойства конъюнкции. Один из самых распространённых вариантов включает 3 аксиомы для конъюнкции:
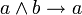
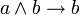
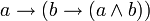
С помощью этих аксиом можно доказать другие формулы, содержащие операцию конъюнкции. Обратите внимание, что в классическом исчислении высказываний не происходит вычисления результата по значениям операндов (как в булевой алгебре), а требуется доказать формулу как единое целое на основе аксиом и правил вывода.
Программирование
В компьютерных языках используется два основных варианта конъюнкции: логическое "И" и побитовое "И". Например, в языках C/C++ логическое "И" обозначается символом "&&", а побитовое - символом "&".
Логическое "И" применяется в операторах условного перехода или в аналогичных случаях, когда требуется получение результата
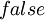 или
или 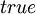 . Например:
. Например:if (a && b) { /* какие-то действия */ };
Результат будет равен
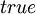 , если оба операнда равны
, если оба операнда равны 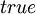 (для числовых типов не равны
(для числовых типов не равны 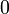 ). В любом другом случае результат будет равен
). В любом другом случае результат будет равен 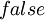 .
.При этом применяется стандартное соглашение: если значение левого операнда равно
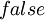 , то значение правого операнда не вычисляется (вместо
, то значение правого операнда не вычисляется (вместо  может стоять сложная формула). Такое соглашение ускоряет исполнение программы и служит полезным приемом в некоторых случаях. Например, если левый операнд проверяет возможность вычисления правого операнда:
может стоять сложная формула). Такое соглашение ускоряет исполнение программы и служит полезным приемом в некоторых случаях. Например, если левый операнд проверяет возможность вычисления правого операнда:if (a != 0 && b / a > 3) { /* какие-то действия */ };
В этом примере, благодаря проверке в левом операнде, в правом операнде никогда не произойдет деления на ноль.
Побитовое "И" выполняет обычную операцию булевой алгебры для всех битов левого и правого операнда попарно. Например,
если a = 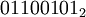
b = 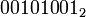
то a И b = 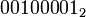
Связь с естественным языком
Часто указывают на сходство между конъюнкцией и союзом "и" в естественном языке. Составное утверждение "A и B" считается истинным, когда истинны оба утверждения A и B, в противном случае составное утверждение ложно. Это в точности соответствует определению конъюнкции в булевой алгебре, если "истину" обозначать как 1, а "ложь" как 0. При этом часто делают стандартную оговорку о неоднозначности естественного языка. Например, в зависимости от контекста союз "и" может нести дополнительный оттенок "и тогда", "и поэтому", "и потом"..."И" также несет в себе оттенок неопределенного смысла. Отличие логики естественного языка от математической остроумно выразил американский математик Стивен Клини, заметив, что в естественном языке "Мэри вышла замуж и родила ребенка" - не то же самое, что "Мэри родила ребенка и вышла замуж".
См. также
Wikimedia Foundation. 2010.
