Логический сдвиг

Би́товый сдвиг — изменение позиций битов в слове на одну и ту же величину.

В основной своей массе компьютеры не могут напрямую адресовать биты, которые содержатся группами по 8, 16, 32 битов в словах. Для обеспечения работы с битами существует множество команд, к которым относятся и сдвиги: Все сдвиги похожи друг на друга поведением средних битов: они просто сдвигаются влево или вправо на определённую величину. И различаются поведением крайних битов: одного, который уходит из слова, и второго, который должен появиться в слове.

Логический сдвиг

Логический сдвиг влево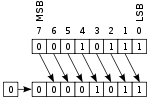

Логический сдвиг вправо

Сдвиг, при котором уходящий бит уходит, не влияя на оставшееся биты, а на место появившегося бита записывается бит 0.

Пример работы операции сдвига:

Пусть у нас есть число 10101010b (в двоичной системе).

Если сделать сдвиг влево на 1 бит, то получим число 01010100b

Если сделать сдвиг вправо на 1 бит, то получим число 01010101b

В большинстве процессоров уходящий бит сохраняется в флаге переноса. Эта функция широко используется при работе с многобайтовыми числами.

Арифметический сдвиг

Арифметический сдвиг влево

Арифметический сдвиг вправо

При этом сдвиге слово рассматривается не просто как группа битов, а как целое число в дополнительном коде. При сдвиге влево ведёт себя как логический сдвиг, при сдвиге вправо: уходящий бит уходит, не влияя на оставшееся биты, а на место появившегося бита устанавливается бит, соответствующий знаку.

Пример работы операции сдвига:

Пусть у нас есть число 11111010b=−6 (в двоичной системе).

Если сделать сдвиг влево на 1 бит, то получим число 11110100b=−12

Если сделать сдвиг вправо на 1 бит, то получим число 11111101b=−3

Легко заметить, что при арифметическом сдвиге сдвиг влево соответствует умножению на 2, а сдвиг вправо делению на 2 (в общем случае — на основание системы счисления). Исключение: −1 >>a 1 = −1 (в общем случае это относится к числам от −1 до −p+1, где p — основание системы счисления).

Схемотехническая реализация операций сдвига очень проста. Именно поэтому эти операции рекомендуют использовать для операций умножения и деления целых чисел на числа равные степени 2 (2, 4, 8, 16, 32, 64 и т. д.).

Циклический сдвиг

Циклический сдвиг влево

Циклический сдвиг вправо

При этом сдвиге уходящий бит появляется на месте появившегося.

Пример работы операции сдвига:

Пусть у нас есть число 11111010b (в двоичной системе).

Если сделать сдвиг влево на 1 бит, то получим число 11110101b

Если сделать сдвиг вправо на 1 бит, то получим число 01111101b

Циклический сдвиг через бит переноса

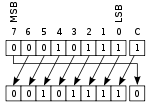Циклический сдвиг влево через бит переноса

Циклический сдвиг вправо через бит переноса

В архитектуру многих процессоров входит флаг переноса в следующий разряд (например, cf на n+1)-битным числом, состоящим из регистра и флага переноса.

Например, если у нас в регистре число 11111010b, флаг переноса равен 0:

После сдвига влево на 1 бит: в регистре 11110100b, флаг переноса равен 1

После сдвига вправо на 1 бит: в регистре 01111101b, флаг переноса равен 0

Операция циклического сдвига через бит переноса используется при работе с многобайтовыми числами. В частности, чтобы сдвинуть вправо на 1 бит длинное число, нужно очистить[1] cf (в случае деления числа со знаком нужно записать в cf старший бит старшего слова) и циклически сдвинуть на единицу через cf каждое слово, начиная с верхнего. Например, пусть у нас есть число 011000111100b, занимающее три 4-битных слова:

Было:              HI=0110, MED=0011, LO=1100, cf=0
После сдвига HI:   HI=0011, MED=0011, LO=1100, cf=0
После сдвига MED:  HI=0011, MED=0001, LO=1100, cf=1
После сдвига LO:   HI=0011, MED=0001, LO=1110, cf=0

Сдвиги через регистр флагов более чем на 1 бит практически не используются.

Примечания

1. ↑ Можно вместо очистки флага для первого обрабатываемого слова использовать арифметический\логический сдвиг, если он присваивает флагу cf значение вышедшего бита.

Источник

• Лекция: «Битовые операции»
• «Assembler&Win32. Курс молодого бойца.» Урок 11. «Биты, сдвиг логический, арифметический и циклический.»