- Композиция отображений
-
Компози́ция фу́нкций (суперпози́ция фу́нкций) в математике — это применение одной функции к результату другой.
Композиция функций F и G обычно обозначается
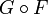 .
.Содержание
Определение
Пусть
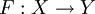 и
и 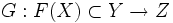 две функции. Тогда их композицией называется функция
две функции. Тогда их композицией называется функция 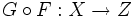 , определённая равенством:
, определённая равенством: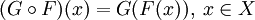 .
.
Связанные определения
- Термин «сложная функция» может быть применим к композиции двух функций, тем не менее он чаще употребляется в ситуации когда на вход функции нескольких переменных подаётся набор функций от одной или нескольких исходных переменных. Например функция G вида
- G(x,y) = F(u(x,y),v(x,y))
Свойства композиции
- Композиция ассоциативна:
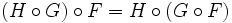 .
.
- Если F = idX — тождественное отображение на X, то есть
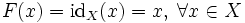 ,
,
- то
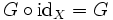 .
.
- Если G = idY — тождественное отображение на Y, то есть
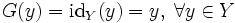 ,
,
- то
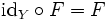 .
.
- Рассмотрим пространство всех биекций множества X на себя и обозначим его
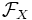 . То есть если
. То есть если 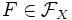 , то
, то 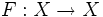 — биекция. Тогда композиция функций из
— биекция. Тогда композиция функций из 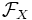 является бинарной операцией, а
является бинарной операцией, а 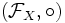 — группой. idX является нейтральным элементом этой группы. Обратным к элементу
— группой. idX является нейтральным элементом этой группы. Обратным к элементу 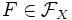 является
является 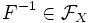 — обратная функция.
— обратная функция.
- Группа
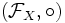 , вообще говоря, не коммутативна, то есть
, вообще говоря, не коммутативна, то есть 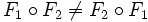 .
.
- Группа
Дополнительные свойства
- Композиция непрерывных функций непрерывна. Пусть
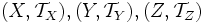 — топологические пространства. Пусть
— топологические пространства. Пусть 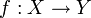 и
и 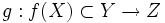 две функции,
две функции, 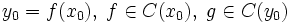 . Тогда
. Тогда 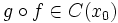 .
.
- Композиция дифференцируемых функций дифференцируема. Пусть
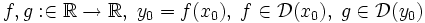 . Тогда
. Тогда 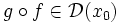 , и
, и
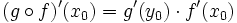 .
.
Wikimedia Foundation. 2010.
