Формула Бине-Коши

Формула Бине-Коши

Формула Бине—Коши — теорема об определителе произведения двух прямоугольных матриц, при условии, что оно является квадратной матрицей. Доказана в начале XIX века французскими математиками Бине и Коши.

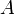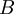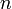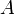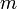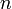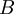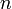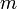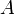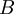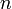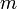Произведение двух прямоугольных матриц $\,A$ и $\,B$ дает квадратную матрицу порядка $\,n$, если $\,A$ имеет $\,m$ столбцов и $\,n$ строк, а матрица $\,B$ имеет $\,n$ столбцов и $\,m$ строк. Миноры матриц $\,A$ и $\,B$ одинакового порядка, равного наименьшему из чисел $\,n$ и $\,m$, называются соответствующими друг другу, если они стоят в столбцах (матрицы 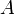$\,A$) и строках (матрицы 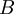$\,B$) с одинаковыми номерами.

Определитель матрицы 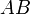$AB\,$ равен нулю, если 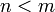$\,n<m$, и равен сумме попарных произведений соответствующих друг другу миноров порядка 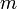$\,m$, если 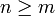$n \ge m$ (сумма берется по всем наборам столбцов матрицы 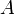$\,A$ и строк матрицы 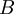$\,B$ с возрастающими номерами $i_1 < i_2 < \ldots < i_m$).

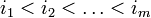• В случае 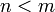$\,n<m$ формула 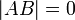$|AB|=0\,$ очевидна. Действительно, так как столбцы матрицы 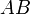$AB\,$ являются линейными комбинациями столбцов матрицы 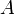$\,A$, то в случае, когда число столбцов матрицы 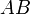$AB\,$ больше числа столбцов матрицы 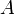$\,A$, матрица 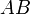$AB\,$, очевидно, является вырожденной (т.е. её определитель равен нулю).

• В случае 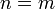$\,n=m$ формула Бине—Коши принимает хорошо известный вид: $\,|AB|=|A|\,|B|$.

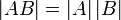• В случае 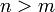$\,n>m$ доказательство формулы Бине—Коши более сложно.

Пример

Пусть

$A = \left(\begin{matrix} a_1 \! & a_2 & \! \cdots \! & \! a_n \! \\ b_1 \! & b_2 & \! \cdots \! & \! b_n \\ \end{matrix}\right), \quad B = \left(\begin{matrix} \! a_1 & b_1 \! \\ \! a_2 & b_2 \! \\ \! \vdots & \vdots \! \\ \! a_n & b_n \! \\ \end{matrix}\right).$

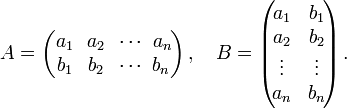
Тогда $A\,B = \left(\begin{matrix} a_1^2 \, + \, a_2^2 \, + \ \cdots \ + \, a_n^2 & {}\quad a_1b_1 + a_2b_2 + \cdots + a_nb_n \! \\ a_1b_1 + a_2b_2 + \cdots + a_n b_n & \ b_1^2 \, + \, b_2^2 \, + \ \cdots \ + \, b_n^2 \\ \end{matrix}\right),$

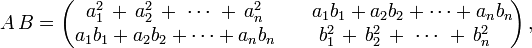
и соответствующие миноры имеют вид 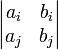$\left|\begin{matrix} a_i & b_i \\ a_j & b_j \\ \end{matrix}\right|$ при всех i < j, принимающих значения от 1 до n.

Формула Бине—Коши в этом случае дает равенство

$(a_1^2 + a_2^2 + \cdots + a_n^2)(b_1^2 + b_2^2 + \cdots + b_n^2) - (a_1b_1 + a_2b_2 + \cdots + a_nb_n)^2 = \sum_{i<j} (a_i b_j - a_j b_i)^2,$

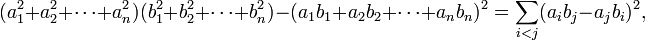
из которого (в случае, когда все a_i и b_i являются вещественными числами) вытекает неравенство Коши — Буняковского:

$(a_1^2 + a_2^2 + \cdots + a_n^2) (b_1^2 + b_2^2 + \cdots + b_n^2) \ge (a_1b_1 + a_2b_2 + \cdots + a_nb_n)^2.$

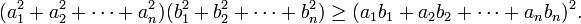
Литература

• Гантмахер Ф. Р. Теория матриц, — Наука, Москва, 1966.
• Фаддеев Д. К. Лекции по алгебре, — Наука, Москва, 1984.
• Шафаревич И. Р., Ремизов А. О. Линейная алгебра и геометрия, — Физматлит, Москва, 2009.