ТОПОЛОГИЧЕСКИЙ ФАЗОВЫЙ ПЕРЕХОД

ТОПОЛОГИЧЕСКИЙ ФАЗОВЫЙ ПЕРЕХОД

(переход Березинского - Костерлица - Таулесса, переход Костерлица- Таулесса) - фазовый переход в нек-рых вырожденных физ. системах между высоко- и низкотемпературной фазами, к-рые характеризуются отсутствием дальнего порядка, но различаются видом пространственной зависимости корреляц. ф-ций: в высокотемпературной фазе эта зависимость имеет вид экспоненциального спадания с расстоянием, а в низкотемпературной-степенного. Это означает, что ниже темп-ры T. ф. п. система "чувствует" локальное возмущение на больших расстояниях, что проявляется, напр., в расходимости восприимчивости планар-ного ферромагнетика, а также в существовании отличной от нуля сверхтекучей плотности в сверхтекучей жидкости и поперечной жёсткости в двумерных кристаллах (см. Двумерные решёточные модели).

T. ф. п. вообще характерен для физ. систем низкой пространственной размерности (d =1 или 2), для к-рых выполняется Мёрмина - Вагнера теорема (см. [1]) о разрушении дальнего порядка в таких системах тепловыми флуктуациями при 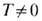(соответствующий параметр дальнего порядка является при этом двух- или многокомпонентным. n>=2). Примерами таких систем могут служить нек-рые системы, описываемые спи новым гамильтонианом, а также системы, обнаруживающие явления сверхтекучести, сверхпроводимости и т. п.

Схематическое изображение вихря ( а )и антивихря ( б) на примере планарного магнетика (стрелки - векторы спиновых магнитных моментов).

T. ф. п. теоретически описан в работах [2, 3].

T. ф. п. обычно обусловлен топологич. возбуждениями- т. н. в и х р я м и, к-рые в кристаллах с d=2 совпадают с винтовыми дислокациями. Каждый изображённый на рис. вихрь (или, соответственно, антивихрь) характеризуется топологическим зарядом q= +1(соответственно, q= -1), к-рый выражается математически в виде 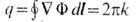(k - целое число) в случае планарного ХY -магнетика и сверхтекучей жидкости (интегрирование проводится по замкнутому контуру, окружающему сердцевину топологической особенности). Для этих физ. систем Ф имеет соответственно смысл угла поворота вектора спина S = S(cos Ф,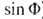) или потенциала поля сверхтекучей скорости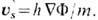

Вихри взаимодействуют между собой подобно двумерному кулоновскому газу - по логарифмич. закону. Энергия взаимодействия двух топологич зарядов q₁ и q₂, расположенных в точках r₁ и r₂, выражается в виде 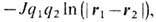где величина J порядка обменной энергии в магнетике или порядка характерных значений упругих модулей в кристалле. При низких темп-pax пары вихрь - антивихрь образуют своего рода "молекулярный" газ; при достижении критич. темп-ры T. ф. п. часть "молекул" диссоциирует и свободные вихри и антивихри образуют нейтральную (в смысле топологич. заряда) "плазму". На основе этой аналогии в сочетании с ренормгрупповым подходом Дж. M. Костерлиц и Д. Д. Таулесс [3] определили темп-ру T. ф. п. и установили универсальность критич. поведения корреляц. ф-ций. T. ф. п. в двумерном кристалле, атомы к-рого образуют треугольную решётку (см. Вигнеровский кристалл), имеет характер своеобразного "плавления", при к-ром в низкотемпературной фазе существует позиционная жёсткость, исчезающая при нек-рой темп-ре T₁; выше этой темп-ры продолжает существовать ориентационная жёсткость, к-рая также разрушается при темп-ре Т₂>Т₁.

Эксперим. изучение T. ф. п. затруднено сложностью приготовления истинно низкоразмерных физ. систем; как правило, различные, достаточно малые взаимодействия придают системе квазидвумерный характер и маскируют T. ф. п. Влияние подобных факторов на T. ф. п. и др. физ. свойства XY -подобных систем изучены в работах [4], [5].

Лит.:1)Mermin N., Wagner H., Absence of ferromagnetism or antiferromagnetism in one- or two-dimensional isotropic Heisenberg models, "Phys. Rev. Lett.", 1966, v. 17, p. 1133; 2) Березин-ский В. Л., Разрушение дальнего порядка в одномерных и двумерных системах с непрерывной группой симметрии, "ЖЭТФ", 1970, т. 59, с. 907; 1971, т. 61, с. 1144; 3) Kosterlitz J. M., Thou-less D. J., Ordering metastability and phase transitions in 2 dimensional systems, "J. Phys. C.", 1973, v. 6, p. 1181. 4) Покровский В. Л., Уймин Г. В., Магнитные свойства плоских и слоистых систем, "ЖЭТФ", 1973, т. 65, с. 1691; 5) Jose J. V. [а. о.], Renormalization, vortices and symmetry-breaking perturbations in the 2-dimensional planar model, "Phys. Rev.", 1976, v. В16, p. 1217.

Г. В. Уймин.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.