ТОПОЛОГИЯ ВСЕЛЕННОЙ

ТОПОЛОГИЯ ВСЕЛЕННОЙ

-топологич. свойства пространственно-временного многообразия, к-рым описывается Вселенная согласно общей теории относительности и в к-рое вложены негравитац. физ. поля и частицы. Эти свойства не изменяются при любых непрерывных преобразованиях пространства-времени (см. Топология). К наиб. общим свойствам T. В. относятся её размерность и связность. Наблюдаемая размерность Вселенной равна 4 (одна временная и три пространственные координаты), а наблюдаемая связность тривиальна, т. е. видимая часть Вселенной является односвязным пространственно-временным многообразием, в ней нет "дыр" (существование чёрных дыр, возникших в результате коллапса звёзд, а также первичных чёрных дыр не ведёт к возникновению неодносвязности в 4-мерном смысле). Это не исключает возможности того, что в очень малых масштабах [порядка план-ковской длины 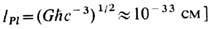Вселенная может иметь большую размерность (как это предполагается в теориях типа Калуцы - Клейна или в суперструн теориях; см. Калуцы-Клейна теория )или более сложную связность (т. н. пространственно-временная пена в квантовой гравитации). Вселенная также может быть многосвязной в масштабах порядка совр. космология, горизонта 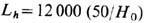Мпк [при законе расширения Вселенной в настоящее время 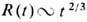, где R(t)- масштабный фактор, a H₀ -Хаббла постоянная в км·с ^-1·Мпк ^-1] и более; в меньших масштабах большинство возможных нетривиальных топологий исключается наблюдательными данными, в частности структурой угл. флуктуации темп-ры микроволнового фонового излучения (И. Ю. Соколов, 1993; А. А. Старобинский, 1993; Дж. Силк, 1993). Наконец, мыслимо также существование других вселенных, полностью отъединённых от нашей с точки зрения классич. гравитации, но связанных в одно целое квантово-гравитац. эффектами. Однако пока не найдено возможности проверить эту гипотезу на опыте. Топологич. свойствами нашей Вселенной является также её ориентируемость (приводящая к важным ограничениям на возможные симметрии взаимодействия элементарных частиц) и отсутствие замкнутых времениподобных мировых линий ("машин времени").

Говоря о T. В., следует отличать 4-мерную топологию пространственно-временного многообразия, к-рым она описывается, от её пространственной топологии, т. е. топологии 3-мерной гиперповерхности пост. времени во Вселенной. В качестве последней обычно выбирают гиперповерхность пост. плотности вещества r (или плотности энергии материи), поскольку в однородных космологич. моделях r является однозначной ф-цией времени t в синхронной системе отсчёта. Пространственная T. В. может быть нетривиальной (т. е. не R³ )даже при тривиальной (R⁴)4-мерной топологии, если выбранная гиперповерхность не является гиперповерхностью Коши, т. е. не пересекает всего пространства-времени. Такое поведение гиперповерхности r = const не является исключительным и естественно возникает, напр., в теории раздувающейся Вселенной в послеинфляц. период.

В однородной и изотропной Вселенной, описываемой Фридмана-Робертсона-Уокера метрикой,T. В. однозначно связана со знаком следа пространственной кривизны тензора Р ис . соотношением между полной плотностью вещества и критич. плотностью 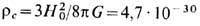(H₀/50)² г/см ³ , где G- ньютоновская гравитационная постоянная, а именно: если r>r_c, то P>0, Вселенная пространственно замкнута (имеет пространственную топологию 3-мерной сферы) и сколлапсирует как целое в будущем (при отсутствии положит. космологич. постоянной), в обратном случае, r<=r_c, Вселенная имеет тривиальную пространственную топологию R³, бесконечный объём сечения t =const и будет бесконечно расширяться в будущем (см. Космология). В прошлом это вызывало неоднократную философскую критику пространственно замкнутой Вселенной. В настоящее время ясно, что такая связь между локальными характеристиками Вселенной и её глобальной топологией возникла только в результате необоснованного предположения об абс. однородности и изотропии Вселенной. В слабо неоднородной и анизотропной Вселенной однозначной связи между величиной r/r _с, к-рая определяет локальный знак P, и T. В. нет. Напр., теория раздувающейся Вселенной предсказывает, что в масштабах, много больших совр. космологич. горизонта L_h, гиперповерхность r=const может иметь нетривиальную топологию, хотя всюду локально 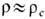Этот эффект, однако, обязательно связан с возникновением большой неоднородности в таких же (и даже меньших) масштабах. Обратно, из наблюдаемого факта приближённой однородности и изотропии Вселенной в масштабе порядка L_h следует, что пространственная T. В. должна быть тривиальной в том же масштабе. В этом смысле теория раздувающейся Вселенной объясняет наблюдательный факт отсутствия нетривиальной пространственной T. В.

Лит.: Зельдович Я. Б., Новиков И. Д., Строение и эволюция Вселенной, M., 1975; Хокинг С., Эллис Дж., Крупномасштабная структура пространства-времени, пер. с англ., M., 1977; Линде А. Д., Физика элементарных частиц и инфляционная космология, M., 1990. А. А. Старобинский.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.