- СФЕРИЧЕСКИЕ ФУНКЦИИ
- СФЕРИЧЕСКИЕ ФУНКЦИИ
-
(сферические гармоники) - спец. функции, возникающие, напр., при отыскании ограниченных решений ур-ния Лапласа Du = 0 в сферич. координатах (r, q, j) методом разделения переменных. Введены в кон. 18 в. А. Лежандром и П. Лапласом. Полагая и = и(r,q, j) = R(r)Y(q,j), после разделения переменных для Y(q, j) получаем ур-ние
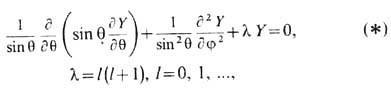
частные решения к-рого - С. ф.- имеют вид звёздочка означает комплексное сопряжение. Ф-ция Qlт (х)(x = cosq) может быть выражена через полиномы Якоби Pl(a,b)(x), присоединённые ф-ции Лежандра Р ml (х )и полиномы Лежандра Pl(X )(см. Ортогональные полиномы):
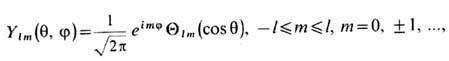
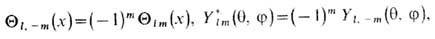
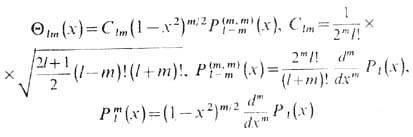
[в нек-рых работах по квантовой механике в коэф. С lт вводят дополнит. множитель (-1)mil]. Общий вид решения ур-ния (*)

( С m - постоянные).
С. ф. образуют полную ортонормированную систему на сфере единичного радиуса (d - дельта-функция,dnn' - Кронекера символ). Эта система играет ту же роль в разложении ф-ций на сфере, что и тригонометрич. ф-ции на окружности. Для ф-ций Ylm(q, j) построены конечно-разностные ортогональные аналоги на дискретном множестве точек сферы.
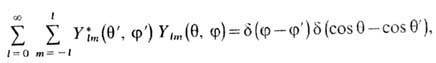
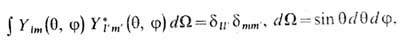
Рекуррентное соотношение и ф-лы дифференцирования для С. ф. имеют вид
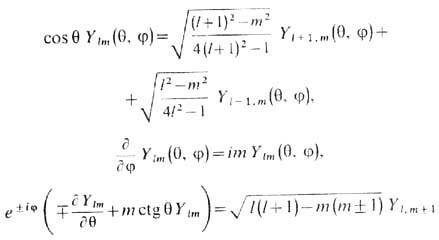
[при т=b(l+1) следует полагать Ylm(q, j) = 0].
Теорема сложения для С. ф. выражает полином Лежандра Pl(cosw) [w - угол между векторами r1 и r2, направления к-рых характеризуются углами q1, j1 и q2, j2:
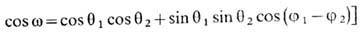
через произведения С. ф.:
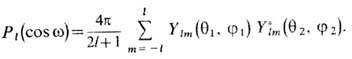
С помощью этой теоремы можно записать разложение потенциала (в точке r1) единичного заряда (расположенного в точке r2 )в виде
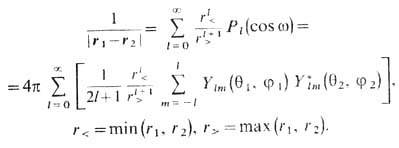
При вращении системы координат, определяемом углами Эйлера a, b, g, С. ф. преобразуются след, образом:
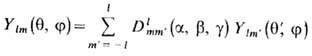
(q', j'-углы q, j в новой системе координат). Коэф. Dlmm'(a, b, g) наз. обобщёнными С. ф., или Вигнера функциями. Они связаны со С. ф. соотношениями

Лит.: Гобсон Е. В., Теория сферических и эллипсоидальных функций, пер. с англ., М., 1952; Бейтмен Г., Эрдейи А., Высшие трансцендентные функции, пер. с англ., 2 изд., т. 2, М., 1974; Никифоров А. Ф., Уваров В. Б., Специальные функции математической физики, 2 изд., М., 1984: Справочник по специальным функциям, пер. с англ., М., 1979. А. Ф. Никифоров.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
