СФЕРИЧЕСКИЕ ФУНКЦИИ

шаровые функции, присоединенные функции Лежандра 1-го и 2-го рода, - два линейно независимых решения и дифференциального уравнения

где 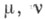- комплексные постоянные, к-рое возникает при решении нек-рых классов дифференциальных уравнений с частными производными методом разделения переменных. Точки являются в общем случае точками ветвления решений. С. ф. являются частными случаями гипергеометрич. функции: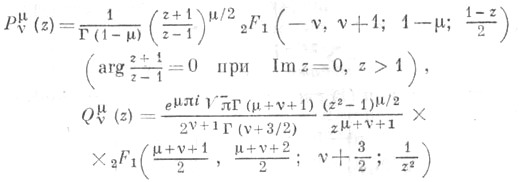

(arg z=0 при Im z=0, z > 0; arg(z²-1)=0 при Im z=0, z > 1).
С. ф. и определены и однозначны соответственно в областях |1-z|<2 и |z| >1 комплексной плоскости, разрезанной вдоль действительной оси от до +1.
Если Im z=0, z=x, -1<x<1, то обычно в качестве решений рассматриваются функции

где f(x+i0) (f( х-i0)).- значения функции f(z) на верхней (нижней) границе разреза.
При v=n=0, 1, 2, ... - многочлены Лежандра. О зональных С. ф. см. ст. Сферическая гармоника.

Лит.:[1] Бейтмен Г., Эрдейи А., Высшие трансцендентные функции, пер. с англ., 2 изд., т. 2, М., 1974; [2] Справочник по специальным функциям с формулами, графиками и математич. таблицами, пер. с англ., М., 1979; [3] Уиттекер Э. Т., Ватсон Д ж. Н., Курс современного анализа, пер. с англ., 2 изд., ч. 2, М., 1963; [4] Кратцер А., Франц В., Трансцендентные функции, пер. с нем., М., 1963; [5] Гобсон Е. В., Теория сферических и эллипсоидальных функций, пер. с англ., М., 1952.
Ю. А. Брычков, А. П. Прудников.