- СРЕДНЕГО ПОЛЯ ПРИБЛИЖЕНИЕ
- СРЕДНЕГО ПОЛЯ ПРИБЛИЖЕНИЕ
-
(молекулярное поле, эффективноеполе) - один из методов приближённого описания эффектов многочастичныхвзаимодействий в задачах многих тел в квантовой механике и квантовой статистике. <С, п. п. применяется в тех случаях, когда точное решение задачи отсутствует, <а учёт конечного числа членов ряда возмущений теории недостаточен(напр., если константа взаимодействия не мала или ряды теории возмущенийобладают плохой сходимостью). С. п. п. состоит обычно в эфф. «линеаризации»гамильтониана взаимодействия мн, частиц, т. е. в замене его соответственноподобранным гамильтонианом одночастичного взаимодействия с нек-рым эфф.«полем», параметры к-рого следует определить самосогласованным образом. <Физически такая замена соответствует переходу от «близкодействия» к «дальнодействию»,т. е. к постоянному (не зависящему от расстояния) многочастичному взаимодействиюс формально бесконечным радиусом, а также пренебрежению корреляц. эффектами. <Несмотря на такое упрощение решения задачи мн. тел С. п. п. в большинствеслучаев качественно правильно описывает физ. свойства очень широкого классареальных систем мн. тел, в первую очередь сложных атомов, молекул, жидкостейи твёрдых тел (см. Самосогласованное поле, Хартри - Фока метод).
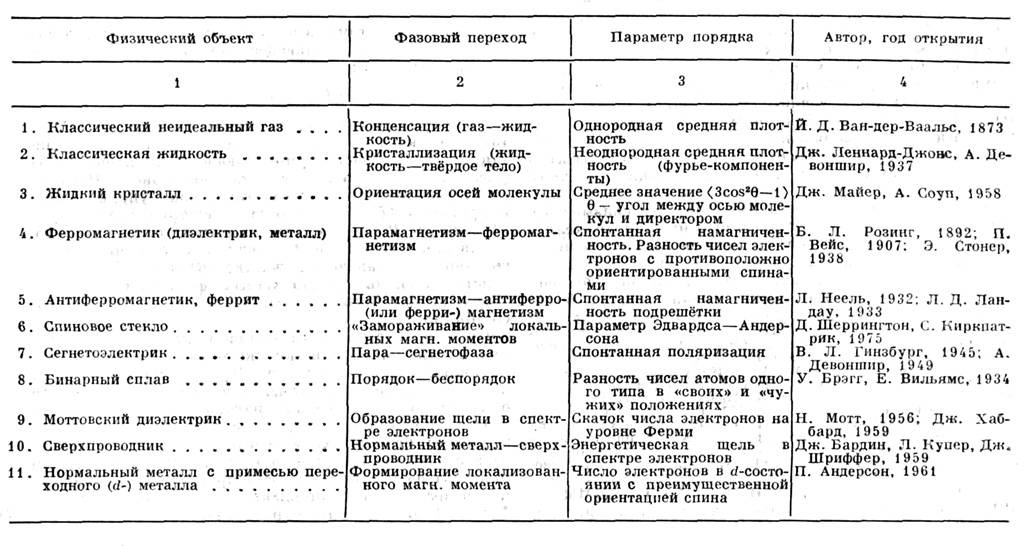
Особенно важное значение С. п. п. имеет для решения задач физики конденсиров. <состояния, прежде всего для описания разл. подсистем в твёрдых телах (столбец1 в табл.), испытывающих разнообразные фазовые переходы (структурные, <ориентационные, магнитные, сверхпроводящие и т. п.- столбец 2 в табл.).В подобных системах среднее поле (СП) принимается обычно пропорциональным параметру порядка (столбец 3 в табл.), т. е. ср. значению оператораупорядочения (оператор, описывающий динамическую переменную, испытывающуюупорядочение). Физически это означает пренебрежение квантовыми флуктуациямиэтого оператора и построенными на них высшими корреляционными функциями. При этом СП оказывается зависящим от внеш. полей, темп-ры и др. интенсивныхтермодинамич. параметров (для структурно неупорядоченных систем СП можетбыть неоднородным, т. е. зависеть от координат). С. п. п. позволяет вычислить статистическую сумму и все термодинамич. ф-ции системы. Дальнейшаяпроцедура самосогласования приводит обычно к достаточно простому ур-нию(в большинстве случаев - трансцендентному, иногда, как в случае сверхпроводника,-интегральному) для параметра порядка. Это ур-ние имеет нетривиальные (отличныеот нуля) решения лишь ниже определ. темп-ры Т к, называемой критической точкой или точкой фазового перехода 1-го или 2-го рода. <При этом значение энергии взаимодействия системы со СП в осн. состояниипри Т = 0 составляет величину порядка kTk.
Физ. смысл СП столь же разнообразен, сколь разнообразны виды системи параметров порядка; как правило, СП определяется произведением параметрапорядка на ср. энергию взаимодействия частиц системы. Так, в магнитоупорядоченныхвеществах (в т. ч. спиновых стёклах )и сегнетоэлектриках это- обменное взаимодействие, в сверхпроводниках - электрон-фо-нонное взаимодействие, <в переходах металл - диэлектрик - внутриатомное кулоновское отталкиваниемежду электронами, в классич. газах и жидкостях - межмолекулярное притяжениеи т. п. До возникновения микроскопич. описания С. п. п. вводилось чистофеноменологически и лишь затем получало обоснование и истолкование черезмикроскопич. параметры; как видно из столбца 4 таблицы, С. п. п. фактическиприменяется уже более ста лет, т. е. задолго до возникновения квантовойтеории.
Исторически первое целенаправленное введение СП (тогда - внутреннего, <или молекулярного, поля) считается принадлежащим Б. Л. Розингу (1892) иП. Вейсу (P. Weiss, 1907), применившим его в теории ферромагнетизма дляобъяснения существования спонтанной намагниченности. Однако ещё задолгодо этого И. Д. Ван-дер-Ваальс (J. D. Van der Waals, 1873) фактически использовалпонятие СП для учёта межмолекулярного взаимодействия при выводе ур-ниясостояния классич. неидеального газа.
В дальнейшем (30-е гг. 20 в.) С. п. п. плодотворно применялось рядомавторов к широкому классу объектов (антиферромагнетики, ферриты, бинарныесплавы и т. п.), а позднее (40-50-е гг.) - к сегнетоэлектрикам, сверхпроводниками др. С. п. п. успешно используется также в теории неупорядоченных систем (аморфные твёрдые тела, спиновые стёкла и т. п.). Практически все этисистемы могут быть описаны с помощью эффективного спинового гамильтониана. При этом оператором упорядочения является одна из компонент Sa оператора спина (квазиспина) S. В магнитоупорядоченных веществахтаким оператором будет продольная (Изинга модель )или поперечная(ХУ-модель; см. Двумерные решёточные модели )компонента оператораспина. В сверхпроводниках оператором упорядочения является поперечная компонентаоператора квазиспина (совпадающая с оператором рождения куперовской пары),в ферромагн. металле - продольная компонента оператора квазиспина (разностьоператоров числа электронов с противоположными спинами). Процедура введенияСП состоит в замене одного из операторов
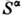 егоср. значением
егоср. значением 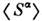 ,что позволяет линеаризовать гамильтониан и получить точное решение в рамкахданной модели.
,что позволяет линеаризовать гамильтониан и получить точное решение в рамкахданной модели.С. п. п. фактически эквивалентно применению вариационного принципа Н. <Н. Боголюбова для свободной энергии (напр., применительно к магн. диэлектрикам),а также методу Л. Д. Ландау (Ландау теория )разложения свободнойэнергии по степеням параметра порядка вблизи критич. точки и гауссовомуприближению в методе континуального интегрирования для статистич. суммы. <Ввиду своей физ. наглядности и матем. простоты С. п. п. является, как правило, <необходимым первоначальным этапом решения задачи мн. тел практически длялюбой системы, особенно при наличии в ней дополнит. усложнений - сложнойструктуры кристаллич. или магн. элементарной ячейки, нарушения регулярнойструктуры кристалла, т. е. наличия примесей, вакансий и др. дефектов (см.,напр., Магнитный фазовый переход). Однако в рамках С. п. п. невозможноописать динамич. свойства систем, прежде всего спектр элементарных возбуждений, <резонансные свойства и т. п.
Применимость С. п. п. имеет определ. ограничения. Прежде всего оно теряетпригодность в тех случаях, когда флуктуации параметра порядка играют существ. <роль, напр. в непосредств. окрестности точек фазовых переходов, где С. <п. п. даёт завышенные значения самих этих точек, а также не согласующиесяс экспериментом значения критических показателей. С. п. п. не «чувствует»тонких различий между нек-рыми системами (напр., ферромагнетиками Изингаи Гейзенберга) и даёт значения критич. показателей, не зависящие ни отразмерности решётки d, ни от размерности параметра порядка п. К системам с низкой размерностью (d -1,2), для к-рых имеющиесяточные решения модельных задач или общие теоремы квантовой статистич. механикиуказывают на отсутствие фазовых переходов, С. п. п. вообще неприменимо.
Одним из обобщений С. п. п. (используемых, в частности, для магн. исегнетоэлектрич. систем) является разложение свободной энергии и корреляц. <ф-ций по обратным степеням радиуса обменного воздействия. Широко применяетсятакже метод ренормализационной группы и e-разложения, приводящийк появлению «траекторий» на плоскости ( п, d )для критич. показателей, <значения к-рых близки к экспериментально наблюдаемым.
Другим важнейшим обобщением С. п. п. является т. н. приближение случайныхфаз (ПСФ), к-рое представляет собой развитие идеи усреднения соответствующихоператоров упорядочения. При этом усреднение операторов осуществляетсяне в гамильтониане, а при записи квантового уравнения движения. наиб. завершениеэта идея получила в методе ф-ций Грина. В квантовой теории магнетизма ПСФносит название приближения Тябликова, в теории сверхпроводимости - Бардина- Купера - Шриффера модели, в теории неупорядоченных систем - приближениякогерентного потенциала. ПСФ соответствует учёту влияния на каждое одночастичноесостояние не только ср. статич. поля, как в С. п. п., но и переменных (осциллирующих)добавок к нему, возникающих благодаря частичному учёту корреляции междудвижениями различных (квази) частиц.
С. п. п. соответствует учёту только дальнего порядка, однако существуетряд способов его улучшения с целью учёта также эффектов корреляции, проявляющихсяв наличии ближнего порядка. Среди них наиб. известны т. н. кластерные приближе-ни я. При этом оператор упорядочения задаётся не для узла решётки, а длякластера, включающего, напр., первую координац. сферу.
Лит.: Ландау Л. Д., Л и ф ш и ц Е. М., Статистическая физика, <ч. 1, 3 изд., М., 1976, гл. 6, 7, 13, 14; Л а н д а у Л. Д., ПитаевскийЛ. П., Статистическая физика, ч. 2, М., 1978; Т а у л е с Д., Квантоваямеханика систем многих частиц, пер. с англ., 2 изд., М., 1975; ТябликовС. В., Методы квантовой теории магнетизма, 2 изд., М., 1975; Б р а у тР., Фазовые переходы, пер. с англ., М., 1967; Смарт Д ж., Эффективное полев теории магнетизма, пер. с англ., М., 1968; Стенли Г., Фазовые переходыи критические явления, пер. с англ., М., 1973; И з ю м о п Ю. <А., К а с с а н - О г л ы Ф. А., Скрябин Ю. Н., Полевые методы в теорииферромагнетизма, М., 1974; Жирифалько Л., Статистическая физика твердоготела, пер. с англ., М., 1975; М а Ш., Современная теория критических явлений, <пер. с англ., М., 1980; Займан Дж., Модели беспорядка, пер. с англ., М.,1982. А. В. Ведяев, Ю. Г. Рудой.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
