СПЕКТРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ

СПЕКТРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ

матричных элементов матрицы рассеянияS или Грина функций в квантовой теории поля - интегральные представлениятипа Коши интеграла. С. п. играют большую роль в аксломатрич. подходек квантовой теории поля (см. Аксиоматическая квантовая теория поля), врамках к-рого построение матрицы рассеяния осуществляется без конкретныхпредположений о взаимодействии, присущих гамильтонову формализму. Особенноважны С. п., к-рые удаётся получить на основе только самых общих положенийквантовой теории поля, таких, как требования микропричинности, унитарности(см. Унитарности условие), релятивистской инвариантности и предположенияо спектре масс. Так, напр., для ф-ции Грина G(x - у )из ур-ния скалярногополя 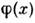массы т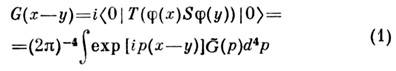

( Т - символ хронологич. упорядочения, р -4-импульс поля)на этой основе установлено важное С. п. Лемана - Келлена (Н. Lehmann, G.Kallen):

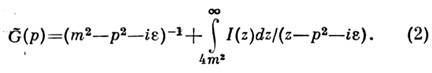
Здесь I(z) - неотрицат. ф-ция, описывающая распределение массвозможных состояний поля,- спектральная плотность масс, к-рая выражаетсячерез матричные элементы S-матрицы.

В общем случае вся информация о взаимодействии частиц содержится в матричныхэлементах S-матрицы, относящихся к переходу из состояния i невзаимодействующихначальных частиц в состояние f невзаимодействующих конечных частиц с 4-импульсамир ₁, ...,p_i, и 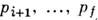.Приняв во внимание закон сохранения 4-импульса (и др. следствия релятивистскойинвариантности), такой матричный элемент можно записать в виде: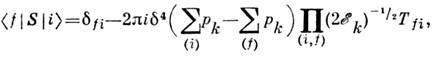

где амплитуда 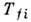перехода 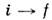- скалярная ф-ция 4-импульсов р, и поляризаций начальных и конечныхчастиц. Зависимость Т _fi от 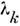поляризацийможно полностью выделить, представив Т'_fi каксумму членов вида: , причём 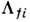- определённые матричные 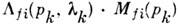элементы лоренц-инвариантных комбинаций, составленных из спиновых операторов. <С. п. строятся для скалярных ф-ций М _fi, называемых инвариантнымиамплитудами перехода 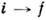.Зависимость 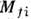от своих аргументов носит динамич. характер, и её существенные черты отражаютсяв аналитич. свойствах 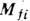.В частном случае, когда и в начальном, и в конечном состоянии имеется поодной частице,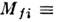

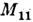связанас ф-цией Грина в (2) соотношениями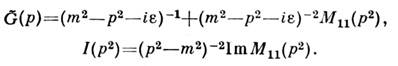

Ряд существенных сведений об аналитич. структуре М _fi можетбыть получен из общих положений квантовой теории поля, не зависящих отконкретной модели взаимодействия.

Прежде всего, использование микропричинности и нек-рых предположенийо свойствах спектра масс приводит к утверждению, что всякая инвариантнаяамплитуда является нек-рым граничным значением аналитич. ф-ции, зависящейтолько от лоренц-инвариантных комбинаций 4-импульсов р _k. Этограничное значение получается, когда квадрат полной энергии

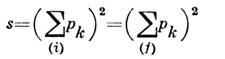
стремится к действит. оси сверху из области аналитичности, где он комплексени имеет положительную мнимую часть: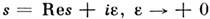. Инвариантные амплитуды обладают, кроме того, свойством перекрёстной симметрии. <Оно состоит в том, что амплитуды разл. каналов процесса взаимодействия(i + f) частиц, т. е. амплитуды, описывающие переходы с разл. распределениемданных (i + f) частиц на начальные и конечные, являются различными граничнымизначениями одной общей аналитич. ф-ции F. Амплитуда 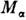каждого канала 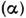получается из F, когда один из аргументов F - квадрат полнойэнергии в данном канале,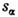устремлён к действит. оси сверху, а остальные аргументы принимают значенияв физ. области канала.

Условие унитарности S-матрицы позволяет установить, где ImF заведомоотлична от нуля. В каждом канале 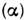инвариантная амплитуда 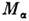как ф-ция 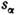имеет полюсы, соответствующие возможным одночастичным состояниям, и («физический»)разрез, соответствующий многочастичным состояниям в этом канале. Характеристикиэтих особенностей - вычеты в полюсах и скачки на физ. разрезах - могутбыть определены через матричные элементы S-матрицы с помощью той же унитарности. <Напр., т. н. абсорбционная часть амплитуды (т. е. скачок амплитуды на физ. <разрезе) равна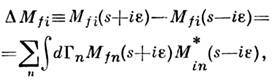

где в правой части проводится суммирование по всем возможным промежуточнымсостояниям ( п )и интегрирование но фазовому объёму в пространствеимпульсов каждого состояния (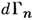- элемент фазового объёма). Если иных особенностей, кроме требуемых унитарностью, <у M_fi нет, интеграл Коши в комплексной плоскости 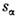представляет собой С. п. для 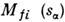Такая простая структура особенностей и составляет отличие С. п. от болееобщих дисперсионных соотношений. Как показывают результаты исследованийамплитуды переходов с 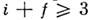, в частности примеры из теории возмущений, дисперсионные соотношения дляамплитуд этих переходов могут иметь т. н. аномальные разрезы, скачки нак-рых не определяются по условию унитарности. Так, для амплитуды упругогорассеяния M₂₂ на основе общих положений теории удалось доказатьлишь С. п. по квадрату полной энергии s при существенных ограниченияхна остальные аргументы М ₂₂, квадраты масс частиц и инвариантнуюпередачу импульса t. Однако ввиду их ясного физ. смысла С. Манделстам(S. Mandelstam) предложил принять без доказательства двойные С. п. по sи t для М ₂₂ хотя бы как основу простой теоретич. <модели процесса взаимодействия. Если для описания перехода частиц 1, 2в частицы 3,4 ввести инвариантные переменные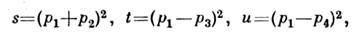

причём s, t, и связаны соотношением

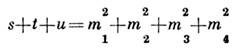
и являются квадратами полной энергии в каналах, где в качестве начальныхвыступают соответственно частицы 1 и 2, 1 и 3, 1 и 4, то т. н. двойноеС, п. Манделстама приобретает вид:

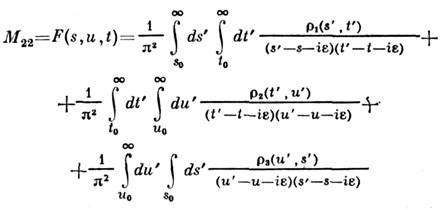
Интегрирование здесь ведётся от физ. порогов - квадрата суммы масс низшегопромежуточного состояния в соответствующих каналах. Такое С. п. обнаруживаетперекрёстную симметрию в самом виде записи. Для описания амплитуд всехтрёх каналов применяется одна ф-ция F(s, t, и), в частности однии те же определяющие её спектральные плотности 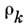.Переход, напр., от амплитуды s-канала к амплитуде t-канала осуществляетсязаменой s на г, a t на s. Это соответствует тому, что частица 2 замененана античастицу 3, а частица 3 на античастицу 2 в самом процессе. С. п. <Манделстама послужило основой мн. исследований процессов сильных взаимодействий.

Лит.: Новый метод в теории сильных взаимодействий. Сб. статей, <пер. с англ., под ред. А. М. Бродского, М., 1960; Боголюбов Н. Н., МедведевБ. В., Поливанов М. К., Вопросы теории дисперсионных соотношений, М., 1958;Бартон Г., Дисперсионные методы в теории поля, пер. с англ., М., 1968. В. <П. Павлов.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.