- ТОПОЛОГИЧЕСКИЙ СОЛИТОН
- ТОПОЛОГИЧЕСКИЙ СОЛИТОН
-
-солитон с нетривиальной топологич. характеристикой (типа степени отображения, инварианта Хопфа и т. <д.) - топологическим зарядом. В расширенном смысле (опуская присущее "истинным" солитонам свойство сохранения формы после столкновений) термин "Т.c." принято использовать как для обозначения топологически нетривиальных решений с конечными динамич. характеристиками в теории поля (кинков, монополей, инстантонов, скирмионов и т. д.), так и для модельного описания устойчивых неоднородных состояний (локализованных структур) в конденсированных средах: вихрей, дислокаций, дисклинаций, доменных стенок, точечных дефектов и т. п. ([1], [2]).
Простейшие (1 + 1)-мерные (пространственная координа-та+время) Т. <е. - кинки [от англ. kink - изгиб, петля, узел; термин предложен Д. Финкельштейном (D. Finkel-stein) в 1966 ] описываются решениями вида
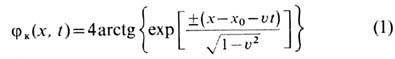
синус-Гордона уравнения (здесь и далее
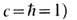
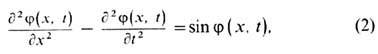
где j(x, t) - вещественная скалярная ф-ция, знак " + " в (1) соответствует к и н к у (знак "-" - а н т и к и н к у), находящемуся в момент времени t= 0 в точке x0 и движущемуся со скоростью uв направлении +х (соответственно - х для антикинка). Решения (1) удовлетворяют граничным условиям
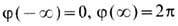 (рис. 1) и характеризуются топологич. зарядом
(рис. 1) и характеризуются топологич. зарядом
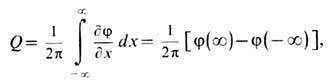
равным +1 соответственно для кинка и антикинка. Энергия кинка (антикинка)
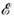 ограничена снизу величиной топологич. заряда
ограничена снизу величиной топологич. заряда 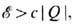 где с - константа, что обеспечивает его устойчивость в отношении распада на состояния с меньшей энергией (см. Устойчивость солитонов).
где с - константа, что обеспечивает его устойчивость в отношении распада на состояния с меньшей энергией (см. Устойчивость солитонов).
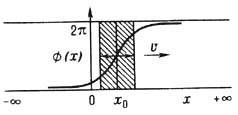
Рис. 1. Кинк уравнения синус Гордона, локализованный в точке х = х0, движущийся со скоростью uвнаправлении +х. Заштрихована область изгиба функции j, где сосредоточена основная часть энергии кинка.
Для наглядной иллюстрации кинка синус-Гордона ур-ния рассмотрим упругую полоску, уложенную вдоль оси x и характеризуемую в каждой точке оси углом закручивания (отклонения от равновесного положения края полоски) j(x) (рис. 2, а). Ф-цию j(x) можно задать непрерывным образом в случае полоски конечной длины 0<=x<=l, если наложить периодические граничные условия
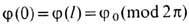 , т. е. отождествить концы полоски с точностью до 2p-кратного поворота. В результате получаем замкнутую полоску. Если до отождествления концов полоски повернуть один из них на угол 2p относительно оси х (к примеру по часовой стрелке), то после замыкания полоска будет содержать "скрутку" - кинк, к-рый не может быть устранён без разрыва полоски, т. е. будет сохраняться на протяжении всей последующей эволюции полоски (рис. 2, б). Для создания в полоске 2-кинкового состояния следует повернуть один из её концов (до отождествления) на угол 4p (рис. 2, в) и т. <д. Антикинк будет соответствовать закручиванию на 2p против часовой стрелки; понятно, что он будет "аннигилировать" с кин-ком, если их создать на одной и той же полоске.
, т. е. отождествить концы полоски с точностью до 2p-кратного поворота. В результате получаем замкнутую полоску. Если до отождествления концов полоски повернуть один из них на угол 2p относительно оси х (к примеру по часовой стрелке), то после замыкания полоска будет содержать "скрутку" - кинк, к-рый не может быть устранён без разрыва полоски, т. е. будет сохраняться на протяжении всей последующей эволюции полоски (рис. 2, б). Для создания в полоске 2-кинкового состояния следует повернуть один из её концов (до отождествления) на угол 4p (рис. 2, в) и т. <д. Антикинк будет соответствовать закручиванию на 2p против часовой стрелки; понятно, что он будет "аннигилировать" с кин-ком, если их создать на одной и той же полоске.
Синус-Гордона ур-ние (2), в частности, применяется для описания распространения дислокаций в кристаллах, движения Блоха стенок в магнитоупорядоченных средах и доменных стенок в сегнетоэлектриках, распространения квантов магн. потока (флаксонов) в длинных джозефсонов-ских контактах (см. Джозефсона эффект )и т. д.
Др. примером (1 + 1)-мерных Т. <е. являются кинки т. <н. j4 -модели с ур-нием

где параметры l, m2>=0 Модель простейшим образом иллюстрирует явление спонтанного нарушения симметрии. Действительно, ур-ние (3) допускает два решения-константы
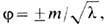 отвечающих нулевому уровню энергии
отвечающих нулевому уровню энергии  к-рые переводятся друг в друга (неинвариантны) при преобразованиях отражения
к-рые переводятся друг в друга (неинвариантны) при преобразованиях отражения 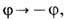 в то время как ур-ние (3) и соответствующий лагранжиан инвариантны при таких отражениях. В квантовом варианте указанным постоянным решениям отвечают два вырожденных вакуумных состояния
в то время как ур-ние (3) и соответствующий лагранжиан инвариантны при таких отражениях. В квантовом варианте указанным постоянным решениям отвечают два вырожденных вакуумных состояния 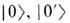 (см. Вырождение вакуума). Выбор любого из этих вакуумов приводит к теории со спонтанно нарушенной отражательной симметрией.
(см. Вырождение вакуума). Выбор любого из этих вакуумов приводит к теории со спонтанно нарушенной отражательной симметрией.
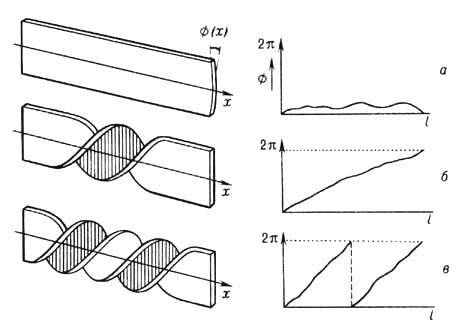
Рис. 2. Состояния полоски и отвечающие им изменения функции f(x): а- топологически тривиальная полоска с малыми отклонениями от равновесного положения; б- полоска, содержащая 2p-"скрутку"-кинк; в- полоска, содержащая 4p-"скрутку" -2-кинк.
Помимо постоянных решений ур-ние (3) допускает кинковое (антикинковое) статическое решение (рис. 3)
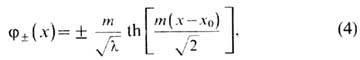
с энергией
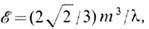 локализованной в малой окрестности точки x0. При
локализованной в малой окрестности точки x0. При  решение (4) переходит в постоянные решения, а в точке обращения в нуль параметра нелинейности l решение (4) становится сингулярным, что свидетельствует о его непертурбативном характере [т. <е. решение (4) не может быть получено методами теории возмущений].-
решение (4) переходит в постоянные решения, а в точке обращения в нуль параметра нелинейности l решение (4) становится сингулярным, что свидетельствует о его непертурбативном характере [т. <е. решение (4) не может быть получено методами теории возмущений].-

Рис. 3. Кинк (f4 -модели, локализованный в точке х =0.
Топологический заряд j4 -теории записывается в виде
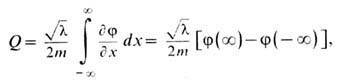
при этом Q=+1 для кинка (4) и Q=0 для постоянных решений. В классич. теории это означает, что кинк не может быть непрерывным образом деформирован ни к одному из тривиальных решений (требуется бесконечная энергия для преодоления бесконечно высокого потенц. барьера). На квантовом уровне закон сохранения топологич. заряда запрещает кинку распадаться либо посредством туннельного эффекта переходить в одно из вакуумных состояний. Все это позволяет интерпретировать кинки как устойчивые частицеподобные состояния.
Следующим важным свойством j4 -модели является наличие в ней вырожденных состояний с пространством вырождения (см. ниже) D = S0 (нульмерная сфера, состоящая, как известно, из двух точек, в данном случае
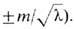 Это обстоятельство позволяет распространить как методы исследования, так и выводы j4 -модели на широкий круг объектов в физике конденсированных сред, таких, как твёрдые и жидкие кристаллы, ферромагнетики и антиферромагнетики, сверхпроводники и сверхтекучие жидкости Не 4 и Не 3 и т. д. Возможность применения топологии, методов к классификации дефектов (нарушений локального равновесия) вконденсированных средах замечена Г. E. Воловиком и В. П. Минеевым (1977) и основана на том, что во многих физически интересных ситуациях (примеры приведены ниже) можно говорить об установлении т. н. локального термодинамического равновесия. При этом можно говорить о темп-ре образца T как о ф-ции, зависящей от точки, а если состояния термодинамич. равновесия оказываются вырожденными при темп-pax ниже нек-рого кри-тич. значения T<Tc, то и др. характеристики конденсированных сред будут зависеть от точки (см. [3]). Естеств. предположение онепрерывности таких зависимостей позволяет описывать состояния конденсированных сред в терминах полевых переменных и соответственно использовать методы алгебраич. топологии (теорию гомотопий, теорию гомологии и когомологий, теорию расслоений и др.) для классификации состояний, установления закономерностей глобального характера, доказательства теорем существования солитонных решений и т. д.
Это обстоятельство позволяет распространить как методы исследования, так и выводы j4 -модели на широкий круг объектов в физике конденсированных сред, таких, как твёрдые и жидкие кристаллы, ферромагнетики и антиферромагнетики, сверхпроводники и сверхтекучие жидкости Не 4 и Не 3 и т. д. Возможность применения топологии, методов к классификации дефектов (нарушений локального равновесия) вконденсированных средах замечена Г. E. Воловиком и В. П. Минеевым (1977) и основана на том, что во многих физически интересных ситуациях (примеры приведены ниже) можно говорить об установлении т. н. локального термодинамического равновесия. При этом можно говорить о темп-ре образца T как о ф-ции, зависящей от точки, а если состояния термодинамич. равновесия оказываются вырожденными при темп-pax ниже нек-рого кри-тич. значения T<Tc, то и др. характеристики конденсированных сред будут зависеть от точки (см. [3]). Естеств. предположение онепрерывности таких зависимостей позволяет описывать состояния конденсированных сред в терминах полевых переменных и соответственно использовать методы алгебраич. топологии (теорию гомотопий, теорию гомологии и когомологий, теорию расслоений и др.) для классификации состояний, установления закономерностей глобального характера, доказательства теорем существования солитонных решений и т. д.
Дефекты в конденсированных средах как T. с. Топологич. анализ дефектов не претендует на полноту описания физ. картины, в частности, он практически не даёт количественных ответов, к-рые по сути слабо зависят от реализуемой топологии. Тем не менее такой анализ позволяет простыми средствами выявлять те качественные особенности рассматриваемых явлений, к-рые должны быть приняты во внимание при более детальном описании. Напр., легко можно понять причину отсутствия топологически устойчивых образований в обычной жидкости. Как известно, вихри могут быть устойчивы лишь в идеальной жидкости (теорема Кельвина - Гельмгольца), а под влиянием вязкости такие вихри рассасываются. С точки зрения топологии причина состоит в том, что обычная жидкость не вырождена. В то же время квантованные вихри в сверхтекучем Не 4 топологически устойчивы именно в силу вырожденности осн. состояний. В результате никакое вязкое трение не может изменить кванта циркуляции сверхтекучей скорости Не 4; с др. стороны, рассасывание вихря означало бы расширение области дефекта (нарушения сверхтекучести), что энергетически невыгодно.
Во многих случаях для предсказания существования того или иного типа дефекта в образце конденсированной среды достаточно исследовать связность п р о с т р а н с т в а в ы р о ж д е н и я D - множества всех равновесных состояний образца при фиксиров. темп-ре T. Согласно теории Ландау фазовых переходов2-го рода, равновесное состояние образца определяется минимизацией функционала свободной энергии по множеству состояний, характеризуемых конечным числом параметров, называемых параметрами порядка теории. Рассматривая параметры порядка j(x )как непрерывные отображения, определённые в области
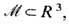 занимаемой образцом, и принимающие значения в пространстве вырождения D
занимаемой образцом, и принимающие значения в пространстве вырождения D

приходим к стандартной задаче теории гомотопий по классификации отображений (5). Математически
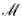 определяется как компактное связное многообразие с границей
определяется как компактное связное многообразие с границей 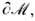 а дефекты отождествляются с особыми (сингулярными) или неособыми точками, линиями и плоскостями, где параметры порядка j(x) не определены. Если тем или иным образом удаётся доопределить отображение j(x )так, что оно будет регулярным во всей области
а дефекты отождествляются с особыми (сингулярными) или неособыми точками, линиями и плоскостями, где параметры порядка j(x) не определены. Если тем или иным образом удаётся доопределить отображение j(x )так, что оно будет регулярным во всей области  то такие дефекты наз. у с т р а н и м ы м и. Наличие неустранимых особенностей в поле параметра порядка ведёт к пересмотру его области определения, т. е. вместо (5) рассматривают отображения вида
то такие дефекты наз. у с т р а н и м ы м и. Наличие неустранимых особенностей в поле параметра порядка ведёт к пересмотру его области определения, т. е. вместо (5) рассматривают отображения вида

здесь S-область дефекта (подмногообразие
 ), где параметры j(x) не определены регулярным образом.
), где параметры j(x) не определены регулярным образом.
В том случае, когда среда обладает точечными дефектами,Sбудет 0-мерным подмногообразием, состоящим из одной или нескольких особых точек внутри
 Такие дефекты принято называть "ежами" по виду конфигурации параметра j(x) в окрестности особой точки. С топологич. точки зрения
Такие дефекты принято называть "ежами" по виду конфигурации параметра j(x) в окрестности особой точки. С топологич. точки зрения  иными словами, всегда возможно охватить область S сферой S2 (рис. 4, а), и вместо отображений (5а) рассматривать в качестве параметров порядка
иными словами, всегда возможно охватить область S сферой S2 (рис. 4, а), и вместо отображений (5а) рассматривать в качестве параметров порядка

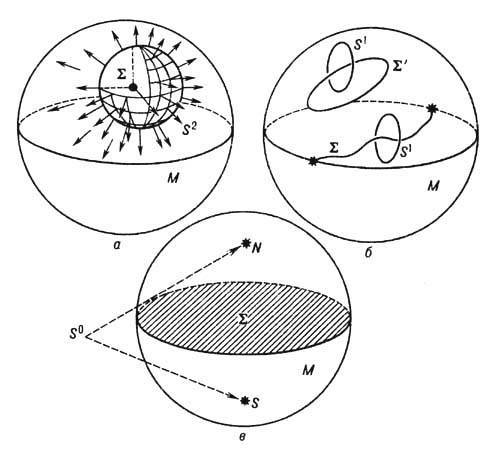
Рис. 4. Типы дефектов в конденсированных средах и соответствующие им подмногообразия дефектов S: а- точечный дефект; б- линейный дефект; в- планар ный дефект.
Дальнейшая топологич. классификация дефектов проводится по стандартной схеме. Множество отображений (6) разбивается на гомотопич. классы [S2,D]i ,
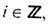 каждый из к-рых объединяет лишь те отображения из (6), к-рые переводимы друг в друга непрерывной деформацией (гомотопны между собой). Далее, на множестве гомотопич. классов
каждый из к-рых объединяет лишь те отображения из (6), к-рые переводимы друг в друга непрерывной деформацией (гомотопны между собой). Далее, на множестве гомотопич. классов  задаётся закон композиции, по отношению к к-рому классы [S2, D],· будут элементами 2-й г ом о т о п и ч е с к о й г р у п п ы p2(D) Результат анализа сводится к утверждению, что топологически стабильные точечные дефекты в конденсированных средах возможны в случае, когда
задаётся закон композиции, по отношению к к-рому классы [S2, D],· будут элементами 2-й г ом о т о п и ч е с к о й г р у п п ы p2(D) Результат анализа сводится к утверждению, что топологически стабильные точечные дефекты в конденсированных средах возможны в случае, когда  т. е. когда каждому гомотопич. классу можно поставить в соответствие нек-рое число N из бесконечной группы целых чисел
т. е. когда каждому гомотопич. классу можно поставить в соответствие нек-рое число N из бесконечной группы целых чисел 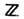 или одной из её конечных подгрупп. В применении к конденсированным средам вместо термина "гомотопический класс" употребляется термин "т о п о л о г и ч е с к и й т и п д е ф е к т а", а число N наз. т о п о л о г и ч е с к и м и н д е к с о м (или зарядом) д е ф е к т а. Др. следствием изоморфизма
или одной из её конечных подгрупп. В применении к конденсированным средам вместо термина "гомотопический класс" употребляется термин "т о п о л о г и ч е с к и й т и п д е ф е к т а", а число N наз. т о п о л о г и ч е с к и м и н д е к с о м (или зарядом) д е ф е к т а. Др. следствием изоморфизма 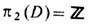 является "арифметика дефектов" при их слияниях и распадах: индекс "составного" дефекта N должен быть равен сумме (точнее, одному из значений суммы, в силу возможной многозначности операции сложения) индексов N1. и N2 слагаемых дефектов при слиянии и образовавшихся дефектов при распаде.
является "арифметика дефектов" при их слияниях и распадах: индекс "составного" дефекта N должен быть равен сумме (точнее, одному из значений суммы, в силу возможной многозначности операции сложения) индексов N1. и N2 слагаемых дефектов при слиянии и образовавшихся дефектов при распаде.
Одномерные подмногообразия дефектов S состоят из одной или нескольких особых линий, к-рые либо замкнуты в
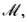 либо начинаются и заканчиваются на границе
либо начинаются и заканчиваются на границе 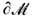 (рис. 4, б). Такие линейные дефекты наз. "вихрями" или "струнами", а область S в любой точке можно охватить окружностью S1. В этом случае параметры порядка суть отображения
(рис. 4, б). Такие линейные дефекты наз. "вихрями" или "струнами", а область S в любой точке можно охватить окружностью S1. В этом случае параметры порядка суть отображения
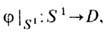
гомотопич. классы [S1, D]i будут элементами 1-й г о м от о п и ч е с к о й (ф у н д а м е н т а л ь н о й) г р у п п ы p1(D). Для существования топологически стабильных линейных дефектов требуется наличие изоморфизма
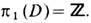 Наконец, когда dimS=2 мы приходим к параметрам порядка типа
Наконец, когда dimS=2 мы приходим к параметрам порядка типа
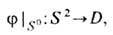
характерных для среды с планарными дефектами типа "доменных стенок" (рис. 4, в). Классификация проводится на основе т. н. 0-й г о м о т о п и ч е с к о й г р у п п ы p0(D )и критеоий существования стабильных планарных дефектов
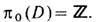 Т. <о., дефекты в конденсированных средах возникают как локализованные в пространстве структуры с нетривиальными топологич. характеристиками - и н д ек с а м и N, аих стабильность обеспечивается топологией пространства вырождения. Это и является основанием для рассмотрения перечисленных дефектов как Т. <е. (в расширенном смысле). Следует отметить, что T. с. в теории поля, как правило, обладают регулярным поведением во всей области определения.
Т. <о., дефекты в конденсированных средах возникают как локализованные в пространстве структуры с нетривиальными топологич. характеристиками - и н д ек с а м и N, аих стабильность обеспечивается топологией пространства вырождения. Это и является основанием для рассмотрения перечисленных дефектов как Т. <е. (в расширенном смысле). Следует отметить, что T. с. в теории поля, как правило, обладают регулярным поведением во всей области определения.
На языке топологии получает естеств. объяснение и наиб. известный линейный дефект в кристаллах - краевая дислокация, возникающая при образовании лишней кристаллич. полуплоскости в решётке (рис. 5). Предполагается, что на расстояниях в несколько постоянных решётки от линии AB кристаллич. порядок восстанавливается. Поскольку пространство вырождения не зависит от вида кристалла, то достаточно рассмотреть простейший кубич. кристалл и смещения лишь вдоль одной из осей, х, с периодом решётки а х. Состояния кристалла вырождены относительно сдвигов на а х, т. к. такой сдвиг приводит к совмещению кристалла с самим собой. Иными словами, концы отрезка [0, а х]отвечают одному и тому же состоянию, что позволяет их отождествить. Для смещений х, лежащих вне отрезка [0, а х], всегда найдётся эквивалентное смещение внутри того же отрезка. В результате приходим к пространству вырождения кристалла по оси х ввиде отрезка [0, а х] с отождествлёнными концами, что топологически эквивалентно окружности S1. Аналогичное вырождение состояний наблюдается и вдоль осей у и z, т. е. пространством вырождения кристалла в целом будет
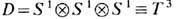 - многообразие трёхмерного тора.
- многообразие трёхмерного тора.
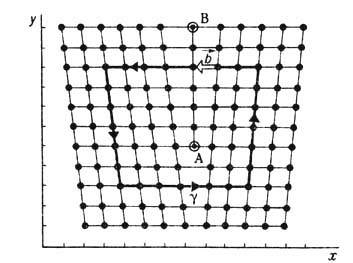
Рис. 5. Краевая дислокация в кубическом кристалле с осями вдоль x, y и z. Линия дислокации, которая перпен дикулярна плоскости рисунка и изображена точкой А, является краем лишней полуплоскости. Замкнутый контур g отвечает обходу линии дислокации в положительном направлении. Дислокация характеризуется топологически ми индексами Nx=1, Ny=Nz=0и вектором Бюргерса b = а х е х, перпендикулярным линии дислокации.
Топологич. тип параметров порядка кристалла (в соответствии с приведённой выше схемой) будет характеризоваться группой
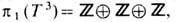 т. е. топологически устойчивые дисклинации в кристаллах обладают тремя целочисленными топологич. индексами Nx, Ny и Nz, каждый из к-рых сохраняется при распадах и слияниях дислокаций. Отметим, что закон сохранения трёх индексов Ni , i = х, у, z, эквивалентен закону сохранения вектора Бюр- герса
т. е. топологически устойчивые дисклинации в кристаллах обладают тремя целочисленными топологич. индексами Nx, Ny и Nz, каждый из к-рых сохраняется при распадах и слияниях дислокаций. Отметим, что закон сохранения трёх индексов Ni , i = х, у, z, эквивалентен закону сохранения вектора Бюр- герса 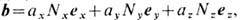 где еi - орт в направлении i- той оси. Поскольку топологич. тип линии дислокации не изменяется при непрерывных деформациях, то приведённый результат полностью переносится и на винтовые дислокации, к-рые топологически эквивалентны краевым. В изотропном ферромагнетике пространством вырождения является двумерная сфера D = S2. Действительно, при Т < Т C (точка Кюри) в ферромагнетике возникает спонтанная намагниченность с вектором намагниченности M, длина к-рого фиксируется темп-рой образца: |M|=M(T) Энергия ферромагнетика может зависеть как от величины M (собственно магн. энергия), так и от направления вектора M (т. н. энергия магнитной анизотропии). Поскольку энергия магн. анизотропии, как правило, пренебрежимо мала по сравнению с чисто магн. энергией, то для одного и того же энергетич. состояния ферромагнетика вектор M при заданной T может принимать все возможные направления. Каждому направлению нормированного на единицу вектора n=M(T)/M(T) (параметр порядка ферромагнетика) можно взаимно однозначно сопоставить точку на сфере S2 (последняя возникает как геом. место точек - концов вектора n). Следовательно, в изотропных магнети-ках с D = S2 могут существовать стабильные точечные дефекты ("ежи"), т. к.
где еi - орт в направлении i- той оси. Поскольку топологич. тип линии дислокации не изменяется при непрерывных деформациях, то приведённый результат полностью переносится и на винтовые дислокации, к-рые топологически эквивалентны краевым. В изотропном ферромагнетике пространством вырождения является двумерная сфера D = S2. Действительно, при Т < Т C (точка Кюри) в ферромагнетике возникает спонтанная намагниченность с вектором намагниченности M, длина к-рого фиксируется темп-рой образца: |M|=M(T) Энергия ферромагнетика может зависеть как от величины M (собственно магн. энергия), так и от направления вектора M (т. н. энергия магнитной анизотропии). Поскольку энергия магн. анизотропии, как правило, пренебрежимо мала по сравнению с чисто магн. энергией, то для одного и того же энергетич. состояния ферромагнетика вектор M при заданной T может принимать все возможные направления. Каждому направлению нормированного на единицу вектора n=M(T)/M(T) (параметр порядка ферромагнетика) можно взаимно однозначно сопоставить точку на сфере S2 (последняя возникает как геом. место точек - концов вектора n). Следовательно, в изотропных магнети-ках с D = S2 могут существовать стабильные точечные дефекты ("ежи"), т. к. 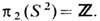 В то же время линейные и планарные дефекты в таком магнетике будут неустойчивы. При наложении однородных граничных условий на бесконечности (n = n0 при
В то же время линейные и планарные дефекты в таком магнетике будут неустойчивы. При наложении однородных граничных условий на бесконечности (n = n0 при 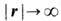 ) возникает эфф. компак-тификация пространства R3 т. е.
) возникает эфф. компак-тификация пространства R3 т. е. 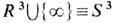 .В результате вместо (5) имеем о т о б р а ж е н и я Х о п ф а (Н. Hopf):
.В результате вместо (5) имеем о т о б р а ж е н и я Х о п ф а (Н. Hopf):
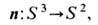
классифицирующиеся по группе
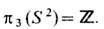
Простейшей нетривиальной конфигурацией поля в таком случае будет неособый кольцевой вихрь с инвариантом Хопфа QH=1 Правда, для стабилизации такого вихря к лагранжиану обычной сигма-модели требуется добавить члены 4-го порядка по производным n [4].
Для анизотропного ферромагнетика типа "лёгкая плоскость" вектор n лежит в нек-рой плоскости, и пространством вырождения в этом случае будет D = S1 (окружность). В таких образцах могут возникать устойчивые линейные дефекты - "вихри", т. к.
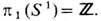 В полярных координатах (r, j) на плоскости вне области дефекта S параметр порядка можно представить в виде
В полярных координатах (r, j) на плоскости вне области дефекта S параметр порядка можно представить в виде 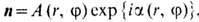 , где a(r, j)-непрерывно меняющаяся фаза (угол между направлением M и нек-рым фиксиров. направлением в "лёгкой плоскости"). "Вихрем" будет такая особая линия, при обходе к-рой фаза меняется на
, где a(r, j)-непрерывно меняющаяся фаза (угол между направлением M и нек-рым фиксиров. направлением в "лёгкой плоскости"). "Вихрем" будет такая особая линия, при обходе к-рой фаза меняется на 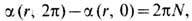 где N -т о п о л о г и ч е с к и й и н в а р и а н т "в и х р я" - целое число, показывающее, сколько полных оборотов при этом делает вектор n. На рис. 6, a изображён вихрь с N= 1, на рис. 6, б -с N = - 1, 6,в - с N = 0.
где N -т о п о л о г и ч е с к и й и н в а р и а н т "в и х р я" - целое число, показывающее, сколько полных оборотов при этом делает вектор n. На рис. 6, a изображён вихрь с N= 1, на рис. 6, б -с N = - 1, 6,в - с N = 0.
Наконец, в ферромагнетиках типа "лёгкая ось" равновесными пpи каждом значении T будут лишь два состояния M=+Mu (где u -единичный вектор в направлении "лёгкой оси" намагничивания), т. е. D = S0. В силу того, что p0(S0) =Z, можно говорить о допустимости T. с. типа "доменных стенок" в магнетиках типа "лёгкая ось". Динамика простейших "доменных стенок" описывается синус-Гордона ур-нием, Шрёдингера уравнением нелинейным и т. д. ([5], [6]).
Параметром порядка в нематических жидких кристаллах (или нематиках) служит директор d, указывающий преимущественное направление длинных осей вытянутых молекул нематика при нек-рой Т<Т C (в отличие от вектора n, для директора направления d и - d физически неразличимы). [Название "нематик" предложено Ш. Фриделем (Ch. Friedel). ] Областью вырождения D (областью значений директора d )в трёхмерном нематике является вещественное проективное пространство RP2. (получаемое из сферы S2 отождествлением диаметрально противоположных точек). Соответственно допустимы стабильные точечные особенности ("ежи"), к-рые классифицируются группой
 а их конфигурации и "арифметика" те же, что и для точечных дефектов в изотропном магнетике. Линейные дефекты - дисклинации в трёхмерном немати-ке - характеризуются группой
а их конфигурации и "арифметика" те же, что и для точечных дефектов в изотропном магнетике. Линейные дефекты - дисклинации в трёхмерном немати-ке - характеризуются группой 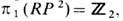 где
где  - подгруппа
- подгруппа 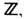 задающая "двоичную арифметику" топологич. инвариантов дисклинации: 0 + 1 = 1; 1 + 1=0. В связи с этим устойчивыми будут лишь дисклинации с нечётным топологич. инвариантом - индексом Франка NF (рис. 6, г, д, е), а дисклинации с чётным индексом NF (рис. 6, а, б )будут неустойчивы, т. к. они имеют возможность "вытекать в третье измерение". И н д е к с Ф р а н к а определяется по аналогии с др. топологич. инвариантами как целое число NF, связанное с изменением фазы a вектора d при обходе по замкнутому контуру вокруг линии дисклинации соотношением a=pNF Заметим, что дисклинации, изображённые на рис. 6 ( г, д, е ), невозможны в ферромагнетиках, т. к. при этом поле n имело бы разрыв вдоль поверхности, опирающейся на особую линию. В нематиках они существуют лишь в силу неразличимости взаимно противоположных направлений директора d. B двумерных нематиках
задающая "двоичную арифметику" топологич. инвариантов дисклинации: 0 + 1 = 1; 1 + 1=0. В связи с этим устойчивыми будут лишь дисклинации с нечётным топологич. инвариантом - индексом Франка NF (рис. 6, г, д, е), а дисклинации с чётным индексом NF (рис. 6, а, б )будут неустойчивы, т. к. они имеют возможность "вытекать в третье измерение". И н д е к с Ф р а н к а определяется по аналогии с др. топологич. инвариантами как целое число NF, связанное с изменением фазы a вектора d при обходе по замкнутому контуру вокруг линии дисклинации соотношением a=pNF Заметим, что дисклинации, изображённые на рис. 6 ( г, д, е ), невозможны в ферромагнетиках, т. к. при этом поле n имело бы разрыв вдоль поверхности, опирающейся на особую линию. В нематиках они существуют лишь в силу неразличимости взаимно противоположных направлений директора d. B двумерных нематиках 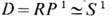 и отсутствуют устойчивые точечные дефекты в силу p2(RP2)=0 В то же время в них реализуются как устойчивые структуры все типы дисклинации, изображённые на рис. 6, т. к.
и отсутствуют устойчивые точечные дефекты в силу p2(RP2)=0 В то же время в них реализуются как устойчивые структуры все типы дисклинации, изображённые на рис. 6, т. к. 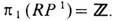 Топологич. анализ дефектов в антиферромагнетиках проводится по аналогии с нематиками.
Топологич. анализ дефектов в антиферромагнетиках проводится по аналогии с нематиками. 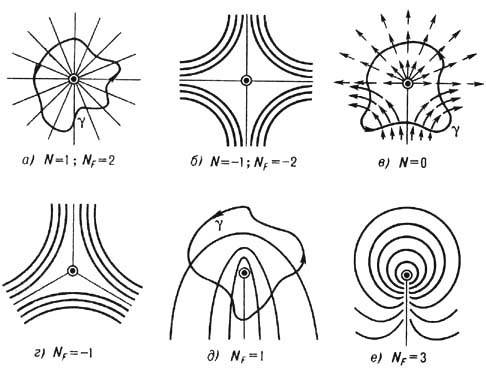
Рис. 6. Вихревые дефекты в ферромагнетиках и дискли нации в нематиках (во всех случаях особые линии пер пендикулярны плоскости рисунков).
Для сверхтекучей компоненты Не 4 (см. Гелий жидкий, Квантовая жидкость )областью вырождения D состояний, описываемых волновой ф-цией y=|y|exp(ij) будет область возможных значений волновой ф-ции при фиксированном её модуле |y|. Физически это связано с т. н. Базе - Эйнштейна конденсацией бесспиновых атомов изотопа Не 4 в состоянии с наим. энергией жидкости при темп-ре Т<Т C, т. е. с накоплением в одном и том же состоянии большого числа частиц квантовой жидкости. Если пренебречь слабым взаимодействием между атомами жидкости, то при T=0 oK в состоянии с мин. энергией будут находиться все без исключения частицы, что и позволяет описывать их одной и той же (не зависящей от координат частиц) волновой ф-цией y=|y|exp(ij). Нормированная волновая ф-ция Ф(x)=(y/|y|)ехр[ij(x)] в этом случае играет роль параметра порядка, т. е. на комплексной плоскости, область вырождения представляет собой окружность D = S1, вдоль к-рой меняется фаза j (вырождение состояний по фазе). На основании того, что
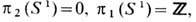 заключаем, что точечных дефектов в Не 4 нет; в то же время линейные дефекты - вихри в Не 4 - будут устойчивыми особенностями с целочисленными топологич. инвариантами.
заключаем, что точечных дефектов в Не 4 нет; в то же время линейные дефекты - вихри в Не 4 - будут устойчивыми особенностями с целочисленными топологич. инвариантами.
Действительно, скорость течения сверхтекучей компоненты Не 4 выражается через градиент фазы
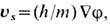 где m - масса атома Не 4. Циркуляция скорости выражается через изменение фазы dj при обходе линии вихря по произвольному замкнутому контуру g и равна
где m - масса атома Не 4. Циркуляция скорости выражается через изменение фазы dj при обходе линии вихря по произвольному замкнутому контуру g и равна 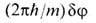 Однозначной волновая ф-ция F будет лишь при условии, что изменение фазы
Однозначной волновая ф-ция F будет лишь при условии, что изменение фазы 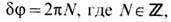 т. е. имеет место квантование циркуляции скорости при обходе вокруг линии вихря. Поскольку dj=2pN при обходе по любому сколь угодно малому контуру g, это означает, что сама фаза не может быть однозначно определена на линии вихря, т. е. это действительно особая линия. Именно в силу квантования циркуляции интенсивность вихря лишена возможности уменьшаться непрерывным образом под действием вязкости. С др. стороны, запрещено возникновение вихрей с произвольной циркуляцией. Всё это и обеспечивает незатухающий характер сверхтекучего движения в Не 4. Значению N =0 соответствуют безвихревые, или потенциальные, течения Не 4. Топологич. свойства сверхпроводников совпадают со свойствами сверхтекучего Не 4.
т. е. имеет место квантование циркуляции скорости при обходе вокруг линии вихря. Поскольку dj=2pN при обходе по любому сколь угодно малому контуру g, это означает, что сама фаза не может быть однозначно определена на линии вихря, т. е. это действительно особая линия. Именно в силу квантования циркуляции интенсивность вихря лишена возможности уменьшаться непрерывным образом под действием вязкости. С др. стороны, запрещено возникновение вихрей с произвольной циркуляцией. Всё это и обеспечивает незатухающий характер сверхтекучего движения в Не 4. Значению N =0 соответствуют безвихревые, или потенциальные, течения Не 4. Топологич. свойства сверхпроводников совпадают со свойствами сверхтекучего Не 4.
Ситуация с топологически стабильными дефектами в Не 3 более сложная, т. к. параметром порядка в этом случае является комплексный тензор 2-го ранга Aik , i, k =1,2, 3. Это, в частности, есть отражение того факта, что в отличие от бозе-жидкости Не 4, Не 3 является ферми-жидкостью, допускающей существование анизотропных сверхтекучих фаз. Для B -фазы Не 3 пространство вырождения D топологически эквивалентно
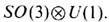 Вычисления гомотопич. групп p2(D)=0
Вычисления гомотопич. групп p2(D)=0 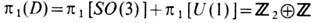 указывают на то, что в B -фазе Не 3 отсутствуют топологически стабильные точечные дефекты, а линейные дефекты - вихри - характеризуются набором из двух топологич. чисел.
указывают на то, что в B -фазе Не 3 отсутствуют топологически стабильные точечные дефекты, а линейные дефекты - вихри - характеризуются набором из двух топологич. чисел.
Для A -фазы Не 3 пространство
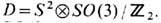 Это означает, что пространство
Это означает, что пространство 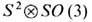 -двулистное накрытие D, а, следовательно, односвязное пространство
-двулистное накрытие D, а, следовательно, односвязное пространство 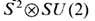 - четырёхлистное накрытие D. В итоге для гомотопич. групп пространства вырождения параметра порядка A -фазы имеем
- четырёхлистное накрытие D. В итоге для гомотопич. групп пространства вырождения параметра порядка A -фазы имеем 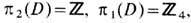 т. е. в A- фазе Не 3 точечные дефекты характеризуются целочисленным топологич. инвариантом, а для вихрей топологич. инвариант будет вычетом по модулю 4. Подобная структура фаз и топология дефектов предполагается и в нейтронных звёздах.
т. е. в A- фазе Не 3 точечные дефекты характеризуются целочисленным топологич. инвариантом, а для вихрей топологич. инвариант будет вычетом по модулю 4. Подобная структура фаз и топология дефектов предполагается и в нейтронных звёздах.
Динамика многомерных T. с. Топологич. анализ дефектов даёт лишь качественные ответы и необходимые критерии существования стабильных T. с. типа наличия изоморфизмов pk(D)=Z для пространств вырождения параметров порядка. При этом в роли параметров порядка могут фигурировать скалярные, комплексные, векторные и в общем случае тензорные поля. Количественное описание T. с. основывается на построении, как правило, нелинейных динамич. моделей, обладающих след. свойствами: (а) ур-ния Эйлера - Лагранжа модели допускают регулярные локализованные решения с конечными динамич. характеристиками (энергией, импульсом, моментом импульса и т. д.); (б) состояния наделены нетривиальными топологич. характеристиками Q (зарядами, индексами и т. д.); (в) функционал энергии модели оценивается снизу через топологич. инвариант
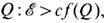 с = const, что обеспечивает динамич. устойчивость T. с.
с = const, что обеспечивает динамич. устойчивость T. с.
В и х р и Н и л ь с е н а - О л е с е н а (H. В. Nielsen, P. Оlеsen, 1973). Динамич. описание линейных дефектов типа вихря возможно, напр., в рамках т. н. абелевой калибровочной модели Хиггса (P. W. Higgs, 1964; см. Хиггса механизм )с калибровочной группой U(1) и лагранжианом

где
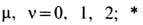 означает комплексное сопряжение,
означает комплексное сопряжение, 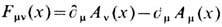 - тензор напряжённости эл.-магн. поля,
- тензор напряжённости эл.-магн. поля, 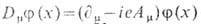 - ковариантная производная, a0 = const. Комплексное хиггсовское поле
- ковариантная производная, a0 = const. Комплексное хиггсовское поле 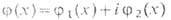 можно рассматривать, напр., как параметр порядка сверхпроводящей среды, а пространство вырождения в этом случае совпадает с многообразием классич. вакуумов |j|2=a20, т. е. D=S1, На этом основании можно предположить наличие стабильных T. с. типа вихрей, т. к.
можно рассматривать, напр., как параметр порядка сверхпроводящей среды, а пространство вырождения в этом случае совпадает с многообразием классич. вакуумов |j|2=a20, т. е. D=S1, На этом основании можно предположить наличие стабильных T. с. типа вихрей, т. к. 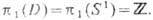 Ур-ния Эйлера - Лагран-жа для (7)
Ур-ния Эйлера - Лагран-жа для (7)
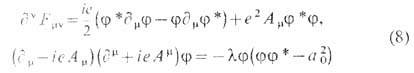
действительно допускают вихревые решения, т. н. вихри Нильсена - Олесена, на статических цилиндрически-симметричных полевых конфигурациях
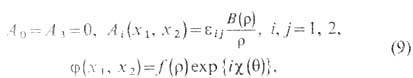
где
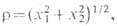 q=arctg(x2/x1). Естественное условие отсутствия токов на бесконечности
q=arctg(x2/x1). Естественное условие отсутствия токов на бесконечности 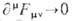 при
при 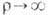 влечёт в силу (8) и (9)
влечёт в силу (8) и (9)  В результате магн. поток F через плоскость (x1, x2 )запишется как
В результате магн. поток F через плоскость (x1, x2 )запишется как
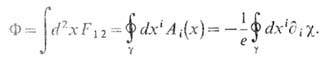
Требование однозначной определённости поля Хиггса j выполнено тогда (и только тогда), когда при обходе линии вихря по любому замкнутому контуру g фаза c изменяется на 2pN, следовательно,
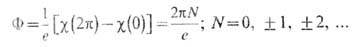
В результате магн. поток оказывается квантованным (без привлечения к.-л. постулата о квантовании) с квантом потока 2p/e. Аналогичное свойство присуще вихрям магн. потока в сверхпроводниках 2-го рода (см. Решётка вихрей Абрикосова )(с заменой
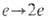 в силу Купера эффекта), т. к. в статическом пределе абелева модель Хиггса сводится к Гинзбурга- Ландау теории сверхпроводимости [7].
в силу Купера эффекта), т. к. в статическом пределе абелева модель Хиггса сводится к Гинзбурга- Ландау теории сверхпроводимости [7].
Вихри с N квантами магн. потока описываются решениями вида (9) ур-ний (8), к-рые при c=Nq удовлетворяют системе обыкновенных дифференц. ур-ний:
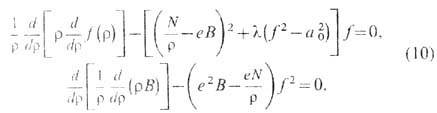
Из требования конечности энергии, приходящейся на единицу длины вихря, выводится асимптотич. поведение ф-ций f(r) и B(r) на пространственной бесконечности:
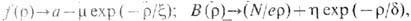 где m,
где m,
h-константы,
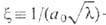 -длина когерентности, задающая масштаб изменений скалярного поля,
-длина когерентности, задающая масштаб изменений скалярного поля, 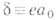 - глубина проникновения (характерный масштаб для магн. поля), T. о., вне линии вихря f(r) и B(r) экспоненциально убывают с увеличением расстояния. Помимо точного (чисто калибровочного) решения f(r)=a0,
- глубина проникновения (характерный масштаб для магн. поля), T. о., вне линии вихря f(r) и B(r) экспоненциально убывают с увеличением расстояния. Помимо точного (чисто калибровочного) решения f(r)=a0,
B(r)=(N/er) известны лишь численные решения ур-ний (10). По величине безразмерного параметра Гинзбурга - Ландау
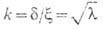 свеохпооводники можно разбить на два класса: условием
свеохпооводники можно разбить на два класса: условием 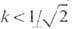 выделяются сверхпроводники первого рода; при
выделяются сверхпроводники первого рода; при 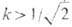 имеем сверхпроводники второго рода. Устойчивые вихри характерны лишь для сверхпроводников 2-го рода, т. к. при
имеем сверхпроводники второго рода. Устойчивые вихри характерны лишь для сверхпроводников 2-го рода, т. к. при 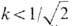 между вихрями возникают силы притяжения, под действием к-рых они коллапсируют. Напротив, при
между вихрями возникают силы притяжения, под действием к-рых они коллапсируют. Напротив, при 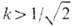 между вихрями возникают силы отталкивания, приводящие к образованию треугольных решёток с единичными (несущими один квант магн. потока) вихрями в узлах. Поскольку при
между вихрями возникают силы отталкивания, приводящие к образованию треугольных решёток с единичными (несущими один квант магн. потока) вихрями в узлах. Поскольку при 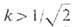 энергия (на единицу длины) N -вихревой конфигурации
энергия (на единицу длины) N -вихревой конфигурации 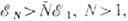 где
где 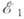 -энергия (на единицу длины) единичного вихря, то такая конфигурация оказывается неустойчивой и распадается на N отдельных единичных вихрей, что и подтверждается экспериментом. (В сверхтекучих жидкостях, по аналогичным причинам, устойчивыми и наблюдаемыми являются лишь вихри с единичным топологическим числом.) В случае
-энергия (на единицу длины) единичного вихря, то такая конфигурация оказывается неустойчивой и распадается на N отдельных единичных вихрей, что и подтверждается экспериментом. (В сверхтекучих жидкостях, по аналогичным причинам, устойчивыми и наблюдаемыми являются лишь вихри с единичным топологическим числом.) В случае 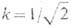 ур-ния (10) редуцируются к системе 1-го порядка:
ур-ния (10) редуцируются к системе 1-го порядка:
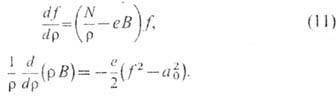
Из (11) для энергии N -вихря, т. <е. вихря, несущего N квантов магн. потока, выводится следующее выражение через энергию единичного вихря:
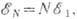 что свидетельствует об
что свидетельствует об 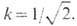 отсутствии взаимодействия между вихрями при
отсутствии взаимодействия между вихрями при
В и х р и Б е л а в и н а - П о л я к о в а (А. А, Белавин, A. M. Поляков, 1975) - T. с., обнаруженные в т. н. нелинейной O(3)-модели n -поля n(x, t){na(x,t), a=1, 2, 3;
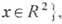 где п a - действительные скалярные поля, подчинённые условию
где п a - действительные скалярные поля, подчинённые условию
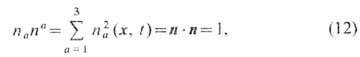
т. <е. со значениями на сфере S2. Динамика модели задаётся лагранжианом
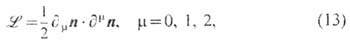
и ур-нием связи (12). Ур-ния Эйлера - Лагранжа находятся как условие экстремума действия для (13), где связь (12) учтена введением множителя Лагранжа, в итоге для статических полей имеем
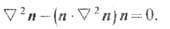
Состояния с нулевой статической энергией
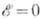 ("классич. вакуумы"), где
("классич. вакуумы"), где
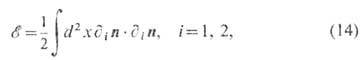
получаются из условия д in=0 т. <е. для всех
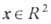 поле n(x) =n0 где n0 - нек-рый фиксированный единичный вектор с произвольной ориентацией. Иными словами, модель содержит вырожденное непрерывное семейство "классич. вакуумов", переводимых друг в друга преобразованиями (вращениями) из группы O(3), т. <е. пространство вырождения D=S2. Солитонные решения с ненулевой, но конечной энергией (14) - T. с.- должны удовлетворять граничным условиям
поле n(x) =n0 где n0 - нек-рый фиксированный единичный вектор с произвольной ориентацией. Иными словами, модель содержит вырожденное непрерывное семейство "классич. вакуумов", переводимых друг в друга преобразованиями (вращениями) из группы O(3), т. <е. пространство вырождения D=S2. Солитонные решения с ненулевой, но конечной энергией (14) - T. с.- должны удовлетворять граничным условиям
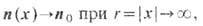
в силу к-рых пространство R2 пополняется бесконечно удалёнными точками и эффективно компактифицируется
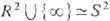 , т. е. T. с. следует искать среди отображений п( х):
, т. е. T. с. следует искать среди отображений п( х): . Такие отображения классифицируются группой
. Такие отображения классифицируются группой 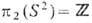 с определённым значением топологич. заряда
с определённым значением топологич. заряда
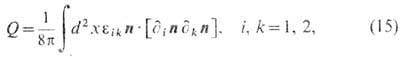
где скалярное и векторное произведения относятся к векторам n, eik - Леви-Чивиты символ. Из тождества
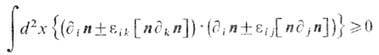
с учётом (14), (15) находится оценка для энергии T. с.:

обеспечивающая его устойчивость в каждом гомотопич. классе. В случае равенства в (16) минимум энергии (14) реализуется на решениях т. <н. ур-ний Богомольного (E. Б. Богомольный, 1976)

к-рые в координатах стереографич. проекции
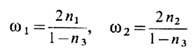
представляют собой условия Коши - Римана:
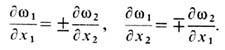
T. о., любая аналитическая функцияw(z )или w(z*) где
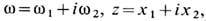 записанная в переменных п a и х, удовлетворяет ур-ниям (17). Напр.,
записанная в переменных п a и х, удовлетворяет ур-ниям (17). Напр.,
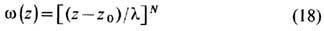
описывает T. с. нелинейной O(3)-модели с топологии, зарядом Q=N т. <н. N- вихри Белавина - Полякова. Здесь l -любое действительное число, n - любое положительное целое число, z0 - произвольное комплексное число. Считая поле n спиновой переменной, нелинейную O(3)-модель можно рассматривать как вариант Гейзенберга модели планарного магнетика. Статические решения (18) в (2+1)-измерениях переносятся и на случай O(3)-модели в (1+1)-измерениях, где они реализуются как инстантоны[1]. В (3+1) измерениях для возможных Т. <е.- неособых кольцевых вихрей с единичным индексом Хопфа - при выборе функционала энергии
 в виде (14) не имеет места оценка (16) и
в виде (14) не имеет места оценка (16) и 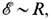 где R - радиус кольца. Следовательно, минимум энергии достигается при
где R - радиус кольца. Следовательно, минимум энергии достигается при 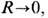 что свидетельствует о нестабильности кольцевого вихря. Ситуация исправляется, напр., добавлением в (13) членов более высокого порядка по градиентам n -поля.
что свидетельствует о нестабильности кольцевого вихря. Ситуация исправляется, напр., добавлением в (13) членов более высокого порядка по градиентам n -поля.
Т о р о н ы Р ы б а к о в а (Ю. П. Рыбаков, 1981) - T. с. в виде замкнутых "закрученных" струн с нетривиальным индексом Хопфа-реализуются в т. <н. модели Фаддеева (Л. Д. Фаддеев, 1973) для n -поля в (3+1)-измерениях, где n(x, t )-поле определено на
 и подчинено условиям
и подчинено условиям
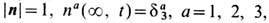 в силу к-рых его можно представить как отображение
в силу к-рых его можно представить как отображение 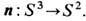 Соответственно n -полевые конфигурации классифицируются элементами группы
Соответственно n -полевые конфигурации классифицируются элементами группы 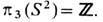 Лагранжиан модели
Лагранжиан модели
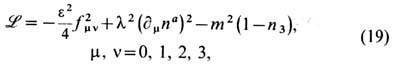
где e,l,m -постоянные параметры,
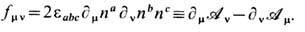
Массовый член т 2 (1- n3) добавляется в (19) для обеспечения требуемого асимптотич. поведения полей на бесконечности. Топологич. инвариант модели - индекс Хопфа QH вычисляется по ф-ле
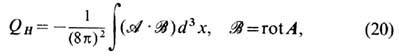
и для энергии имеет место оценка
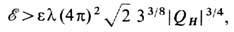
обеспечивающая стабильность неособых вихрей в рамках модели Фаддеева (19). Минимум энергии реализуется на аксиально-симметричной конфигурации (тороне), к-рую удобно записывать в угловых переменных b, g на S2: b=b(r, z), g=la+u(r, z), где l -целое число, r, a, z - цилиндрич. координаты, u(r, z) -нек-рая новая переменная, и для регулярных решений
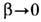 при
при 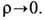 Это свидетельствует о тороидальной структуре T. с. в модели Фаддеева, представляющих собой замкнутые "закрученные" струны (или неособые кольцевые вихри). Математически существование таких T. с. доказано, однако не известно ни одного точного решения ур-ний поля модели. Подобные локализованные структуры возникают в изотропных маг-нетиках, в физике элементарных частиц (модель тяжёлых мезонов), в астрофизике и т. д. [8].
Это свидетельствует о тороидальной структуре T. с. в модели Фаддеева, представляющих собой замкнутые "закрученные" струны (или неособые кольцевые вихри). Математически существование таких T. с. доказано, однако не известно ни одного точного решения ур-ний поля модели. Подобные локализованные структуры возникают в изотропных маг-нетиках, в физике элементарных частиц (модель тяжёлых мезонов), в астрофизике и т. д. [8].
М о н о п о л и т Х о о ф т а - П о л я к о в а (G. 't Hooft, A. M. Поляков, 1974) возникают как T. с. в (3+1) измерениях при обобщении калибровочной модели Хиггса (7) на случай неабелевой калибровочной группы, напр. группы SU(2 )(см. Магнитный монополь, Калибровочные поля). Лагранжиан выбирается в виде (7) со след. изменениями:
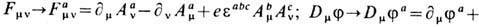
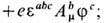 вместо комплексного рассматривается изо-векторное хиггсовское поле fa(x), а =1, 2,3. Т.c. реализуются как сферически-симметричные статические конфигурации вида
вместо комплексного рассматривается изо-векторное хиггсовское поле fa(x), а =1, 2,3. Т.c. реализуются как сферически-симметричные статические конфигурации вида
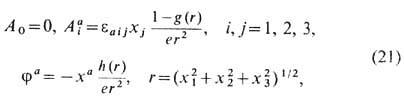
где ф-ции g (r), h (r )находятся как решения системы:
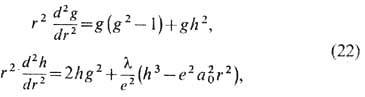
отвечающие след. поведению калибровочного Aai и изовек-торного ja полей на границе R3:
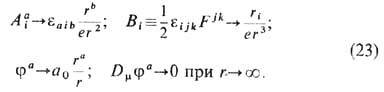
Выбор нетривиальных условий (23), с одной стороны, обеспечивает конечность энергии
 с другой - позволяет полям ja(x) принимать разл. направления (во внутр. изото-пич. пространстве, см. Изотопическая инвариантность )в бесконечно удалённых точках, т. к.
с другой - позволяет полям ja(x) принимать разл. направления (во внутр. изото-пич. пространстве, см. Изотопическая инвариантность )в бесконечно удалённых точках, т. к.  Поскольку граница пространства R3 может быть отождествлена с "пространственной" сферой S2, а поля
Поскольку граница пространства R3 может быть отождествлена с "пространственной" сферой S2, а поля 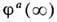 принимают значения на "полевой" сфере S2, то естественно рассматривать их как регулярные отображения, классифицируемые группой
принимают значения на "полевой" сфере S2, то естественно рассматривать их как регулярные отображения, классифицируемые группой 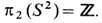 Топологич. инвариант модели в этом случае связан с магн. зарядом монополя, что подтверждается с помощью калибровочно инвариантного тензора эл.-магн. поля т' Хоофта
Топологич. инвариант модели в этом случае связан с магн. зарядом монополя, что подтверждается с помощью калибровочно инвариантного тензора эл.-магн. поля т' Хоофта
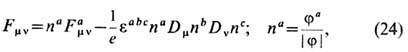
к-рый на конфигурации (21) равен
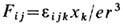 , а магн. поле
, а магн. поле 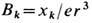 в точности совпадает с полем точечного монополя с магн. зарядом qm=1/e. В отличие от электродинамики Максвелла тензор (24) имеет дуальный тензор с ненулевой дивергенцией и, как следствие,
в точности совпадает с полем точечного монополя с магн. зарядом qm=1/e. В отличие от электродинамики Максвелла тензор (24) имеет дуальный тензор с ненулевой дивергенцией и, как следствие,
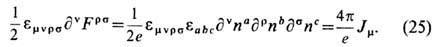
Видно, что (1/e)Jm имеет смысл магн. тока, в то время как Jm- топологич. ток. Действительно, из (25) следует, что магн. поле В подчиняется ур-нию
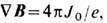 откуда по теореме Гаусса - Остроградского получаем соотношение между топологич. инвариантом Q [для отображений из
откуда по теореме Гаусса - Остроградского получаем соотношение между топологич. инвариантом Q [для отображений из 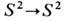 он наз. и н д е к с о м К р о н е к е р а (L. Kronecker)] и магнитным монопольным зарядом
он наз. и н д е к с о м К р о н е к е р а (L. Kronecker)] и магнитным монопольным зарядом 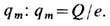 T. о., магн. заряд монополя имеет топологич. природу, а его квантование возникает как чисто классич. эффект [1], [2], [7].
T. о., магн. заряд монополя имеет топологич. природу, а его квантование возникает как чисто классич. эффект [1], [2], [7].
Точные решения системы (22) известны лишь для одиночного монополя в пределе
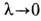 -т. <н. пределе Прасада-Соммерфилда (M. К. Prasad, C. H. Sommerfield, 1975), при фиксированных e, a0, и равны:
-т. <н. пределе Прасада-Соммерфилда (M. К. Prasad, C. H. Sommerfield, 1975), при фиксированных e, a0, и равны:
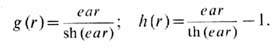
В этом пределе для энергии модели справедлива оценка и равенство в (26) достигается на решениях ур-ний Богомольного
 описывающих конфигурации с мин. энергией при любом значении Q. Из (26) следует, что монополи должны обладать массой
описывающих конфигурации с мин. энергией при любом значении Q. Из (26) следует, что монополи должны обладать массой 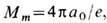 к-рая растёт с уменьшением константы взаимодействия е и по оценкам должна быть порядка 1016 ГэВ. При
к-рая растёт с уменьшением константы взаимодействия е и по оценкам должна быть порядка 1016 ГэВ. При 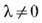 возможность существования T. с. подтверждена лишь прямыми вариационными методами (Ю. С. Тюпкин, В. А. Фатеев, А. С. Шварц, 1976) и численными расчётами. Помимо монопольных решений модель допускает т. н. д и о н ы Джулиа - Зи (В. Julia, A. Zee, 1975), т. <е. объекты с электрическим и магнитным зарядами. Физически монополи предсказываются теорией Великого объединения и могут выступать в роли катализатора распада протона - эффект Каллана - Рубакова (В. А. Рубаков, 1981; С. G. Callan, 1982), но до сих пор не обнаружены экспериментально.
возможность существования T. с. подтверждена лишь прямыми вариационными методами (Ю. С. Тюпкин, В. А. Фатеев, А. С. Шварц, 1976) и численными расчётами. Помимо монопольных решений модель допускает т. н. д и о н ы Джулиа - Зи (В. Julia, A. Zee, 1975), т. <е. объекты с электрическим и магнитным зарядами. Физически монополи предсказываются теорией Великого объединения и могут выступать в роли катализатора распада протона - эффект Каллана - Рубакова (В. А. Рубаков, 1981; С. G. Callan, 1982), но до сих пор не обнаружены экспериментально.
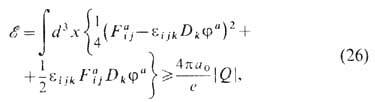
Другими известными примерами T. с. в (3 + 1) измерениях являются инстантоны и скирмионы. И н с т а н т о н ы обнаружены (А. А. Белавин, A. M. Поляков, Тюпкин, Шварц, 1975) как частицеподобные решения в евклидовом, чисто калибровочном варианте лагранжиана предыдущей модели, т. <е. когда в отсутствие полей Хиггса, Янга- Миллса поля Am. рассматриваются в мнимом времени. Пространство-время Минковского при замене
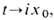 где x0 - вещественная переменная, эквивалентно евклидову 4-мерному пространству. Термин "инстантон" (от англ. instant - мгновенный, немедленный; момент) предложен т'Хоофтом для обозначения T. с., к-рые, в отличие от вышеописанных солитонов, локализованы не только в пространстве, но и во времени. В силу своих особых свойств инстантоны могут осуществлять мгновенные переходы между полями с разной топологией, что имеет существенное значение в процессах перестройки вакуумов в квантовой хромодинамике и других калибровочных теориях.
где x0 - вещественная переменная, эквивалентно евклидову 4-мерному пространству. Термин "инстантон" (от англ. instant - мгновенный, немедленный; момент) предложен т'Хоофтом для обозначения T. с., к-рые, в отличие от вышеописанных солитонов, локализованы не только в пространстве, но и во времени. В силу своих особых свойств инстантоны могут осуществлять мгновенные переходы между полями с разной топологией, что имеет существенное значение в процессах перестройки вакуумов в квантовой хромодинамике и других калибровочных теориях.
С к и р м и о н ы - T. с. нелинейной сигма-модели со спонтанно нарушенной киральной симметрией, предложенной T. X. P. Скирмом (T. H. R. Skyrme, 1961; см. Скирма модель). Изначально скирмионы предназначались для описания барионов как протяжённых локализованных структур с нетривиальным топологич. зарядом Q (типа степени отображения
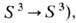 к-рый интерпретировался как бари онное число. При этом модель Скирма оказалась достаточно удачным и простым прообразом эффективной мезонной
к-рый интерпретировался как бари онное число. При этом модель Скирма оказалась достаточно удачным и простым прообразом эффективной мезонной
теории (пока неизвестной и труднодоступной), к к-рой должна сводиться теория сильных взаимодействий (квантовая хромодинамика) в низкоэнергетич. секторе. В рамках этой достаточно простой модели удаётся удовлетворительным образом описывать как спектроскопию основных состояний адронов, так и их взаимодействия. Позже выяснилось, что на основе модели Скирма и её модификаций, таких, как модель Скирма - Мантона (N. S. Manton, 1987), можно получать разумные ответы как в высокоэнергетич. физике адронов, так и при описании плотной ядерной материи. В частности, можно получить оценку для плотности энергии ядерной материи
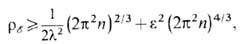
где
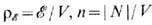 - плотность числа частиц, V- объём, занимаемый материей, l, e-параметры модели.
- плотность числа частиц, V- объём, занимаемый материей, l, e-параметры модели.
Оценка хорошо согласуется с выводами теории кварк-глю-онной плазмы. Другим предсказанием модели является то, что по мере уплотнения системы изолированных скирми-онов они вначале образуют гранецентрир. кубич. решётку с нек-рой постоянной a', затем скирмионы начинают расширяться, теряют свою индивидуальность, и при дальнейшем уплотнении происходит фазовый переход системы в конденсированное состояние. При этом имеет место эффект уменьшения энергии (массы), приходящейся на один скирмион, достигающий предельного значения при нек-ром a'=a'0 [9], [10].
Одной из наиб. привлекательных особенностей модели Скирма является реализованный в её рамках механизм построения фермионных состояний (нуклонов) из бозон-ных полей (мезонов), т. <н. явление Ф е р м и - Б о з е т р а н с м у т а ц и и. В связи с этим термин "скирмион" (предложен В. И. Санюком, 1981) приобрёл расширенный смысл - так называются теперь любые T. с., возникающие как частицеподобные решения в чисто бозонных теориях поля, но подчиняющиеся статистике Ферми - Дирака после квантования, т. е. характеризующиеся полуцелым спином. Более того, развитие этой идеи показало, что возможны T. с. с произвольным дробным значением спина, подчиняющиеся т. н. промежуточным статистикам (см. Парастатистика). Такие T. с. известны также под назв. а н и о н ы (от англ. any - всякий, любой). Термин предложен Ф. Вилчеком (F. Wilczek, 1982) и отражает факт допустимости практически любого дробнозначного спина у таких частиц, к-рые используются в моделях высокотемпературной сверхпроводимости (см. Оксидные высокотемпературные сверхпроводники). В теории квантового Холла эффекта также рассматриваются T. с. с дробным спином под назв. "холлоны", в гравитации - "геоны" и т. д.
T. с. с д р о б н ы м с п и н о м. Проиллюстрируем появление Т. <е. с дробным спином на примере (2+1)-мерной нелинейной s-модели, обсуждавшейся ранее в связи с вихрями Белавина - Полякова [ур-ния (12), (13)] Топологич. заряд модели (15) можно представить как
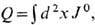 где J0 - временная компонента сохраняющегося независимо от динамики модели топологич. тока
где J0 - временная компонента сохраняющегося независимо от динамики модели топологич. тока
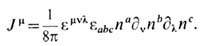 (27)
(27)
Закон сохранения
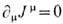 позволяет переписать ток (27) в виде ротора от нек-рого вспомогательного калибровочного поля Am:
позволяет переписать ток (27) в виде ротора от нек-рого вспомогательного калибровочного поля Am:

Далее, вместо (13) можно записать лагранжиан
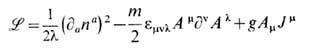
(g- нек-рая константа взаимодействия), из к-рого соотношение (28) получается как ур-ние Эйлера - Лагранжа в отношении Am, если считать данное поле независимым. В подходящей калибровке (напр., д iAi=0) интегрирование по вспомогательному (не динамическому) полю Am приводит к эфф. действию
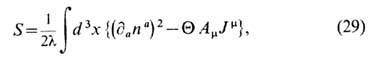
где
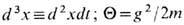 -вещественный параметр, возникающий в (29) как коэф. при топологич. члене, в к-ром легко узнать индекс Хопфа (20), переписанный в виде
-вещественный параметр, возникающий в (29) как коэф. при топологич. члене, в к-ром легко узнать индекс Хопфа (20), переписанный в виде 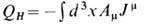 Действия вида (29) известны в калибровочных теориях (в частности, в квантовой хромодинамике) под назв. "Q-действие ". Его происхождение связано с локальной калибровочной инвариантностью гамильтонианов в таких теориях, вследствие чего собств. ф-ции для заданного значения энергии определяются с точностью до постоянного сдвига фазы. Соответственно гильбертово пространство теории разбивается на секторы, нумеруемые непрерывным параметром Q, и в каждом из них есть своё вакуумное состояние ( "Q-вакуум ") и построенные над ним "Q -миры ". Эти "Q-миры " не сообщаются друг с другом в силу суперотбора правил, однако связь между ними возможна за счёт инстантонного туннелирования (подробно см, в [1]).
Действия вида (29) известны в калибровочных теориях (в частности, в квантовой хромодинамике) под назв. "Q-действие ". Его происхождение связано с локальной калибровочной инвариантностью гамильтонианов в таких теориях, вследствие чего собств. ф-ции для заданного значения энергии определяются с точностью до постоянного сдвига фазы. Соответственно гильбертово пространство теории разбивается на секторы, нумеруемые непрерывным параметром Q, и в каждом из них есть своё вакуумное состояние ( "Q-вакуум ") и построенные над ним "Q -миры ". Эти "Q-миры " не сообщаются друг с другом в силу суперотбора правил, однако связь между ними возможна за счёт инстантонного туннелирования (подробно см, в [1]).
Формально топология, член в (29) аналогичен члену Черна (Чжэня)- Саймонса (S. S. Chern, J. Simons, 1971) в топологических квантовых теориях поля, и именно его присутствие обеспечивает наличие дробнозяачного полного утл. момента (и, соответственно, спина) в моделях такого рода. При нечётном числе измерений пространства-времени d можно задать т. н. д е й с т в и е Ч е р н а - С а йм о н с а SCS как интеграл от d -формы по d -мерному пространственно-временному многообразию
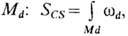 так что SCS не зависит от пространственно-временной метрики и является инвариантом в отношении диффеоморфизмов многообразия М d . В простейшем нетривиальном случае d=3 = 2+1 и 3-форма w3 (см. Дифференциальная форма )выражается через 1-формы связности
так что SCS не зависит от пространственно-временной метрики и является инвариантом в отношении диффеоморфизмов многообразия М d . В простейшем нетривиальном случае d=3 = 2+1 и 3-форма w3 (см. Дифференциальная форма )выражается через 1-формы связности 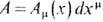 в виде
в виде
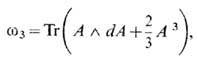
что даёт для действия Черна - Саймонса выражение (с подходящим нормировочным коэф.)
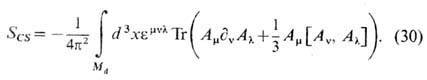
В силу соотношений (27) и (28) ясно, что (30) можно переписать через компоненты n -поля в нек-рой фиксированной калибровке и понимать индекс Хопфа в действии (29) как член, описывающий эфф. дальнодействие между фундаментальными n -полями. Используя действие Черна- Саймонса типа (29), удаётся получить описание аномалий в калибровочных теориях, в частности в квантовой хромодинамике [11]. Рассматривая стандартное действие для полей Янга - Миллса с добавленным членом Черна - Саймонса, описывают массивные векторные бозоны - "топологические массивные калибровочные теории" с "топологической массой", индуцируемой SCS. Если действие для полевой теории выбирается просто в виде действия Черна - Саймонса типа (30), то такие свободные от метрики теории, получившие назв. "топологические теории поля", оказываются точно решаемыми, обладают более широкими группами симметрии и по этой причине активно используются в совр. теориях струн (см. Струн теория), суперструн, супергравитации, в конформных теориях поля, втеории узлов и т. д. [12].
Вернёмся к идее экзотических спинов и статистик, где определяющую роль играет наличие в действии (29) члена Черна - Саймонса (30). Будем адиабатически поворачивать T. с. на угол 2p за период времени T. В результате такого поворота волновая ф-ция приобретает множитель exp(iS), где S- соответствующее классич. действие. Полный угл. момент T. с. J определяется соотношением
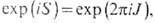 и для стандартного действия s-модели [первый член в ф-ле (29), имеющий порядок
и для стандартного действия s-модели [первый член в ф-ле (29), имеющий порядок 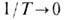 при
при 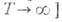 получаем J= 0. Простые выкладки показывают, что для действия (2+1)-мерного T. с. в виде (29) полный угл. момент
получаем J= 0. Простые выкладки показывают, что для действия (2+1)-мерного T. с. в виде (29) полный угл. момент
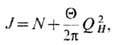
где QH -индекс Хопфа,
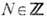 - целочисленное значение стандартного орбитального угл. момента, в то время как второй член свидетельствует о том, что спин T. с. принимает дробные значения. Значение Q определяется, как правило, из феноменологич. соображений, индекс Хопфа принимает только целочисленные значения, поэтому при Q/p=2N спин T. с. будет целым, при Q/p=2N+1-полуцелым, во всех др. случаях - дробнозначным.
- целочисленное значение стандартного орбитального угл. момента, в то время как второй член свидетельствует о том, что спин T. с. принимает дробные значения. Значение Q определяется, как правило, из феноменологич. соображений, индекс Хопфа принимает только целочисленные значения, поэтому при Q/p=2N спин T. с. будет целым, при Q/p=2N+1-полуцелым, во всех др. случаях - дробнозначным.
Лит.:1) Раджараман Р., Солитоны и инстантоны в квантовой теории поля, пер. с англ., M., 1985; 2) Шварц А. С., Квантовая теория поля и топология, M., 1989; 3) Воловик Г. E., Минеев В. П., Физика и топология, M., 1980; 4) Косевич A. M., Иванов Б. А., Ковалев А. С., Нелинейные волны намагниченности. Динамические и топологические солитоны, К., 1983; 5) Додд Р. и др., Солитоны и нелинейные волновые уравнения, пер. с англ., M., 1988; 6) Makhankov V. G., Soliton phenomenology, Dordrecht-[а. о.], 1990; 7) Райдер Л., Квантовая теория поля, пер. с англ., M., 1987; 8) Рыбаков К). П., Устойчивость многомерных солитонов в киральных моделях и гравитации, в кн.: Итоги науки и техники, сер. Классическая теория поля и теория гравитации, т. 2, M., 1991; 9) Маханьков В. Г., Рыбаков Ю. П., Санюк В. И., Модель Скирма и сильные взаимодействия, "УФН", 1992, т. 162, № 2, с. 1; 10) Makhankov V. G., Rybakov Y. P., Sanyuk V. L, The Skyrme model. Fundamentals, methods, applications, B.- L., 1993; 11) Морозов А. Ю., Аномалии в калибровочных теориях, "УФН", 1986, т. 150, в. 3, с. 337; 12) Balachandran A. P. et al.. Classical topology and quantum states, Singapoore, 1991. В. И. Санюк.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
