- СЖАТОЕ СОСТОЯНИЕ
- СЖАТОЕ СОСТОЯНИЕ
-
электромагнитного поля - состояние поля, прик-ром дисперсии флуктуации канонически сопряжённых компонент поля не равны. <Возможны классич. и квантовые С. с. В первом случае оказываются неравнымидисперсии квадратур классич. флуктуации (см. [1], с. 125); для квантовогоС. с. дисперсия любой одной канонически сопряжённой компоненты меньше дисперсиив когерентном состоянии. Понятие С. с. возникло в процессе изучения (1960-70-егг.) статистич. характеристик излучения (долазерные эксперименты по корреляцияминтенсивности), детального исследования необычных свойств лазерного света. <Различают С. с. квадратурносжатые и состояния с подавленными флуктуациямичисла фотонов или фазы.
Для когерентного состояния поля характерно пуассоновское распределениефотонов
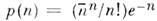 сдисперсией
сдисперсией 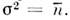 В поле с меньшей дисперсией флуктуации подавлены квантовые флуктуации интенсивности, статистика фотоотсчётов сглажена во времени. В этом случае распределениефотонов более узкое, чем пуассоновское, и такое поле наз. с у б п у а сс о н о в с к и м. Уровень шума детектирования излучения с субпуассоновскойстатистикой фотонов оказывается ниже уровня дробового шума. Поэтомуиспользование эл.-магн. полей с субпуассоновской статистикой представляетинтерес для высокочувствит. и высокоточных измерений, в оптич. связи испектроскопии.
В поле с меньшей дисперсией флуктуации подавлены квантовые флуктуации интенсивности, статистика фотоотсчётов сглажена во времени. В этом случае распределениефотонов более узкое, чем пуассоновское, и такое поле наз. с у б п у а сс о н о в с к и м. Уровень шума детектирования излучения с субпуассоновскойстатистикой фотонов оказывается ниже уровня дробового шума. Поэтомуиспользование эл.-магн. полей с субпуассоновской статистикой представляетинтерес для высокочувствит. и высокоточных измерений, в оптич. связи испектроскопии.Схематичное представление С. с. на фазовой плоскости дано на рис. 1.Векторами обозначены ср. амплитуды, пунктиром - область неопределённости когеренткого состояния, эллипсами - области неопределённостиС. с. При соответствующей ориентации эллипса сжатия относительно регулярнойсоставляющей поля возможно подавление как амплитудных (рис. 1,б), так ифазовых (рис. 1,в) флуктуации.
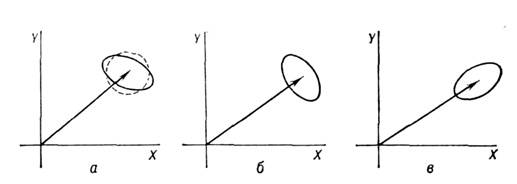
Рис. 1. Схематичное представление сжатых состояний электромагнитногополя на фазовой плоскости: а - произвольная ориентация эллипса сжатия;б - подавлены амплитудные флуктуации; в - подавлены фазовые флуктуации.
В квантовой оптике напряжённость одномодового электрич. поляописывается оператором
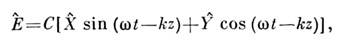
где
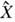 и
и 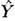 - операторыквадратур:
- операторыквадратур: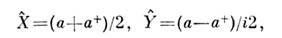
w - частота, k - волновое число, z -направление распространенияизлучения, С= const, а и а + - операторыуничтожения и рождения фотона. Операторы квадратур удовлетворяют коммутац. <соотношению
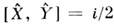 , а их дисперсии
, а их дисперсии 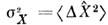 ,
,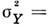
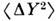 - соотношению неопределённостей
- соотношению неопределённостей 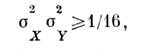
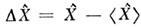 ,
,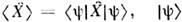 - вектор состояния поля,
- вектор состояния поля,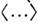 - квантовомеханич. усреднение. В когерентном и вакуумном состояниях
- квантовомеханич. усреднение. В когерентном и вакуумном состояниях 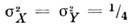 В квантовом С. с. флуктуации одной из квадратур, напр.,
В квантовом С. с. флуктуации одной из квадратур, напр.,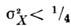 ,тогда как
,тогда как 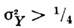 или наоборот.
или наоборот.В случае классич. флуктуации операторы а, а + заменяютсякомплексными амплитудами А, А*, при этом квадратуры
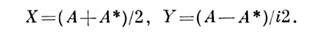
При классич. сжатии
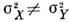
Поля в С. с. являются периодически нестационарными [1], в чём легкоубедиться, используя классич. описание. Полагая квадратуры некоррелированными, <для ср. интенсивности поля имеем:
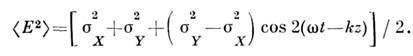
Методы получения сжатых состояний основываются на нелинейных радиофиз. <и оптич. процессах. В оптике С. с. могут возникать в трёх- и четырёхчастотныхпараметрич. взаимодействиях (см. Взаимодействие световых волн), пригенерации высших гармоник, в эффектах самовоздействия, комбинац. рассеянии, <многофотонных процессах и т. п. Возможно также непосредств. создание высокостабильныхлазерных источников излучения, в к-рых подавление квантовых флуктуацииосуществляется либо депрессией шумов накачки, либо введением отрицат. обратнойсвязи.
Преобразование вакуумного или когерентного состояния, к-рому соответствуютоператоры а и а +, в сжатое (соответственно операторыbи b+ )описывается операторным ур-нием в представлении Гейзенберга:
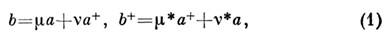
где
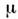 и v - постоянные, удовлетворяющие соотношению
и v - постоянные, удовлетворяющие соотношению 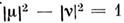 . Тогда дисперсии флуктуации квадратурных компонент
. Тогда дисперсии флуктуации квадратурных компонент 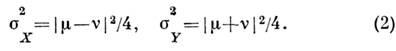
Преобразование вакуумного состояния в сжатое иначе можно записать как[2]:
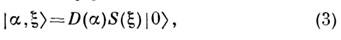
где
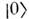 - вектор вакуумного состояния, а
- вектор вакуумного состояния, а 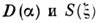 - операторы смещения и сжатия:
- операторы смещения и сжатия: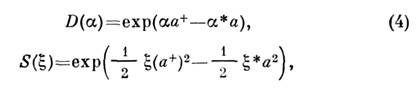
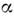 и
и 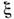 - в общем случае комплексные числа.
- в общем случае комплексные числа.Состояние
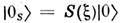 принято называть вакуумным С. с. (
принято называть вакуумным С. с. (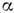 = 0).
= 0).С. с. возникает, напр., при вырожденном параметрич. взаимодействии. <В поле интенсивной классич. накачки параметрич. усиление слабого сигналаописывается ур-нием для операторов в представлении Гейзенберга:

где
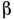 - комплексный коэф., зависящий от нелинейных свойств среды и амплитудынакачки. Решение (5) имеет вид:
- комплексный коэф., зависящий от нелинейных свойств среды и амплитудынакачки. Решение (5) имеет вид: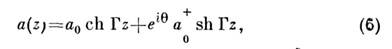
где
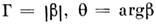 , а операторы а 0 и
, а операторы а 0 и 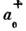 - параметры на входе нелинейной среды.
- параметры на входе нелинейной среды.Операторы квадратур преобразуются следующим образом:
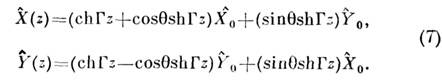
Аналогичные соотношения получаются и при полностью классическом описаниипараметрич. усиления (с заменой операторов комплексными амплитудами). Согласно(7), дисперсии квадратур при
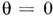
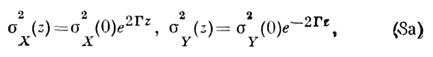
а при
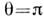
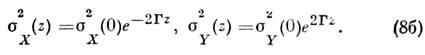
Поведение квадратур, т. о., существенно зависит от фазы накачки
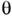 .Фазовая селективность рассматриваемого параметрич. процесса - важнейшаяего особенность, исследованная в радиодиапазоне в нач. 1960-х гг. [4].Тогда же были продемонстрированы возможности управления статистич. характеристикамиэл.-магн. полей, снижения уровня фазовых флуктуации, улучшения характеристиксистем выделения сигнала из шума. Действительно, при соответствующей ориентацииэллипса сжатия на фазовой плоскости, регулируемой выбором фазы накачки, <подавление флуктуации квадратуры приводит к снижению фазовых флуктуации. <Это просто показать на примере клаcсич. С. с. Пусть напряжённость поля(эллипс ориентирован вдоль оси X)
.Фазовая селективность рассматриваемого параметрич. процесса - важнейшаяего особенность, исследованная в радиодиапазоне в нач. 1960-х гг. [4].Тогда же были продемонстрированы возможности управления статистич. характеристикамиэл.-магн. полей, снижения уровня фазовых флуктуации, улучшения характеристиксистем выделения сигнала из шума. Действительно, при соответствующей ориентацииэллипса сжатия на фазовой плоскости, регулируемой выбором фазы накачки, <подавление флуктуации квадратуры приводит к снижению фазовых флуктуации. <Это просто показать на примере клаcсич. С. с. Пусть напряжённость поля(эллипс ориентирован вдоль оси X)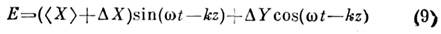
или
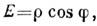
где
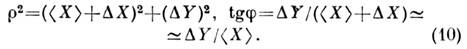
Флуктуации фазы
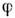 связаны с флуктуациями квадратуры Y. Подавление флуктуации
связаны с флуктуациями квадратуры Y. Подавление флуктуации 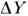 приводит к изменению функции распределения фазы
приводит к изменению функции распределения фазы 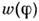 . В связи с этим осн. метод исследования С. с. в радиодиапазоне состоитв измерении распределения
. В связи с этим осн. метод исследования С. с. в радиодиапазоне состоитв измерении распределения 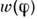 [4].
[4].К возникновению С. с. приводит также эффект с а м о в о з д е и с тв и я. При распространении излучения в среде с кубичной нелинейностью появляетсяфазовая добавка, пропорц. числу фотонов
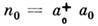 (эффект фазовой самомодуляции света). Для одномодового излученияэтот эффект описывается ур-нием
(эффект фазовой самомодуляции света). Для одномодового излученияэтот эффект описывается ур-нием 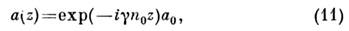
где коэф.
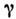 определяется кубичной нелинейностью среды. В случае исходного когерентногосостояния
определяется кубичной нелинейностью среды. В случае исходного когерентногосостояния 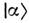 с амплитудой
с амплитудой 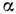 ,где
,где 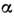 - собств. значение оператора
- собств. значение оператора 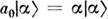 , и оптим. фазы сигнала
, и оптим. фазы сигнала 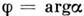 , удовлетворяющей соотношению
, удовлетворяющей соотношению 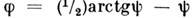 ,
,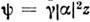 , минимальная дисперсия квадратуры
, минимальная дисперсия квадратуры 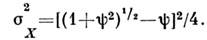
При этом дисперсия второй квадратуры максимальна:
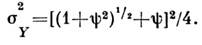
При нелинейном оптич. преобразовании (11) статистика фотонов не меняется:
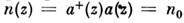 . Однако интерференция поля, находящегося в когерентном состоянии, с полем, <преобразованным согласно (11), позволяет получить излучение с субпуассоновскойстатистикой [4].
. Однако интерференция поля, находящегося в когерентном состоянии, с полем, <преобразованным согласно (11), позволяет получить излучение с субпуассоновскойстатистикой [4].Для регистрации С. с. оптич. излучения обычно используется балансноегомодинное детектирование (рис. 2). Сжатый свет, к-рому соответствуют операторы
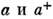 , смешивается с мощным когерентным излучением гетеродина (операторы
, смешивается с мощным когерентным излучением гетеродина (операторы 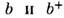 ). Операторы уничтожения, описывающие излучение в каждом из каналов (индексы«1» и «2») после смешения, имеют вид:
). Операторы уничтожения, описывающие излучение в каждом из каналов (индексы«1» и «2») после смешения, имеют вид: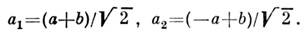
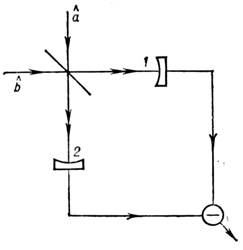
Рис. 2. Схема балансного гомодинного фотодетектирования: 1 и 2 -фотоприёмники в каналах.
Для фотоприёмников с единичным квантовым выходом оператор разностногофототока равен
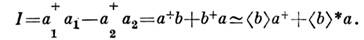
Приближённая часть выражения соответствует излучению гетеродина в случае, <когда его можно описывать классически:
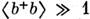 . Подбором фазы гетеродина
. Подбором фазы гетеродина 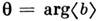 можно добиться того, чтобы разностный фототок определялся лишь одной изквадратур регистрируемого поля, напр.
можно добиться того, чтобы разностный фототок определялся лишь одной изквадратур регистрируемого поля, напр.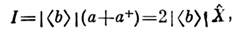
а его дисперсия - дисперсией этой квадратуры:
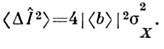
Если на входе гетеродина излучение в С. с. отсутствует, то дисперсияопределяется вакуумными флуктуациями
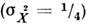 и уровень дробового шума описывается ф-лой Шоттки. При подаче на смесительизлучения в С. с. уменьшается дробовой шум детектирования. Др. способ исследованияС. с. базируется на регистрации усиленной квадратуры компоненты. При сильномсжатии классич. и многомодовые квантовые С. с. обладают фазосопряжённымспектром, т. е. фазы фурье-компонент поля, расположенных симметрично относительноср. частоты, комплексно сопряжены (равны по абс. величине, но имеют разныезнаки). Это свойство приводит к тому, что при удвоении частоты широкополосногоспектра С. с. в спектре второй гармоники формируется очень узкий пик [4].Квантовая трактовка этого явления - смешение коррелиров. пар фотонов, рождаемыхпри параметрической люминесценции.
и уровень дробового шума описывается ф-лой Шоттки. При подаче на смесительизлучения в С. с. уменьшается дробовой шум детектирования. Др. способ исследованияС. с. базируется на регистрации усиленной квадратуры компоненты. При сильномсжатии классич. и многомодовые квантовые С. с. обладают фазосопряжённымспектром, т. е. фазы фурье-компонент поля, расположенных симметрично относительноср. частоты, комплексно сопряжены (равны по абс. величине, но имеют разныезнаки). Это свойство приводит к тому, что при удвоении частоты широкополосногоспектра С. с. в спектре второй гармоники формируется очень узкий пик [4].Квантовая трактовка этого явления - смешение коррелиров. пар фотонов, рождаемыхпри параметрической люминесценции.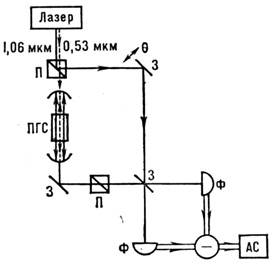
Рис. 3. Схема эксперимента по генерации сжатых состояний: задающийлазер генерирует излучение на длине волны
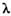 = 1,06 мкм (сплошные линии) и на
= 1,06 мкм (сплошные линии) и на 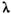 = 0,53мкм (штриховая линия); перемещением одного из плоских зеркал вноситсяфазовая задержка
= 0,53мкм (штриховая линия); перемещением одного из плоских зеркал вноситсяфазовая задержка 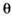 ;П - поляризатор; 3 - зеркало; Ф - фотодиод; АС - анализатор спектра; ПГС- параметрический генератор света.
;П - поляризатор; 3 - зеркало; Ф - фотодиод; АС - анализатор спектра; ПГС- параметрический генератор света.Ярким подтверждением существования квантовых С. с. явился эксперимент[5], схема к-рого приведена на рис. 3. Здесь реализовано коллинеарное трёхфотонноепараметрич. взаимодействие в оптич. резонаторе в допороговом режиме. Излучениенакачки (
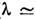 0,53 мкм), представляющее собой вторую гармонику задающего лазера на гранатес неодимом, поступает в резонатор, где генерируется С. с. на
0,53 мкм), представляющее собой вторую гармонику задающего лазера на гранатес неодимом, поступает в резонатор, где генерируется С. с. на 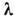 = 1,06 мкм. Одноврем. излучение задающего лазера с
= 1,06 мкм. Одноврем. излучение задающего лазера с 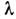 =1,06 мкм отщепляется от осн. пучка и смешивается с излучением в С. с. <в схеме балансного гомодинного детектирования. Осн. результат эксперимента, <заключающийся в появлении провалов под уровнем дробового шума, представленна рис. 4, где изображена зависимость напряжения шума фототока от фазыгетеродина. Глубина провалов составляет прибл. 50%.
=1,06 мкм отщепляется от осн. пучка и смешивается с излучением в С. с. <в схеме балансного гомодинного детектирования. Осн. результат эксперимента, <заключающийся в появлении провалов под уровнем дробового шума, представленна рис. 4, где изображена зависимость напряжения шума фототока от фазыгетеродина. Глубина провалов составляет прибл. 50%.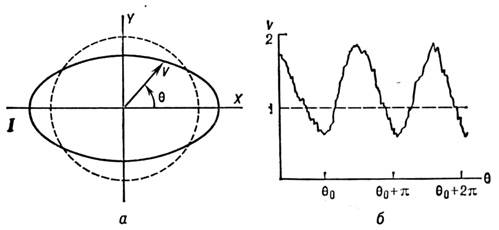
Рис. 4. Зависимость напряжения шумов разностного фототока от фазыгетеродина: а - область квантовой неопределённости; б - результат эксперимента. <Пунктирными линиями показан уровень дробового шума и соответствующее емувакуумное состояние (его область квантовой неопределённости).
Осн. причинами, препятствующими достижению глубокого сжатия, кроме техн. <шумов являются любые потери излучения (в т. ч. и вследствие неединичного квантового выхода фотоприёмников), а также многомодовость реальныхсветовых пучков, ограниченных как в пространстве, так и во времени. Деструктивнаяроль потерь объясняется их вероятностным характером: из пучка с нек-ройвероятностью осуществляется изъятие априорно неизвестных фотонов, и ихпоток, первоначально определённым образом упорядоченный, приобретает случайныйхарактер, что и снижает глубину сжатия, В многомодовом излучении каждаямода может быть «сжата» по-своему, т. е. иметь разл. эффективность и ориентациюэллипса сжатия на фазовой плоскости. Поскольку при регистрации происходитаддитивное сложение мод, в результирующей картине возникает «размазывание»сжатия. Тем не менее возможно появление С. с. в сверхкоротких импульсах, <спектр сжатия к-рых широкополосный. Это выгодно отличается от генерацииС. с. в резонаторах, где сжатие проявляется лишь до диапазона МГц.
Эфф. формирование импульсов сжатого света возможно в процессе параметрич. <усиления в поле импульсной накачки [6], а также в оптич. солитонах за счётфазовой самомодуляции [4], необходимой для их формирования.
С. с. эл.-магн. поля достигается также подавлением квантовых флуктуациив лазерах, при этом, как правило, генерируется свет с субпуассоновскойстатистикой фотонов, являющийся частным случаем С. с. Между интенсивностьюгенерируемого излучения и накачкой устанавливают отрицат. обратную связь. <Здесь необходимо применение методов квантовых невозмущающих измерений интенсивности, <чтобы не разрушить актом измерения субпуассоновского состояния. Возможны, <напр., два варианта реализации таких измерений. Первый предполагает использованиесреды с кубичной нелинейностью, в к-рой при распространении генерируемогоизлучения осуществляется фазовая самомодуляция. Возникающий нелинейныйфазовый набег регистрируется при прохождении той же среды слабым пробнымпучком с последующим его гетеродинированием. В результате фазовая модуляцияпробного пучка переходит в амплитудную, к-рая и используется в линии отрицат. <обратной связи лазерной накачки. Второй вариант заключается в управлениинакачкой невырожденного параметрич. генератора. При этом используется жёсткаявзаимная корреляция фотонов в сигнальной и холостой волнах: они рождаютсятолько одновременно. Фототок детектора, регистрирующего холостую волну, <поступает в линию отрицат. обратной связи, регулирующей мощность накачки, <тем самым стабилизируя амплитуду сигнальной волны. Последнее и приводитк возникновению в ней субпуассоновской статистики фотонов.
Генерировать субпуассоновский свет можно также стабилизируя квантовыефлуктуации тока накачки полупроводникового лазера. Достичь субпуассоновскойстатистики электрич. сигнала (электронов) сравнительно несложно, напр. <с помощью эффекта Кулона в электронно-лучевой трубке. При высокой эффективностипреобразования заряж. частиц тока накачки в испускаемые фотоны (неединичнаяэффективность эквивалентна потерям) субпуассоновское состояние накачкипереходит в генерируемый свет, т. е. из радиодиапазона в оптический. Можноиспользовать и обратный фотоэффект Франка - Герца, однако эффективностьпреобразования при этом оказывается ниже.
Подавление шума, связанного с созданием инверсной населённости в лазере, <достигается также применением мощной импульсной периодич. накачки, к-раяпереводит все электроны на верх. уровень рабочего перехода. При этом такжесоздаются необходимые предпосылки для генерации субпуассоновского света.
До сих пор обсуждалось формирование С. с. эл.-магн. поля во времени. <В общем случае можно говорить о пространственно-временном сжатии [4, 7],характеризующем области пространственных и временных частот, в к-рых квантовыефлуктуации подавлены. Наглядным является пример пространственного сжатияпри вырожденном параметрич. усилении когерентных волн с неколлинеарнойгеометрией взаимодействия. Сжатие в сигнальной и холостой волнах в отдельностиотсутствует, но оно возникает при их интерференции с разностью фаз, кратной
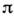 .В частности, макс. сжатие проявляется в интерференц. максимумах. Числоинтерференц. полос на единицу длины определяет пространственную частотусжатия. При параметрич. взаимодействии пучков с конечной апертурой пространственныйспектр сжатия, очевидно, более сложный.
.В частности, макс. сжатие проявляется в интерференц. максимумах. Числоинтерференц. полос на единицу длины определяет пространственную частотусжатия. При параметрич. взаимодействии пучков с конечной апертурой пространственныйспектр сжатия, очевидно, более сложный.Лит.:1) А х м а н о в С. А., Дьяков Ю. Е., Ч и р к и н А. С.,Введение в статистическую радиофизику и оптику, М., 1981; 2) Смирнов Д. <Ф., Т р о ш и н А. С., Новые явления в квантовой оптике, «УФН», 1987, т.153, с. 233; 3) К л ы ш к о Д. Н., Фотоны и нелинейная оптика, М., 1980;4) Ахманов С. А., Велинский А. В., Ч и р к и н А. С., Фазовая биетабильностьи мультистабильность в сосредоточенных и распределенных системах: классическийи квантовый аспекты, в кн.: Новые физические принципы оптической обработкиинформации, под ред. С. А. Ахманова, М. А. Воронцова, М., 1990; 5) W uL. и др., Generation of squeezed states by parametric down conversion,«Phys. Rev. Lett.», 1986, y. 57, p. 2520; 6) S1usher R. Е. и др., Pulsedsqueezed light, «Phys. Rev. Lett.», 1987, v. 59, p. 2566; 7) К о л о бо в М. И., С о к о л о в И. В., Поведение сжатых состояний света в пространствеи квантовые шумы оптических изображений, «ЖЭТФ», 1989, т. 96, с. 1945;Килин С. Я., Квантовая оптика. Поля и их детектирование, Минск, 1990; 8)Б ы к о в В. П., Основные особенности сжатого света, «УФН», 1991, т. 161,№ 10, с. 145; 9) Т а и ш М. К., Салэ Б. Э. А., Сжатые состояния света,«УФН», 1991, т. 161, Ni4, с. 101. А. В. Белинский, А. С. Чиркин.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
