- ПОЛОСТЬ РОША
- ПОЛОСТЬ РОША
-
- пространственная область определяющая макс. размеры стационарной вращающейся звезды (одиночной или в двойной системе). Границей П. <Р. <является т. н. критич. эквипотенциальная поверхность, на к-рой эфф. сила притяжения (см. ниже) обращается в нуль (хотя бы в одной точке). П. P. названа по имени Э. А. Роша (Е. A. Roche), исследовавшего фигуры равновесия тел вращения (1849-51) Большое значение понятие П. Р. приобрело во 2-й пол. 20 в. в связи с задачами экваториального истечения из быстровращающихся одиночных звёзд, а также перетекания вещества с одной компоненты на другую в тесных двойных звёздах на поздних стадиях их эволюции Поверхность стационарной вращающейся звезды совпадает с нек-рой эквипотенциальной поверхностью Эфф. потенциал F на поверхности одиночной вращающейся звезды определяется суммой гравитац. Ф г и центробежного Ф ц потенциалов. Вращение нарушает сферически-симметричное распределение массы в звезде однако для большинства обычных звёзд из-за сильной концентрации вещества к центру обусловленные вращением отличия гравитац. потенциала от сферически-симметричного малы. Поэтому Ф г на поверхности таких звезд мало отличается от потенциала точечной мас-сы:
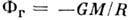( М - масса звезды, R - расстояние от центра звезды). При вращении о нек-рой угл. скоростью 
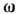(не зависящей от координат) центробежный потенциал Ф ц=-(1/2)w2R2sin2q (q-полярный угол). Т. о., форма стационарной вращающейся звезды (рис. 1) определяется одной из эквипотенциальных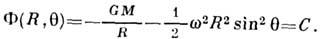 
Рис. 1. Вид сечений эквипотенциальных поверхностей одиночной вращающейся звезды плоскостью, проходящей через ось вращения. Критическая эквипотенциаль выделена полужирной линией, О- центр масс звёзд.
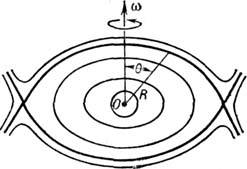
На экваторе критич. эквипотенциальной поверхности
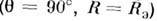сила притяжения на единицу массы, равная 
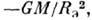уравновешена центробежной силой 
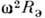(т. е. эфф. сила притяжения 
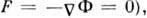и постоянная 
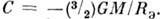На полюсе 
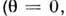R =
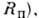где центробежная сила отсутствует,
=
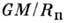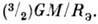Максимально возможное отношение экваториального 
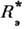и полярного 
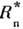радиусов звезды, заполняющей П. Р., 
= 
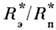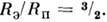С уменьшением размеров звезды (относительно П. Р.) 
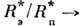1. Угл. скорость вращения стационарной звезды не может превышать величины 
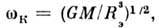иначе у неё начнётся экваториальное истечение вещества. Однако не все звёзды могут быть ускорены к.-л. из известных механизмов до 
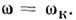Так, в рамках моделей нейтронных звёзд со слабой концентрацией массы к центру (с "жёстким" ур-нием состояния) устойчивость звезды нарушается при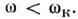 
Понятие эквипотенциальных поверхностей и П. Р. можно ввести также и для системы двух звёзд, обращающихся вокруг общего центра тяжести по круговым орбитам с пост. угл. скоростью
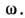В неинерциальной системе координат, вращающейся с той же угл. скоростью, эфф. потенциал стационарен и определяется суммой гравитац. потенциалов обеих компонент и центробежного потенциала: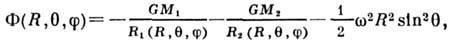
где
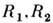и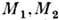 
- расстояния от центров и массы звёзд,
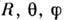- сферич. координаты (центр системы - в центре масс, ось 
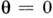параллельна 
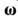), предполагается синхронность вращения (угл. скорость вращения звёзд равна 
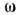).Рис. 2. Вид сечений эквипотенциальных поверхностей в двойной звёздной системе плоскостью, проходящей через центры масс компонент и ортогональной оси вращения системы. Критическая эквипотенциаль выделена полужирной линией,
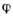- азимутальный угол, О - центр масс системы. Внешние эквипотенциали, соответствующие С =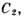
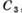не показаны.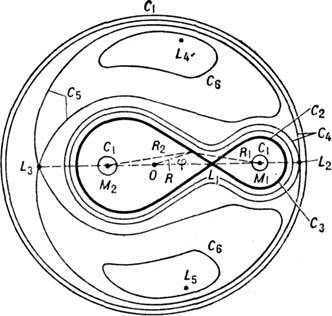
Эквипотенциальные поверхности,
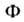= С, при больших значениях модуля 
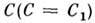состоят из окружающих каждую массу почти концентрич. сфер и одной внеш. поверхности, по форме близкой к круговому цилиндру (рис. 2). С уменьшением 
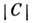размеры эквипотенциальных поверхностей возрастают, они деформируются, превращаясь в вытянутые навстречу друг другу фигуры, и при нек-ром значении 
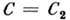имеет место пересечение этих фигур. Точка пересечения 
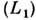наз. внутр. либрац. точкой Лагранжа. Эквипотенциальная поверхность, проходящая через 
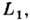наз. критической и определяет П. Р. каждой из компонент двойной системы. Поверхности звёзд должны совпадать с одной из внутр. эквипотенциалей. При заполнении одной из компонент своей П. Р. начинается интенсивное перетекание вещества на соседнюю компоненту.В зависимости от соотношения между размерами компонент и П. Р. существует классификация двойных звёздных систем: разделённые системы, у к-рых обе компоненты находятся внутри П. Р.; полуразделённые системы, у к-рых одна из компонент заполняет свою П. Р.; контактные системы - обе компоненты заполняют свои П. Р. В процессе эволюции звёзд одна и та же двойная система может переходить из одного класса в другой.
В полуразделённых и контактных системах наблюдаются газовые потоки, движение к-рых определяется структурой эквипотенциальных поверхностей вне П. Р. С дальнейшим уменьшением
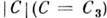две внутр.эквипотенциальные поверхности за П. Р. сливаются в одну гантелеподобную фигуру и при нек-ром значении
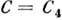наступает пересечение этой фигуры с внеш. эквипотенциальной поверхностью в либрац. точке 
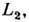к-рая находится за менее массивной компонентой на линии, соединяющей центры масс звёзд. Если вещество газовых потоков обладает достаточной кинетич. энергией, то прежде всего она начнёт уходить из системы через окрестности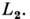 
При ещё меньших значениях
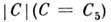наступает пересечение эквипотенциальных поверхностей с внеш. стороны более массивной компоненты в точке 
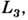после чего эквипотенциальные поверхности разделяются на две фигуры 
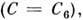расположенные "выше" p "ниже" линии, соединяющей центры масс. Наконец, при нек-ром значении С эти фигуры вырождаются в две точки 
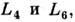носящие назв. треугольных либрац. точек Лагранжа. При любом отношении масс компонент эти точки образуют с центрами масс звёзд равносторонние треугольники 
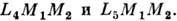Положение точек 
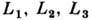на линии, соединяющей центры компонент, зависит от отношения масс. Все либрац. точки являются точками относит. равновесия, т. к. в них 
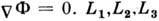- точки неустойчивого равновесия. Ь линейном приближении равновесие в точках 
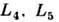устойчиво при условии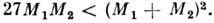 
В системе двух звёзд, обращающихся друг относительно друга по эллиптич. орбитам, гравитац. поле переменно и стационарные эквипотенциальные поверхности отсутствуют. Макс. размеры звёзд здесь ограничены началом истечения вещества под действием переменных приливных сил в момент прохождения пери-астра.
Лит.: Мультон Ф., Введение в небесную механику, пер. с англ., М.-Л., 1936; Мартынов Д. Я., Курс общей астрофизики, 3 изд., М., 1979. Н. И. Шакура.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
