ПЕРЕНОРМИРОВКИ

ПЕРЕНОРМИРОВКИ

(ренормировки) вквантовой теории поля (КТП) - процедура устранения ультрафиолетовыхрасходимостей. П. проводится в процессе решения квантовых ур-ний ив целом представляется в виде особого предписания, формулируемого дополнительнок осн. закону движения - ур-нию Шрёдингера. Др. значение термина "П." связанос конечными изменениями параметров лагранжиана КТП, приводящими к ренормализацииннойгруппе (см. ниже).
УФ-расходимости возникают в квантовополевойтеории возмущений при вычислении интегралов в пространстве 4-импульсовсоответствующих Фейнмана диаграммам, содержащим замкнутые петли. <Путём введения вспомогат. регуляризации такие расходящиеся интегралы делаютсяконечными и вычисляются г. явном виде; при этом в простейших случаях сингулярныесоставляющие выделяются в аддитивные структуры, имеющие вид полиномов невысокойстепени по внеш. импульсам [см. ф-лу (3) в ст. Регуляризация pacсходимостей]. Для нек-рого класса КТП степень этих полиномов не зависит от порядкатеории возмущений и не превышает двух. Такие теории допускают процедуруП., с помощью к-рой удаётся полностью устранить все УФ-расходимости и выразитьрезультаты вычислений через небольшое число параметров, физически близкихпараметрам (массам, константам связи) исходного лагранжиана рассматриваемойсистемы взаимодействующих полей. Эти теории наз. перенормируемыми. В классперенормируемых теорий (с нек-рыми оговорками) входят модели с безразмернымиконстантами связи, в т. ч. теории калибровочных полей, такие как квантовая электродинамика (КЭД) и квантовая хромодинамика (КХД).
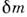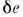В перенормируемых теориях оказываетсявозможным собрать все сингулярные составляющие матричных элементов и Гринафункций в небольшое число структур, к-рые в конечном счёте могут бытьсведены к полевым добавкам к параметрам исходного лагранжиана. В КЭД, напр.,все расходимости сводятся к полевым добавкам и к массеи заряду электрона. Формально эти добавки можно выразить через нек-рыечисловые, обычно сингулярные, множители Z_m и Z_e к исходным (т. н. голым или затравочным) массе т ₀ изаряду e₀: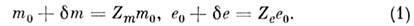

Вычисляемые физ. величины, такие как матричныеэлементы переходов, содержат зависимости только от произведений Z_mm₀ и Z_ee₀. Затравочные масса и заряд, а такжеУФ-сингулярности по отдельности или в к.-л. др. комбинациях в них не входят. <Поэтому возникает возможность отождествить произведения (1) с эксперим.("физическими") значениями массы и заряда электрона:

Z_mm_O =m _физ,Z_ee_O= е _физ.(2)

Эта операция переопределения физ. параметров т _о m _физ= Z_mm_o, e₀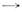e _физ=Z_ee_o(3) путём их умножения на сингулярныемножители, полностью исключающая УФ-расходимости из наблюдаемых физ. величин, <и наз. операцией П. (иногда П. бесконечностей).
Теория П. в КТП была разработана в кон.1940-х - нач. 50-х гг. в трудах Ю. Швингера (J. Schwinger), Р. Фейнмана(R. Feynman), Ф. Дайсона (F. Dyson), А. Салама (A. Salam), Н. Н. Боголюбова.
С качеств. точки зрения изменение масси зарядов частиц под влиянием взаимодействия представляется вполне естественным. <Подобные явления известны из классич. электродинамики: сторонний зарядв среде создаёт вокруг себя облако поляризации, к-рое частично его экранирует. <Поэтому на больших расстояниях эфф. значение наблюдаемого заряда оказываетсяменьше истинного. При перемещении такой частицы вместе с ней движется иоблако поляризации, что приводит к эфф. изменению её инерционных свойств, <т. е. массы. Изменения массы и заряда частицы в этом случае конечны.
В КТП подобная физ. интерпретация соотношенийП. (3) затруднена из-за сингулярного характера констант П.Z_m,Z_c. В отличие от стороннего заряда в поляризуемой среде, <к-рый можно извлечь из среды и исследовать в пустоте, электрон в КТП неможет быть "освобождён" от взаимодействия с квантовым эл.-магн. полем вакуума. <Поэтому входящие в соотношения П. величины m₀, е ₀,Z_m и Z_e не могут быть измерены на опытепо отдельности, а лишь в комбинациях (2). В результате П. получаются конечныеи однозначные выражения, к-рые в ряде случаев описывают эксперимент с чрезвычайновысокой степенью точности. Так, значение аномального магнитного момента электрона, вычисленное в КЭД, совпадает с опытным значением на уровнеэксперим. погрешности порядка 10^-10, что является рекордом вфизике.
Операция устранения расходимостей можетбыть формализована и без использования соотношений П. типа (2), т. к. впространственно-временном представлении УФ-расходимости обусловлены особенностямипропагаторов (одночастичных ф-ций Грина) Штюкель-берга - Фейнмана [Е. С.G. Stueckelberg, 1948; Фейнман. 1949] по переменной квадрата интервалаs² = c²t² - х ² на поверхности светового конуса (s²= 0). Поскольку радиационныепоправки к матричным элементам выражаются в этом представлении черезпроизведения пропагаторов, приходится оперировать с произведениями подобныхсингулярностей, напр. с квадратами дельта-функции Дирака от s².С матем. точки зрения проблема сводится к задаче определения операции умножения обобщённых функций.
Теория умножения обобщённых ф-ций, возникающихв квантовополевых вычислениях, была разработана Н. Н. Боголюбовым в нач.50-х гг. Проблема устранения расходимостей была затем рассмотрена на еёоснове Н. Н. Боголюбовым и О. С. Парасюком. Доказанная ими теорема о П.(см. Боголюбова - Парасюка теорема )с полной матем. строгостью исчерпывающерешает задачу получения конечных однозначных выражений для элементов матрицырассеяния в рамках теории возмущений, без обращения к промежуточной регуляризации, контрчленам и сингулярным соотношениям П. типа (3). Рецептурная часть теории Боголюбова- Парасюка, т. н. R-операция Боголюбова, уже около трёх десятилетийявляется практич. основой получения конечных результатов в перенормируемыхмоделях КТП.
Как отмечалось, термин "П." относитсятакже и к конечным преобразованиям типа (3):

т z_mm, ez_ee,(4)

где z_m, z_e- конечные числа. Возможность и важность таких преобразований конечнойперенормировки, проводимых в квантовополевом формализме после устранениярасходимостей, связаны с неоднозначностью результата процедуры устранениябесконечностей. Анализ структуры этих неоднозначностей, к-рая описываетсяпреобразованиями (4), указывает на существование особой симметрии перенормируемыхвыражений - симметрии, лежащей в основе ренормализац. группы.

Лит.: Боголюбов Н. Н., Ширков Д. <В., Квантовые поля, 2 изд., М., 1991.

Д. В. Ширков.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.