ОРИЕНТАЦИОННЫЕ ФАЗОВЫЕ ПЕРЕХОДЫ

ОРИЕНТАЦИОННЫЕ ФАЗОВЫЕ ПЕРЕХОДЫ

- (спин-переориентационныепереходы) - особый класс магнитных фазовых переходов, при к-рыхменяется ориентация осей лёгкого намагничивания магнетиков при изменениивнеш. параметров (темп-ры, магн. поля). Эти фазовые переходы происходятмежду магнитоупорядоченными фазами магнетика и относятся к т. н. переходамтипа порядок - порядок. При О. ф. и. перестраивается магнитная атомнаяструктура и изменяется магнитная симметрия кристаллов. О. ф. <и., происходящие при изменении темп-ры, наз. спонтанными переходами, приизменении внеш. магн. поля - индуцированными переходами.
Простейшим примером спонтанного О. ф. <п. является наблюдаемая в ряде магн. кристаллов переориентация спинов (спиновыхмагн. моментов) от одной кристаллографич. оси к другой при изменении темп-ры. <Такие переходы наблюдаются, напр., в классич. ферромагнесике кобальте, <в гадолинии, в интерметаллических соединенияхRCo₅ (гдеR - Nd, Pr, Dy, Tb), ферримагнетиках Mn₂Sb и Ba₂Co₂Fe₁₂ О ₂₂ и в целом ряде редкоземельных магнптоупорядоченных кристаллов [1]. Спонтаннаяпереориентация магн. моментов обусловлена в них температурной зависимостьюэнергии магнитной анизотропии.
В том случае, когда переориентация моментовосуществляется в нек-рой кристаллографич. плоскости кристалла, изменениетермодинамич. потенциала Ф кристалла удобно представить в виде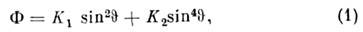

где К ₁ и К₂- константы анизотропии, изменение к-рых с темп-рой и приводит кО. ф. п.; - уголориентации оси лёгкого намагничивания относительно кристаллография, осейв плоскости переориентации. Минимизация (1) по углу приводитк трём возможным состояниям системы (вблизи от О. ф. п. К₂ считают не зависящей от темп-ры):

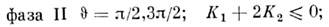
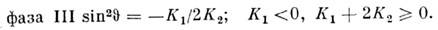
Если К ₁ знакопеременна, <а К₂ > 0 в рассматриваемой области темп-р, то в кристаллемогут существовать коллинеарные фазы I и II и угл. фаза III. Темп-ры Т ₁[при к-рой К ₁(T₁) +2 К₂= 0] и Т₂ [при к-рой К ₁ (Т ₂)= 0] есть точки О. ф. п. II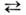IIIи I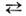III соответственно. <На рис. 1 приведены в качестве примеров температурные зависимости констант К ₁ и К₂ гексагональных интерметаллич. соединений NdCo₅ и РгСо ₅, на рис. 2 показаны температурные зависимости угла отклонениянамагниченности от гексагональной оси для этих соединений. Переходы междуфазами I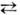111и IIIII, возникающиепри инверсии знака константы анизотропии К ₁, являютсятипичными примерами фазовых переходов, описываемых теорией Ландау [2].

Рис. 1. Температурные зависимости константанизотропии для NdCo₅ (пунктир) и РrСо ₅ (сплошнаялиния).

Действительно, в случае, напр., переходаIIII, разложениетермодинамич. потенциала (1) в ряд по 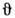вблизи Т = Т ₂ даёт известное выражение теории Ландау[зависимость К ₁( Т) в рассматриваемой области температурпредполагается линейной]: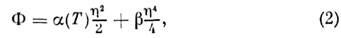

где 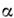( Т)= 2К ₁ (Т) = 2К(Т - Т₂)/Т ₂, К- константа,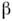= 4 К₂,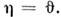Угол здесь играет роль параметра порядка.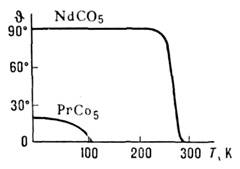

Рис. 2. Температурные зависимости ориентацииосей лёгкого намагничивания для NdCo₅ и РrСо ₅.

Такую же форму принимает термодинамич. <потенциал вблизи точки Т = Т ₁ при (либо 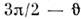).Т. о., переориентация магн. моментов, описываемая термодинамич. потенциалом(1), при К₂ > 0 происходит непрерывно, путём двух фазовыхпереходов 2-го рода при темп-pax Т₁ и Т ₂. Параметр 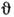(параметр порядка) меняется при этом непрерывно, а производная 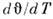имеет разрывы на концах области переориентации (рис. 3, а). Очевидно, <что вблизи темп-р Т ₁ и Т ₂, при к-рыхпроисходят фазовые переходы 2-го рода, должны наблюдаться характерные особенностив поведении ряда термодинамич. величин: теплоёмкости, модуля Юнга и т. <п., а также расходимость восприимчивости (описывающей отклик параметрапорядка на термодинамически сопряжённое ему поле), обращение в нуль частотыколебаний параметра порядка (мягкая мода), замедление его релаксации ит. д. Такие аномалии в окрестности точки О. ф. п. действительно наблюдались, <напр., в редкоземельных магнетиках [1]. При непрерывной переориентациимагн. моментов угл. фаза III играет роль "буфера". Она позволяет магн. <моментам непрерывно переходить из фазы I в фазу II. О. ф. п. относятсяк переходам, для к-рых теория Ландау является очень хорошим приближением, <т. к. флуктуации параметра порядка в критич. состоянии здесь можно не учитывать, <поскольку они проявляются в очень узкой области темп-р (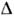.~10^-6 - 10^-8K) вблизи точки перехода.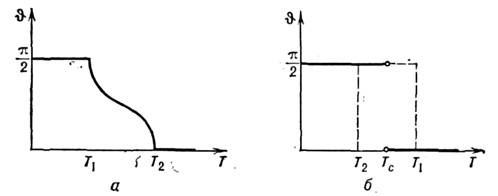

Рис. 3. Температурная зависимость угла 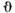при ориентационном фазовом переходе: а - К ₂ б - К ₂< 0.

При К₂ < 0 фаза IIIявляется неустойчивой и температурные области существования фаз I и И перекрываются. <С точки зрения симметрии, непосредств. непрерывный переход IIIневозможен, т. к. для непрерывного перехода необходимо, чтобы группа магн. <симметрии одной из фаз, участвующей в переходе, была подгруппой симметриидругой фазы, что для фаз I и II не выполняется. Следовательно, непосредств. <переход IIIможет осуществляться только скачкообразно (фазовый переход 1-го рода) при .= Т _с, где Т _с определяется условиямиравенства термодинамич. потенциалов обеих фаз: Ф(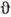= 0) = Ф( 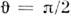),т. е. K₁(T_c) + K₂ =0.Темп-ры Т ₁ и Т₂, определяемые ур-ниями К ₁ (Т ₂)=0 и K₁(T₁)+ 2К ₂= 0, есть границы областей существования метастабильных фаз (в предположении, <что переход IIIпроисходит однородно по образцу). 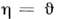Разложение Ф по (либо 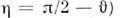приводит к выражению (2), где 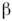= 4 К₂ < 0, что, согласно теории Ландау, является признакомфазового перехода 1-го рода. На рис. 3( б) изображена зависимость 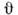( Т )для этого случая.
Внеш. магн. поле Н _вн оказывает существ. влияние на О. ф. п., подавляя их или, наоборот, способствуяих возникновению. Поле Н _вн может также индуцировать О. <ф. п. Напр., в целом ряде антиферромагнетиков при достаточно большом (критическом)значении магн. поля Н _с, приложенного вдоль оси антиферромагнетизма, <происходит переориентация спинов, и намагниченность магн. подрешёток устанавливаетсяперпендикулярно направлению действующего магн. поля [3] (см. Спин-флоппереход). Индуцированные полем О. ф. п. наблюдались также вслабых ферромагнетиках, в частности в редкоземельных ортоферритах, дляк-рых были исследованы разнообразные фазовые диаграммы Н _с-.[1].

Лит.:1) Орнентационные переходыв редкоземельных магнетиках, М., 1979; 2) Ландау Л. Д., Лифшиц Е. М., Статистическаяфизика, ч. 1, 3 изд., М., 1976; 3) Боровик-Романов А. С., Антиферромагнетизм, <в кн.: Итоги науки. Сер. физ.-мат. науки, в. 4, М., 1962.

А. М. Кадомцева.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.