СЛАБЫЙ ФЕРРОМАГНЕТИЗМ

СЛАБЫЙ ФЕРРОМАГНЕТИЗМ

       

существование небольшой (—0,1—10 ед. СГСМ/моль или =102—104 А/(м•моль)) спонтанной намагниченности у определ. классов антиферромаенетиков. Эта намагниченность может возникать в результате нестрогой антипараллельности векторов намагниченности магн. подрешёток антиферромагнетика (поперечный С. ф.) или в результате неравенства величин намагниченности двух антипараллельных подрешёток антиферромагнетика (см. АНТИФЕРРОМАГНЕТИЗМ). Наиболее подробно С. ф. изучен в ромбоэдрич. антиферромагнетиках (a-Fe2O3, MnCO3, NiСO3, CoCO3, FеВО3 и др.), в ортоферритах типа RFeO3 и ортохромитах RСrO3 (R — трёхвалентный ион редкоземельного элемента), в NiF2. У всех известных антиферромагнетиков со С. ф. обнаружен поперечный С. ф. Экспериментально С. ф. наблюдался задолго до открытия антиферромагнетизма, в осн. в гематите (a-Fe2O3); считалось, однако, что он обусловлен наличием примесей ферромагн. окислов железа. Тот факт, что С. ф. наблюдается в химически чистых антиферромагнетиках (без ферромагн. примесей), был установлен впервые для NiF2 в 1955, а для MnCO3 и СоСO3 в 1956. Теоретич. объяснение С. ф. было дано И. Е. Дзялошинским (1957), к-рый показал, что существование С. ф. следует из самых общих представлений о магн. симметрии кристаллов. Теория Дзялошинского, в частности, объясняет, почему в одноосных кристаллах С. ф. наблюдается, когда намагниченность подрешёток направлена перпендикулярно гл. оси симметрии кристалла, и отсутствует, когда намагниченность параллельна этой оси. Эффективное магн. поле, приводящее к С. ф., получило назв. поля Дзялошинского. Оно в 102—104 раз слабее эффективного поля обменного взаимодействия, обусловливающего намагниченность магн. подрешёток кристалла.

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

СЛАБЫЙ ФЕРРОМАГНЕТИЗМ

- существование в антиферромагнетиках спонтанного ферромагн. момента (СФМ), величина к-рого мала по сравнениюс намагниченностью подрешёток. С. ф. существует у большого числа антиферромагнетиков;наблюдался в природных кристаллах гематита 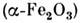задолго до того, как было открыто явление антиферромагнетизма[1].Долгое время считалось, что наблюдаемый ферромагнетизм обусловленпримесями других, ферромагн. окислов железа, пока это явление не было обнаруженов химически чистых образцах NiF₂ [2] (см. табл.), МnСО ₃ и СоСО ₃ [3]. После этого была построена термодинамич. <теория С. ф. в антиферромагнетиках (И. Е. Дзялошинский, 1957, [4]).

Рис. 1. Зависимость молярной намагниченности М _мол монокристаллаМnСО ₃ от внешнего поля H, приложенного вдоль тригональной осиO_z (M_z) и перпендикулярно ей (М _ху) приТ = 4,2К.

Вещества со С. ф. обнаруживают характерную магн. анизотропию. СФМ направленлибо вдоль одного выделенного кристаллографич. направления, либо в плоскости, <перпендикулярной гл. оси тригональных или гексагональных кристаллов (базиснаяплоскость). Типичные кривые намагничивания показаны на рис. 1 на примереМnСO₃. При любом направлении магн. поля Н в базисной плоскости ху возникает параллельная ему намагниченность М _ху, к-рая зависит от H (начиная с полей ~1 кЭ) по закону:

где 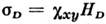- величина СФМ, - магн. восприимчивость в плоскости ху, H_D- эфф.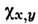поле Дзялошинского. Если вектор H направлен перпендикулярно базиснойплоскости (вдоль оси Oz), то

Величина 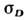составляет небольшую долю от намагниченности подрешёток М _п (п - номер подрешётки). Температурная зависимость ( Т )(рис. 2) аналогична М _п (Т), если в веществепри изменении Т не происходит перехода из одной антиферромагн. структуры(АС) в другую. Для температурной зависимости характерно наличие острого максимума в Нееля точке (Т = Т _N )(рис. 3).

С. ф. возникает в тех антиферромагнетиках, группа магнитной симметрии к-рых допускает одновременно как антиферромагн., так и ферромагн. упорядочение. <Найдены все пространств. и точечные группы магн. симметрии, допускающиесуществование С. ф. [5. 6].

Рис. 2. Температурная зависимость а ₀ для СоСО ₃ (в единицах СГСМ на моль).

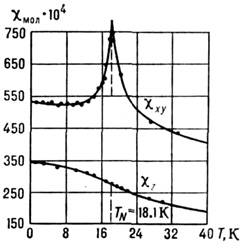
Рис. 3. Температурная зависимость молярной магнитной восприимчивостидля СоСО ₃.

Термодинамическая теория С. ф. основана на разложении термодинамич. <потенциала Ф по компонентам векторов антиферромагнетизма L и намагниченностиМ, являющихся линейными комбинациями М _п (напр., в двухподрешёточномантиферромагнетике L = M₁ - М ₂, М = M₁+ М ₂). Это разложение должно быть инвариантным относительновсех преобразований симметрии пространственной группы кристалла. Многиегруппы допускают в разложении Ф существование членов вида 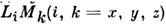. Их наличие приводит к тому, что при установлении антиферромагн. упорядоченияс 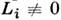возникаетСФМ M_k, величина к-рого может быть рассчитана из ур-ний, <получающихся при минимизации Ф. В случае тригональных структур, обладающихпространственной группой ,

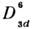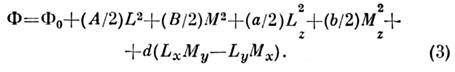
Коэффициенты при изотропных членах ( А к В), обусловленные обменнымвзаимодействием, во много раз больше коэффициентов при анизотропных релятивистскихчленах ( а, b, d). Коэф. В является осн. константой обменноговзаимодействия, определяющей эффективное обменное магн. поле H _Е= BL/2. Минимизация (3) при заданном значении L² даёт два решения:

1)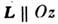(L_x = L_y= 0) и M = 0- такой магн. структурой обладают FeCO₃ и низкотемпературнаямодификация ;

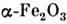2)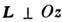и М _х= (d/B)L_y, M_y = (d/B)L_x,M_z = 0. При этом возникает СФМ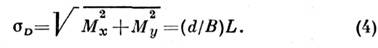

Этот СФМ мал ввиду малости отношения d/B. Такой магн. структуройобладают МnСO₃, СоСО ₃, NiCO₃ и высокотемпературнаямодификация . Если включить в потенциал член с магн. полем, то минимизация Ф приводитк ф-лам (1) и (2), в к-рых 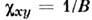,а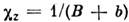

Вектор 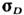перпендикулярен L. Поэтому в веществах со С. ф. векторы намагниченностиподрешёток не направлены строго антипараллельно, а отклоняются на небольшойугол 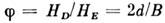от оси антиферромагнетизма (рис. 4, а). В принципе возможен и продольныйС. ф. благодаря различию величин векторов М _п строго антипараллельныхподрешёток. Однако во всех известных случаях С. ф.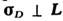. При перемагничивании вместе с 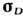должен менять знак и L, т. е. подрешётки должны поворачиваться на180°.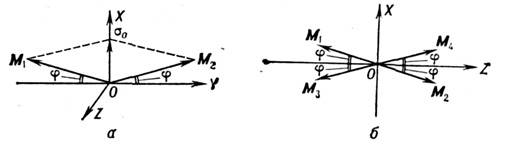

Рис. 4. Образование за счёт скоса векторов намагниченности подрешётокм _п: а - слабого ферромагнетизма в двухподрешёточном антиферромагнетике;б - антиферромагнитной структуры с четырьмя скрещенными подрешётками.

Слагаемое из (3) описывает Дзялошинского взаимодействие, такого вида членывстречаются в ряде пространственных групп тригональных, тетрагональныхи гексагональных сингоний. В нек-рых группах тетрагональных сингоний С. <ф. описывается членом вида 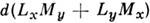,а в ромбич. сингониях - членом вида . В моноклинных сингониях подобная 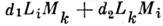сумма содержит четыре члена. В большинстве групп гексагональной и кубическойсингоний С. ф. описывается членами шестого и четвёртого порядка по 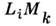[5].

Для антиферромагнетиков с четырьмя и более подрешётками существует неск. <векторов L, описывающих разл. антиферромагн. структуры АС. Поэтомув выражение для потенциала Ф могут входить члены типа 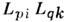( р, q - номера АС), к-рые приводят к возникновению АС со скрещеннымиподрешётками, не обладающих С. ф. (рис. 4, б).

В микроскопической теории С. ф. рассматривают самый общий вид спинового гамильтониана, удовлетворяющий симметрии данного кристалла:

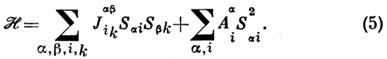
Здесь 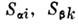- операторы компонент спинов магн. ионов, расположенных в узлах 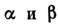; 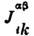-тензор, описывающий их взаимодействие; 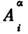-константа одноионной анизотропии. Первый член содержит как обычную изотропнуючасть (i= k), к-рая описывает обменное взаимодействие, таки анизотропную часть 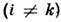. Последняя описывает анизотропию, обусловленную межионным взаимодействием, <а также С. ф. Ответственная за С. ф. часть гамильтониана может быть представленав виде 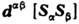. Вектор Дзялошинского 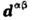соответствует константе а в разложении (3). В рассмотренных вышетригональных кристаллах 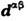направлен параллельно оси .

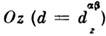Второй член описывает одноионную анизотропию, и обычно коэф.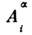независят от номера узла. Однако в нек-рых тетрагональных кристаллах осисимметрии в двух эквивалентных узлах элементарной ячейки повёрнуты на 90°и соответственно 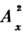.В этом случае С. ф. обусловлен 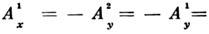не анизотропным обменом, а одноионной анизотропией.

Фазовые переходы. В отличие от обычных антиферромагнетиков, в антиферромагнетикахсо С. ф. при Т > T_N магн. поле вызывает антиферромагн. <упорядочение с вектором L, перпендикулярным приложенному полю. Подобноферромагнетикам у антиферромагнетиков со С. ф. в магн. поле (параллельномС. ф. моменту) нет различия в магн. симметрии при темп-pax выше и нижекритической [9]. С этим обстоятельством связано возникновение показанногона рис. 3 пика магн. восприимчивости.

В кристаллах, у к-рых симметрия допускает существование С. ф., наблюдаютсяспецифич. магнитные фазовые переходы. Во-первых, переходы, обусловленныеизменением с темп-рой соотношения констант магн. анизотропии, приводящиек повороту L от одного кристаллографич. направления к другому. Врезультате такого поворота антиферромагнетик может переходить из состояниясо С. ф. в чисто антиферромагн. состояние (переход Морина в 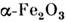) или в состояние, где С. ф. сохраняется, но происходит соответствующийповорот вектора СФМ. Подобные ориентационные фазовые переходы внек-рых ортоферритах и ортохромитах происходят постепенно, и процесс переориентацииограничен сверху и снизу по темп-ре двумя фазовыми переходами 2-го рода[7]. Во-вторых, наблюдаются фазовые переходы из чисто антиферромагн. состоянияв состояние со С. ф. под действием магн. поля. Такие переходы происходятв легкоосных антиферромагнетиках, если Н приложено перпендикулярнолёгкой оси. Магн. поле вызывает поворот вектора L в плоскости, перпендикулярной Н, и возникновение СФМ вдоль Н. В четырёхподрешёточных антиферромагнетикахвозможен индуцированный магн. полем переход 1-го рода в состояние со С. <ф., сопровождающийся перестройкой АС.

В веществах, симметрия к-рых допускает существованне С. ф., но анизотропиятакова, что вещество переходит в чисто антиферромагн. состояние, в областивблизи T_N могут наблюдаться аномалии в температурнойзависимости восприимчивости, аналогичные показанной на рис. 3.

Свойства некоторых антиферромагнетиков со слабым ферромагнетизмом

Лит.:1) S m i t h I., The magnetic properties of hematite, «Phys.Rev.», 1916, v. 8, p. 721; 2) Matarrese L. M., Stout J. W., Magnetic anisotropyof NiF₂, «Phys. Rev.», 1954, v. 94, p. 1792; 3) Боровик-РомановА. С., Орлова М. П., Магнитные свойства карбонатов кобальта и марганца,«ЖЭТФ», 1956, т. 31, с. 579; 4) Дзялошинский И. Е., Термодинамическая теория«слабого» ферромагнетизма антиферромагнетиков, «ЖЭТФ», 1957, т. 32, с.1547; 5) Т у р о в Е. А., Физические свойства магнитоупорядоченных кристаллов, <М., 1963; 6) В i г s s R., Symmetry and magnetism, Amst., 1964; 7) Ориентационныепереходы в редкоземельных магнетиках, М., 1979; 8) Moriya Т., Weak ferromagnetism,в кн.: Magnetism, ed. by G. T. Rado, H. Suhl, v. 1, N. Y.-L., 1963; 9)Боровик-Романов А. С., Лекции по низкотемпературному магнетизму, Новосиб.,1976. А. С. Боровик-Романов.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.