ОБОБЩЁННАЯ ВОСПРИИМЧИВОСТЬ

ОБОБЩЁННАЯ ВОСПРИИМЧИВОСТЬ

- характеристикаотклика системы на внеш. воздействие. Внеш. силы (механич., электрич.,магн.), соответствующие этому воздействию, описываются добавлением к гамильтониану Н₀ системы, на к-рую воздействуют, члена вида xF(t), где в классич. <случае х - обобщённая координата системы, в квантовом случае - соответствующийоператор, F(t) - обобщённая сила, связанная с этой координатой (сопряжённаяей). Обобщённая сила определяется только внеш. условиями, она не зависитот свойств системы и является заданной ф-цией времени как в классическом, <так и в квантовом случае.
О. в. (ф-ции отклика) на воздействие обладаютрядом свойств, не зависящих от конкретного вида внеш. воздействия (напр.,свойством аналитичности), что позволяет получить для них общие выражения. <Кроме того, через О. в. выражаются нек-рые характеристики системы в отсутствиевнеш. поля. Предполагается, что в отсутствие внеш. поля квантовомеханич. <среднее значение Тогда линейная связь между и обобщённой силой F(t )выражается через ф-цию

Отклик не может зависеть от F(t' )в моменты времени t < t', т. <е.при t< t', что является выражением причинности принципа. Выполнивпреобразование Фурье, получим

Ф-ция определяющая поведение системы под действием внеш. поля, наз. О. в. Иногдавводят также обобщённый адмиттанс и обобщённый импеданс
О. в.является в общем случае комплексной величиной:Поскольку величины и F(t )действительны, получаем:и Мнимаячасть О. в. связана с диссипацией энергии в системе. Если на систему действуетмонохроматич. поле то потери Q в единицу времени равны

Т. к. в устойчивых системах возможна толькодиссипация энергии (Q
Матем. выражением принципа причинностиявляется отсутствие полюсов у О. в. в верх. полуплоскости комплексной частоты. <Это означает, что ф-ци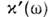и и удовлетворяют дисперсионнымсоотношениям

Здесь Р - символ главного значенияинтеграла и предполагается, что при Из дисперсионных соотношений и положительности следует, что статическая величина положительна:

В общем случае, когда О. в. зависит нетолько от времени, но и от координат (пространств. дисперсия), необходимоучитывать релятивистский принцип причинности: причина не может влиять наследствие, если их мировые точки разделены пространственноподобным интервалом. <Поэтому в однородной системе для фурье-образа О. в. (где q - волновой вектор) получим:

где параметр и пробегает значения .< с, <с - скорость света в вакууме ( и =0 соответствует обычным дисперсионнымсоотношениям).
Для определения О. в. по микроскопич. <свойствам системы обычно используют Кубо формулу

(здесь [а, в]обозначаеткоммутатор величин а и в), откуда можно получить т. н. спектральноепредставление для О. в.:

где - матричный элемент перехода из состояния с энергией в состояние с энергией а - соответствующая частота.
Мнимая часть О. в. (а следовательно, идиссипация энергии) связана с флуктуациями величины х при темп-ре . (т. <н. флуктуационно-диссипативная теорема):

Для неск. флуктуирующих величин х _i этатеорема обобщается следующим образом:

Отсюда можно получить важные соотношениясимметрии для О. в. В отсутствие внеш. магн. поля Н: При наличии магн. поля где и принимаютзначения в зависимости от того, как меняются знаки величин x_i и x_k приобращении времени. Эти соотношения можно рассматривать как обобщение принципасимметрии кинетич. коэф. (см. Онсагера теорема).

Лит.: Ландау Л. Д., Лифшиц Е. М.,Статистическая физика, ч. 1, 3 изд., М., 1976; Зубарев Д. Н., Неравновеснаястатистическая термодинамика, М., 1971.

О. В. Долгов.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.