- ФЛУКТУАЦИОННО-ДИССИПАТИВНАЯ ТЕОРЕМА
- ФЛУКТУАЦИОННО-ДИССИПАТИВНАЯ ТЕОРЕМА
-
- устанавливает связь между спектром флуктуации физ. величин в равновесной диссипативной среде и её обобщёнными восприимчивостями, т. е. параметрами, характеризующими её реакцию на внеш. воздействие. Классич. пример Ф.-д. т.- Найквиста формула, связывающая спектральную мощность флуктуации напряжения проводника, или 1. н. эдс шума г ш, с его сопротивлением R:
где
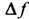-полоса частот.Соотношение (1) можно обобщить на случай любой квантовой системы. Пусть внеш. воздействие на систему описывается включением в гамильтониан возмущающего оператора:
обобщённая восприимчивость а вводится соотношением
связывающим фурье-компоненты силы
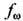и усреднённой физ. величины 
(
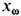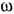-циклич. частота). Флуктуации величины х обычно характеризуются корреляц. ф-цией: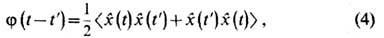
где скобки означают статистич. среднее от гейзенберговских операторов. Ф.-д. т. в этом случае может быть представлена в виде следующего соотношения:
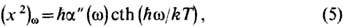
где
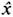-оператор нек-рой физ. величины, характеризующей систему, a f (t)- возмущающая обобщённая сила. Тогда где
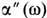-мнимая часть обобщённой восприимчивости, а 
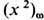- спектральная мощность флуктуации, фурье-ком-понента коррелятора (4). В основе (5) лежит принцип OH-сагера, согласно к-рому как малое отклонение системы от термодинамич. равновесия, вызванное внеш. силой, так и флуктуация релаксируют к равновесию одинаковым образом (см. Онсагера теорема).При отклонении системы от равновесного состояния (напр., при помещении полупроводника во внеш. электрич. поле) ф-ла Найквиста нарушается. Для слабо неравновесного случая в соотношении (1) заменяют T на нек-рый параметр Т ш - т. н. шумовую температуру, так что в этом случае ф-ла (1) служит определением феноменологич. параметра T ш, являющегося удобной характеристикой флуктуации неравновесной системы.
Лит.: Ландау Л. Д., Лифшиц E. M., Статистическая физика, ч. 1, 3 изд., M., 1976, гл. 12; Климонтович Ю. Л., Статистическая физика, M., 1982, гл. 24.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
