- КВАТЕРНИОНЫ
- КВАТЕРНИОНЫ
-
- элементы множества И, представимые в виде
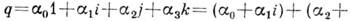
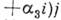. Здесь 
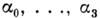- веществ, числа, а (1, г, /, k)- образующие базиса в Н, удовлетворяющие соотношениям:
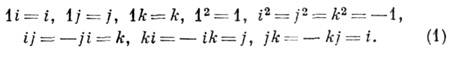
Обозначения принадлежат У. Гамильтону (W. R. Hamilton), открывшему К. в 1843. В его честь для обозначения множества всех К. употребляется буква Н. Соотношение (1) можно записать в более компактной форме: пусть е 0, e1 , е 2, е 3 - образующие, тогда
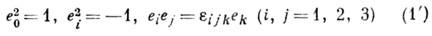
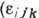- Леви-Чивиты символ).
Умножение К. q на скаляр a и сложение К. определяются так же, как и для обычных векторов. Можно ввести произведение двух К.
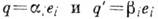ф-лой 
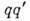= (иногда выделяют скалярную и векторную части 
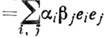К.: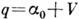 
, тогда умножение векторных частей определяется ф-лой V1V2=-(V1V2)+[V1V2]). Тем самым множество H превращается в алгебру (алгебру кватернионов). Из соотношений (1) следует, что Н - некоммутативная, но ассоциативная алгебра. Алгебра Н содержит в виде подалгебры поле веществ. чисел R=
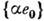и поле комплексных чисел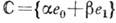 
Алгебра Н допускает изоморфное матричное представление с помощью Паули матриц:
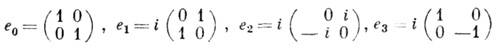
(здесь
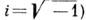
Для каждого К.
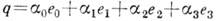определён сопряжённый К. 
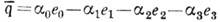и норма 
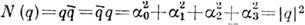Обратным кватернионом является 
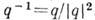. Каждый ненулевой К. имеет обратный. Алгебра с таким свойством называется алгеброй с делением. Алгебра Н (наряду с полями R и С) является единств. ассоциативной алгеброй с делением (теорема Фробениуса). Список алгебр с делением замыкает алгебра октонионов (октав, чисел Кэли) - 8-мерная алгебра, в к-рой нарушена ассоциативность произведения. Наряду с веществ. и комплексными числами в разл. вопросах теории представлений групп, топологии и физики можно использовать К. Вращение трёхмерного пространства можно задать при помощи К. с нормой 1 (аналогично тому, как вращение плоскости задаётся комплексным числом с модулем 1).
Лит.: Дубровин Б. А., Новиков С. П., Фоменко А. Т., Современная геометрия, 2 изд., М., 1986; Казакова Г., Векторная алгебра, пер. с англ., М., 1979.
М. И. Монастырский.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
