- ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ
- ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ
-
- интегральные представления ф-ций отклика, описывающих реакцию равновесной стационарной физ. системы на внеш. воздействия. Д. с. отражают аналитич. свойства ф-ций отклика в комплексной плоскости частоты (энергии), фиксируют их частотную зависимость и приводят к ряду ограничивающих их неравенств, правил сумм и т. п. В более узком смысле Д. с. связывают рефракцию распространяющихся в системе волн с их поглощением; сюда же относятся Д. с. для процессов рассеяния в квантовой механике и квантовой теории поля. Д. с. имеют универсальный вид, не зависящий от конкретной дииамики системы, и используются во мн. разделах физики: в динамике диспергирующих сред (отсюда назв. Д. с.), в физике элементарных частиц и др.
Вывод Д. с. не требует сведений о структуре и динамике системы, а основан на общем причинности принципе: "никакое физ. событие не может повлиять на уже происшедшие события". Соответственно, реакция системы в момент времени t на воздействие в момент t' описывается ф-цией отклика
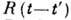 , равной нулю при t<t', а фурье-компонента
, равной нулю при t<t', а фурье-компонента 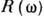 этой ф-ции конечна и потому аналитична в верхней полуплоскости частоты
этой ф-ции конечна и потому аналитична в верхней полуплоскости частоты 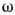 . Использование Коши интеграла приводит к простейшему безвычитательному Д. с. (см. также Гильберта преобразование):
. Использование Коши интеграла приводит к простейшему безвычитательному Д. с. (см. также Гильберта преобразование):
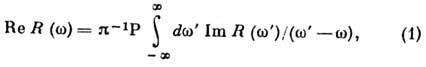
справедливому, если
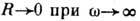 . Здесь P - символ главного значения интеграла. Для полиномиально растущих с
. Здесь P - символ главного значения интеграла. Для полиномиально растущих с 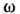 ф-ций
ф-ций 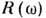 в (1) входит отношение
в (1) входит отношение 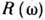 к полиному соответствующей степени
к полиному соответствующей степени 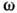 , что даёт Д. с. "с вычитаниями"; именно так строятся перенормированные Д. с. в квантовой теории поля. Реальный вывод Д. с. в большинстве случаев гораздо сложнее приведённой схемы из-за необходимости учёта ряда факторов: дополнит. аргументов ф-ции отклика, требований релятивистского принципа причинности ("не влияют друг на друга также события, связанные пространственноподобным вектором") и др.
, что даёт Д. с. "с вычитаниями"; именно так строятся перенормированные Д. с. в квантовой теории поля. Реальный вывод Д. с. в большинстве случаев гораздо сложнее приведённой схемы из-за необходимости учёта ряда факторов: дополнит. аргументов ф-ции отклика, требований релятивистского принципа причинности ("не влияют друг на друга также события, связанные пространственноподобным вектором") и др.
Исторически первыми Д. с. были Крамерса - Кронига соотношения, связывающие действит. и мнимую части показателя преломления среды, к-рая обладает частотной дисперсией. Более общие Д. с., охватывающие и случай пространственной дисперсии, имеют вид (1) с заменой R величинами
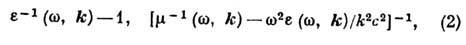
прямо связанными с продольной и поперечной Грина функциями эл.-магн. поля в однородной изотропной среде (
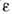 и
и 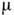 - диэлектрич. и магн. проницаемости, k - волновой вектор). Д. с. для величины
- диэлектрич. и магн. проницаемости, k - волновой вектор). Д. с. для величины 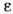 , когда
, когда 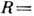
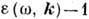 , справедливы лишь в пределе k=0, в к-ром эта величина становится ф-цией отклика. Релятивистскому принципу причинности отвечают Д. с., введённые M. А. Леонтовичем в 1961 и отличающиеся от Д. с. для величин (2) заменой в правой части
, справедливы лишь в пределе k=0, в к-ром эта величина становится ф-цией отклика. Релятивистскому принципу причинности отвечают Д. с., введённые M. А. Леонтовичем в 1961 и отличающиеся от Д. с. для величин (2) заменой в правой части 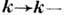
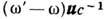 (
(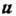 - произвольный вектор,
- произвольный вектор,  ). В сочетании с флуктуационно-диссипативной теоремой, связывающей
). В сочетании с флуктуационно-диссипативной теоремой, связывающей 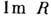 с процессами диссипации в среде, Д. с. дают информацию об общих свойствах последней (см. также Кубо формулы).
с процессами диссипации в среде, Д. с. дают информацию об общих свойствах последней (см. также Кубо формулы).
Д. с. для ф-ций Грина важны также в квантовой теории многих тел и к-вантовой теории поля. Д. с. для фейнмановской одночастичной ф-ции Грина ферми-системы при T=0 имеет вид (1) с добавлением фактора
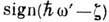 под интегралом, переходящего в
под интегралом, переходящего в 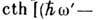
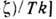 при конечной темп-ре T,
при конечной темп-ре T,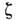 - хим. потенциал. Д. с. для фейнмановской ф-ции Грина D(z )квантованного скалярного поля даётся спектральным представлением
- хим. потенциал. Д. с. для фейнмановской ф-ции Грина D(z )квантованного скалярного поля даётся спектральным представлением 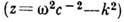 :
:
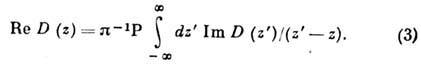
В квантовой теории поля большое значение имеют также Д. с. для более сложных, чем ф-ции Грина, ф-ций отклика: формфакторов, амплитуд рассеяния и др. Особую роль играют Д. с. для амплитуды упругого рассеяния вперёд, связывающие, в силу оптической теоремы, непосредственно наблюдаемые величины: действит. часть амплитуды и полное сечение рассеяния. Эксперим. проверка Д. с., выведенных непосредственно из общих принципов квантовой теории поля, показала применимость этих принципов вплоть до масштабов ~10-16 см. Д. с. послужили исходным пунктом целого ряда методов описания сильного взаимодействия (см. Дисперсионных соотношений метод). Однако они в значит. мере утратили свою исключит. роль в связи с успехами квантовой хромодинамики как динамич. теории сильного взаимодействия.
Лит.: Агранович В. M., Гинзбург В. Л., Кристаллооптика с учетом пространственной дисперсии и теория экситонов, 2 изд., M., 1979; Бартон Г., Дисперсионные методы в теории поля, пер. с англ., M., 1968; Hуссенцвейг X. M., Причинность и дисперсионные соотношения, пер. с англ., M.. 1976. Д. А. Киржниц.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
