ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ЯДРА

ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ЯДРА

- коллективное движение нуклонов в ядре, связанное с изменением ориентации ядра в пространстве. В. д. я. обусловлено несферичностью его равновесной формы (см. Деформированные ядра). В. д. я., предсказанное О. Бором (A. Bohr) и Б. Моттельсоном (В. R. Mottelson) в 1952, открыто в 1953.

В. д. я. соответствует последовательность уровней с энергией e , увеличивающейся с ростом полного угл. момента I уровня пропорционально I(I+1). Совокупность таких уровней образует вращат. полосу. Для тяжёлых ядер вероятность электрич. квадрупольных ( Е2 )радиац. переходов между соседними вращат. уровнями в полосе больше вероятности одночастичных Е2 -переходов в 100 раз (см, Оболочечная модель ядра, Мулътипольное излучение. Гамма-излучение). Число уровней в полосе может быть большим. Так, в ядре ¹⁶⁸Hf низшая вращат. полоса прослежена до уровня с I=34 и энергией =10,5 МэВ.

Возбуждение вращат. уровней осуществляется электрич. полем иона, налетающего на ядро ( кулоновское возбуждение ядер), и в ядерных реакциях с тяжёлыми ионами (HI). В первом случае сечение возбуждения пропорц. вероятности Е2 -перехода. Если на ядро налетает тяжёлый ион (HI), то возможно многократное кулоновское возбуждение, при к-ром заселяются уровни вращательной полосы с большим I (напр., до I=26 для ионов ²⁰⁸Pв) (см. Высокоспиновые состояния ядер). В ядерных реакциях типа (HI; хп, )заселение уровней происходит сверху при распаде составного ядра.

Вращат. полосы обнаружены у мн. ядер, начиная с ⁸Be. Наиб. изучены вращат. состояния ядер с числом нуклонов 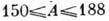(лаетоноиды) и А>224 (актиноиды), имеющие в осн. состоянии большую аксиально-симметричную деформацию. В этих ядрах приближённо можно отделить вращат. движение от внутреннего колебательного и одночастичного. При этом каждому внутр. состоянию ядра в его спектре соответствует вращат. полоса с определ. последовательностью I и пространств. четностью, совпадающей с чётностью внутр. состояния, на к-ром полоса основана.

Рис. 1. Схема связи угловых моментов в медленно вращающемся аксиально-деформированной ядре.

Интерпретация вращательных спектров. Если рассматривать ядро как твёрдое тело, то его вращение описывается с помощью трёх Эйлера углов, определяющих ориентацию собственной системы координат 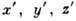, жёстко связанной с ядром, относительно лабораторной системы координат х, у, z. Ось z' направлена вдоль оси симметрии ядра (рис. 1). Т. <к. квант. вращение вокруг этой оси невозможно, то гамильтониан вращат. движения имеет вид

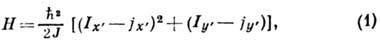
где I - оператор полного угл. момента;- его часть, обусловленная внутр. движением нуклонов; J - момент инерции ядра. Из гамильтониана можно выделить чисто вращат. часть :

и энергию взаимодействия Кориолиса

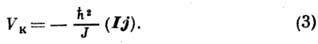
Состояние вращат. движения описывается тремя квантовыми числами: угл. моментом I, его проекцией M на ось z и проекцией К на ось z'. Внутр. движение нуклонов характеризуется проекцией 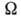угл. момента на ось z' . Условие аксиальной симметрии обеспечивает равенство . Кроме того, угл. момент коллективного вращения перпендикулярен z', а составляющая вдоль z' обусловлена только орбитальным движением нуклонов (рис. 1). Отсюда следует, что для вращат. полосы . Следствием аксиальной симметрии является также инвариантность относительно поворота на 180° вокруг любой оси, перпендикулярной z' (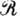 -инвариантность). Это приводит к существованию дополнит. квантового числа, наз. сигнатурой, в соответствии с к-рым различают 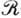-чётные и -нечётные уровни.

Вращательные полосы четно-чётных ядер основаны на состояниях с K=0,1, 2, ... Простейшую структуру имеют полосы с K=0⁺, к которым относится полоса основного состояния. Вследствие 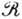-инвариантности эти полосы содержат уровни только с чётными I. Их энергии

В полосах осн. состояния хорошо деформированных ядер (4) выполняется с точностью до неск. десятых процента для уровней с небольшими I (для лантоноидов ==30 кэВ, для актиноидов - 15 кэВ). Низшие вращат. полосы ядер с нечётным числом нуклонов основаны на состояниях последней нечётной частицы в несферич. потенциале. Поэтому квантовые числа К,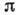уровней определяются нечётного нуклона. Полоса содержит уровни с I=K, К+1, К+2,... (К - нечётное). Энергия низших уровней в полосе описывается ф-лой (4), но с меньшей точностью, что обусловлено смешиванием полос, основанных на разл. однонуклонных состояниях, из-за взаимодействия Кориолиса (3). Особенно сильно искажены полосы, основанные на состояниях нечётного нуклона, принадлежащих подоболочке с большим j и с . Для последних энергия низших уровней

где а, наз. параметром развязывания, зависит от структуры ядра.

Вращат. полосы нечётно-нечётных ядер менее изучены. По-видимому, каждой конфигурации нечётных нейтрона и протона соответствуют 2 полосы с и 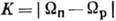. Если 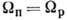, то полоса с К=0 расщепляется на две с уровнями противоположной -чётности; -чётная полоса имеет чётную последовательность I, -нечётная -нечётную.

Электромагнитные переходы во вращательных спектрах. Адиабатичность приводит к ряду закономерностей для вероятности эл.-магн. переходов. Вероятность испускания -квантов мультипольности L:

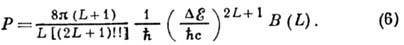
Здесь - разность энергий начального (i) и конечного (f) состояний, B(L)- приведённая вероятность перехода, зависящая от структуры этих состояний. При этом должны выполняться правила отбора для I и :

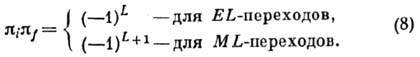
Эл.-магн. переходы происходят либо внутри вращат. полосы, либо между уровнями разл. полос. В первом случае согласно (7) и (8) могут происходить либо только переходы E2, если 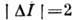, либо Е2 и М1, если . T. к. внутр. состояния ядра остаются неизменными, то вероятности переходов зависят только от коллективных переменных. Так, вероятность Е2- перехода

где величина в скобках - Клебша- Гордана коэффи циент, описывающий сложение угл. моментов в собств. системе координат, Q₀ - внутр. квадруполъный электрический момент ядра. Ядра лантоноидов с параметром квадрупольной деформации 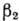~0,3 имеют Q₀~8*10^-24 см ². Для состояний с наиб. вероятные переходы с =2 происходят между уровнями с одинаковой сигнатурой. Переходы с =1 между уровнями с разной сигнатурой в (A/I)² раз менее вероятны. Из (9) следует, что отношение вероятностей Е2 -переходов определяется только геом. фактором сложения угл. моментов начального и конечного состояний. Эти правила для низших вращат. уровней хорошо деформированных ядер выполняются с точностью до неск. процентов.

Переходы M1 зависят не только от коллективного гиромагн. отношения g_R (см. ниже), но и от внутр. g-фактора (g_K )нуклонов. Для полос с приведённые вероятности М1 -переходов:

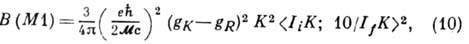
где - масса нуклона (в полосе с 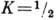В зависит дополнительно от т. <н. магн. параметра развязывания). Соотношение (10) выполняется для низших уровней полос с 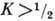с точностью до неск. процентов. Измеряя вероятности М1 -перехода и зная статич. магн. момент ядра, можно найти g_R для нечётных ядер. Для низших состояний четно-чётных ядер g_R находят по величине статич. магн. момента, определяемого по прецессии возбуждённого состояния 2⁺ в магн. поле (см. Ядерный магнитный резонанс).

Переходы между уровнями разл. полос менее вероятны, т. к. происходят между разл. одночастичными состояниями. Для них возникает дополнит. правило отбора:

к-рое является следствием приближённого сохранения К. Переходы, для к-рых условие (11) не выполняется, наз. К- запрещёнными, а величина 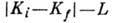наз. порядком К -запрета. Хотя правило (11) не является строгим из-за приближённого характера адиабатичности (см. ниже), тем не менее интенсивность К -запрещённых переходов ослаблена (~в 10² на каждый порядок К- запрета).

Существование в деформированных ядрах приближённых (асимптотич.) квантовых чисел 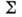(где - гл. осцилляторное квантовое число; - квантовое число, определяющее колебание нуклона вдоль оси ; - в плоскости, перпендикулярной ; - проекция орбитального момента нуклонов на - проекция спина нуклона на ) также приводит к дополнит. правилам отбора для вероятностей одночастичных переходов (табл.).

	Асимптотические правила отбора для "облегчённых" дипольных переходов
	Переход
	Е1	0	b1	b1	0	0
	"	b1	b1	0	b1	0
	Мl	0	0	0	0	0
	"	b1	0	0	0	b1
	"	b1	0	b1	b1	0

Правила отбора по асимптотич. квантовым числам не являются строгими. Однако их нарушение в "затруднённых" переходах уменьшает вероятность последних в 10-100 раз по сравнению с "облегчёнными" переходами.

Отношение приведённых вероятностей двух эл.-магн. переходов мультипольности L с уровня I_iK_i одной полосы на уровн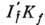и и другой полосы, если 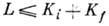или если К _i или K_j=0:

Если К _i=К _f, соотношение (12) переходит в правило интенсивностей эл.-магн. переходов внутри полосы.

Соотношение (12) выполняется и для облегчённых переходов и ядерных реакций передачи нуклонов. Оно является критерием адиабатичности вращения.

Коллективные параметры. Абс. величины энергий уровней и вероятностей переходов E2 и М1 зависят от 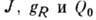. Эти параметры определяются внутр. структурой ядра и, оставаясь приближённо постоянными внутри полосы (для не слишком больших I), плавно изменяются от ядра к ядру, а в данном ядре - от одной полосы к другой.

Момент инерции J вращающегося ядра можно рассматривать как его реакцию на силы Кориолиса, искажающие движение нуклонов в ср. поле. Сильное влияние на J оказывает взаимодействие нуклонов, приводящее к парным корреляциям сверхпроводящего типа. В деформир. ядрах пару образуют нуклоны с противоположным знаком . В четно-чётных ядрах парные корреляции приводят к характерному спектру одночастичных возбуждений со щелью ( 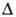- энергия корреляции пары). Они мешают нуклонам участвовать во вращении, уменьшая J приблизительно вдвое по сравнению с твердотельным значением:

где

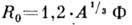- среднеквадратичный радиус ядра, - параметр квадрупольной деформации (ядро - эллипсоид вращения с полуосями а>b). Для системы невзаимодействующих нуклонов, движущихся в ср. поле, J=J _Т. Для нечётных и нечётно-нечётных ядер J низших полос в ср. на 20% больше, чем у осн. состояний соседних четно-чётных ядер. Это отличив объясняется уменьшением 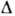и взаимодействием Кориолиса между одночастичными состояниями.

Парными корреляциями объясняется и отличие величины g_R от значения Z/A, к-рое получилось бы для равномерно заряженного вращающегося твёрдого тела. Для протонов больше, чем для нейтронов, поэтому протоны менее эффективно участвуют во вращении. Это уменьшает g_R по сравнению с Z/A~на 20%.

Отклонения от адиабатичности. В действительности адиабатичность вращения нарушается уже в самом начале полосы. Однако отклонения невелики. Так, энергия уровней с во вращат. полосе с K=0 чётно-чётного ядра

причём отношение постоянных 10^-3 для осн. состояний хорошо деформированных ядер.

Осн. источник неадиабатичности ядерного вращения-сила Кориолиса (3). Для нуклона вблизи ферми-поверхности 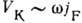, где -частота вращения ядра, 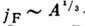- макс. момент нуклонов у поверхности Ферми. В деформир. ядрах для пары нуклонов Поэтому осн. параметр неадиабатичности

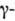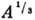Др. параметры: ( -энергия нуклона на поверхности Ферми), описывающий взаимодействие вращения с деформацией; , описывающий взаимодействие вращения с и колебаниями (см. Колебательные возбуждения ядер) с частотой (в раз меньше 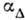). Эффекты центробежного растяжения ядра также несущественны для 10, Деформация ядра начинает заметно изменяться, когда центробежная энергия вращения сравнивается с оболочечной, что происходит при .

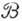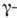T. о., во вращат. спектрах четно-чётных ядер коэф. в осн. обусловлен парными корреляциями нуклонов. Вклад в от взаимодействия вращат. и колебат. движений в раз меньше. Heадиабатичность вращения по отношению к и колебаниям проявляется в нарушении (12) для переходов между уровнями этих полос и осн. полосы.

Др. способ описания неадиабатич. эффектов - модель перем. момента инерции J, к-рая для вращат. полосы осн. состояния хорошо описывает энергии вращат. уровней до I=12. При больших I наблюдается неадиабатич. эффект, наз. аномалией вращат. спектра. А. Джонсон (A. Johnson) в 1971 обнаружил отклонение энергий переходов от правила интервалов (4). Впоследствии было установлено, что это явление носит общий характер. Оказалось, что энергии переходов между соседними уровнями в полосе в интервале 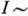12-16 не растут монотонно с I, а остаются неизменными и даже уменьшаются, что соответствует резкому увеличению J. Это можно представить в виде S-образной зависимости 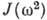(рис. 2) - отсюда термин бэкбендинг("обратный загиб").

Аномалии вращат. спектра четно-чётных ядер редкоземельных элементов при I~12-16 связаны с пересечением полосы осн. состояния с полосой, основанной на нейтронном двухквазичастичном возбуждении из подоболочки . Благодаря большому одночастичному моменту силы Кориолиса изменяют схему сложения угл. моментов в последней полосе. Суммарный момент 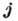двухквазичастичного возбуждения "развязывается" с деформацией и ориентируется преим. вдоль оси вращения ядра (рис. 3). Аномалии вращат. спектра в нечётных ядрах наблюдаются при несколько больших I в полосах, основанных на нейтронном состоянии из подоболочки 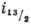и при тех же I в остальных низколежащих полосах.

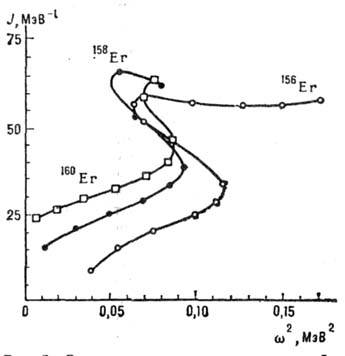
Рис. 2. Зависимость момента инерции J ядра от частоты его вращения в четно-чётных изотопах Er.

Рис. 3. Схема связи угловых моментов в выстроенной полосе.

При большей энергии в области I~26-30 наблюдается 2-й бэкбендинг. Он объясняется пересечением нейтронной двухквазичастичной полосы с полосой, основанной на протонном двухквазичастичном возбуждении из подоболочки . При больших I "в игру вступают" ещё более возбуждённые полосы. T. о., низшая по энергии, т. н. осн. ираст-полоса, состоит из частей разл. полос. Каждая полоса вносит в I свою одночастичную часть, приблизительно равную угл. моменту возбуждённого состояния, на к-ром она основана. Следовательно, угл. момент ираст-полосы образован как коллективным вращением ядра, так и одночастичным движением нуклонов (см. Высокоспиновые состояния ядер). Лит.: Бор О., Вращательное движение в ядрах, пер. с англ., "УФН", 1976, т. 120, с. 543; Бор О., Mоттельсон Б., Структура атомного ядра, пер. с англ., т. 2, M., 1977; Павличенков И. M., Аномалии вращательных спектров деформированных атомных ядер, "УФН", 1981, т. 133, с. 193.

И. M. Павличенков.

Угловое распределение истинно вторичных электронов 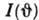при 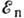>1 кэВ и 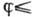60-85° приблизительно косинусоидальное. При 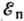>0,1 кэВ (независимо от ) угл. распределение упруго отражённых электронов (рис. 7) обладает такой же дифракц. структурой, зависящей от и Z, как и сечение упругого рассеяния электронов на атоме, но с меньшей контрастностью из-за кратного рассеяния нек-рой части электронов (для Au~30%). Угл. распределение неупруго рассеянных электронов для лёгких веществ (Be, Al) - косинусоидальное при 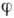=0 и сильно вытянуто в зеркальном направлении при =60-85° (малоугловое рассеяние). При 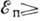1 кэВ для веществ со средними и большими Z наОлюдаются электроны рассеянные как на малые углы (при больших 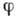), так и на углы ~180°.

T. к. неупругое отражение обусловлено упругим взаимодействием электронов с атомами твёрдого тела и их последующим торможением без существ. изменения направления движения (модель непрерывных потерь), то угл. распределение неупруго рассеянных электронов отражает особенности угл. распределения упруго отражённых.

Полной теории В. э. э. пока не существует. Отд. особенности В. э. э. описываются либо в рамках квантово-механич. приближения (упругое рассеяние электронов, возбуждение внутренних истинно вторичных электронов), либо в рамках кинетич. ур-ния Больцмана (транспорт внутренних истинно вторичных электронов и их размножение - каскадный процесс). Особенности В. э. э. монокристаллов объясняются с помощью теории дифракции электронов.

Применение. В. э. э. используется для усиления электронных потоков в эл.-вакуумных приборах (вторичные и фотоэлектронные умножители, усилители яркости изображения и т. д.), для записи информации в виде потенц. рельефа на поверхности диэлектрика (электронно-лучевые приборы). В. э. э. играет также важную роль в работе ряда высокочастотных приборов. В ряде случаев В. э. э.- "вредный" эффект, напр. при зарядке стекла и диэлектриков в эл.-вакуумных приборах.

Лит.: Добрецов Л. H., Гомоюновa M. В., Эмиссионная электроника, M., 1966; Бронштейн И. M., Фрайман Б. С., Вторичная электронная эмиссия, M., 1969; Афанасьев А. Г., Бронштейн И. M., Упругое отражение электронов и вторичная электронная эмиссия CsI при малых энергиях вторичных электронов, "Изв. АН СССР, сер. физ.", 1973, т. 37, № 12, с. 2492; их же. Распределение вторичных электронов по энергиям для CsI и KI, "ФТТ", 1976, т. 18, с. 1129; Шульман А. Р., Фридрихов С. А., Вторично-эмиссионные методы исследования твердого тела, M., 1977; Бронштейн И. M., Стожаров В. M., Новые данные об угловом и энергетическом распределении вторичных электронов, "Изв. АН СССР, сер. физ.", 1979, т. 43, JMi 3, с. 500; Кораблев В. В., Mайоров А. А., Анизотропия эмиссии вторичных и оже-электронов для монокристаллов со сниженной работой выхода, там же, с. 635 .

И. M. Бронштейн, В. В. Кораблев.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.