ДЕФОРМИРОВАННЫЕ ЯДРА

ДЕФОРМИРОВАННЫЕ ЯДРА

- атомные ядра, форма к-рых в основном состоянии отличается от сферической. Они имеют аномально большие электрич. квадрупольные моменты Q - в 30 раз больше предсказываемых одночастичной оболочечной моделью ядра. Д. я. были открыты в 1949 в результате измерения Q. Доказательством их существования являются спектры возбуждённых состояний Д. я., образующие систему вращат. полос (см. Вращательное движение ядра).

На каждом состоянии Д. я. основана вращат. полоса, уровни к-рой имеют определ. чётность и последовательность угл. моментов I. Для сферич. ядра коллективное вращение (согласно квантовой механике) невозможно. Коллективное вращение и движение нуклонов в Д. я. в нек-ром приближении можно считать независимыми (адиабатич. приближение).

В зависимости от числа нуклонов А (массового числа) существует 5 областей Д. я.: 1) лёгкие ядра с 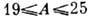(изотопы Mg и Al); 2) нейтроноизбыточные ядра с (изотопы Zr, Mo, Ru и Pd); 3) нейтронодефицитные ядра изотопов Xe и Ba с ; 4) ядра редкоземельных элементов с ; 5) ядра актинидов с 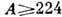, включая трансурановые элементы.

Деформация ядер - квантовый эффект, связанный с оболочечной структурой ядра. Конфигурации заполненных оболочек сферически симметричны. Напротив, орбиты частиц, не входящих в заполненные оболочки, анизотропны, что приводит к отклонению формы ядра от сферически симметричной. Все обнаруженные Д. я. имеют форму вытянутых эллипсоидов вращения. Отклонению от аксиальной симметрии препятствуют спинорбитальное взаимодействие нуклонов и парные корреляции нуклонов в ядре (см. ниже). Неаксиальная форма возможна у самых лёгких Д. я. Неск. нуклонов сверх заполненных оболочек в этих ядрах составляют значит. часть всех частиц в ядре, что приводит к наибольшим наблюдаемым деформациям.

Деформация ядер в возбуждённых состояниях менее изучена. Установлено, что величина Q в состояниях, соответствующих вращат. полосе, слабо изменяется с ростом полного угл. момента ядра I до 20. Оболочечные эффекты могут приводить к образованию возбуждённых конфигураций, форма к-рых существенно отличается от равновесной формы ядра в основном состоянии (изомеры формы). Наблюдаются высокоспиновые изомерные состояния сферич. ядер, в к-рых ядро имеет сплюснутую форму (сфероид); пример-деформированные возбуждённые состояния сферич. ядер ¹⁶O и ⁴⁰Ca с заполненными оболочками. В Д. я. 5-й области обнаружены спонтанно делящиеся изомеры формы (см. Деление ядер).

Рис. 1. Схема связи угловых моментов в медленно вращающемся деформированном ядре: R - угловой момент коллективного вращения,j -суммарный угловой момент нуклонов, I - полный угловой момент.

Электрические квадрупольные моменты и параметры квадрупольной деформации. Большой квадрупольный момент Q уядер, удалённых от магических ядер, обусловлен когерентным смешиванием нуклонных оболочечных конфигураций. Аксиальное ядро характеризуется внутр. электрич. квадрупольным моментом Q₀, т. е. квадрупольным моментом относительно собств. системы координат , жёстко связанной с ядром (рис. 1). Вращение ядра приводит к усреднению зарядового эксцентриситета. Статич. квадрупольный момент Q ядра определяется как ср. значение этой величины в состоянии с макс. проекцией (M=I )полного угл. момента I ядра на выделенное в пространстве направление z (рис. 1):

Здесь К - проекция / на ось z', совпадающую с осью симметрии Д. я. Для основного состояния ядра K=I, поэтому:

Из (2) видно, что в состояниях с I=0 и , даже если (согласно квантовой механике, направление оси симметрии ядра в пространстве в этом случае равновероятно). Величина Q определяется из сверхтонкой структуры атомных спектров, a Q₀ - из сечений кулоновского возбуждения вращат. состояний или их времён жизни (последние измерения дают величину , знак Q₀ устанавливается по Q; см. Кулоновское возбуждение ядра).

Рис. 2. Параметры b₂, квадрупольной деформации основных состояний ядер с А>150; - четно-чётные ядра, - нечётно-протонные ядра,- нечетно-нечётные ядра,- нечётно-нейтронные ядра.

Параметры деформации ядра определяются по величине Q₀ и зависят от распределения плотности ядерного вещества. В простейшем случае предполагается, что ядро - равномерно заряженный эллипсоид вращения с полуосями а>b. Плотность распределения нейтронов и протонов постоянна внутри эллипсоида и равна 0 вне его (модель ядра с резким краем). Размер ядра определяется среднеквадратичным радиусом Ферми, а его форма выражением:

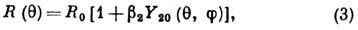
где 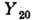- сферич. ф-ция, b₂ наз. параметром квадрупольной деформации:

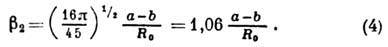
При малых деформациях:

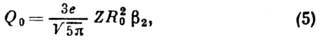
где е - элементарный заряд. Для больших деформаций в (5) следует заменить на

Для Д. я. 4-й и 5-й групп ~0,2- 0,3 (рис. 2), что согласуется с оценкой [отношение числа нуклонов вне заполненных оболочек к А]. Ядра с нечётным А и нечётно-нечётные ядра имеют примерно такую же равновесную деформацию, как и соседние четно-чётные ядра.

Др. определение параметра квадрупольной деформации :

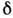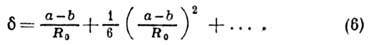
Для него Q₀ пропорц. при любой величине деформации. Соотношение между и 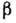имеет вид:

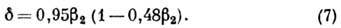
Деформации высших порядков. Кроме квадрупольной деформации, играющей гл. роль, Д. я. обладают аксиальными деформациями высш. порядков. Форма ядра, имеющего квадрупольную и гексадекапольную (4-го порядка) деформации, даётся выражением:

где 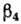- параметр гексадекапольной деформации (рис. 3). С учётом для ядра с резкой границей описывается ф-лой (5), в к-рой следует заменить на

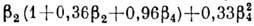
Параметр гексадекапольной деформации для редкоземельных ядер меньше 0 и в 20-30 раз меньше .

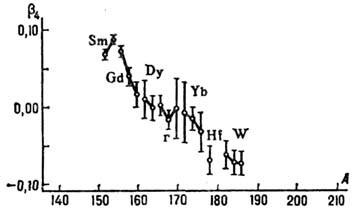
Рис. 3. Гексадекапольные деформации основных состояний ядер редкоземельных элементов; вертикальные линии - ошибки измерений.

Структура основных состояний. Д. я. обладают широким спектром коллективных и одночастичных движений, в к-рых проявляются как макроскопич. свойства ядра, так и оболочечные (квантовые) эффекты. Для описания одночастичного движения нуклонов в Д. я. используется несферич. ср. поле, представляющее собой аксиально-симметричный, квадрупольно-деформированный потенциал, учитывающий спин-орбитальное взаимодействие нуклонов. Наиб. распространён т. н. потенциал Нильссона - потенциал анизотропного гармонич. осциллятора. Потенциал Нильссона имеет бесконечную глубину, поэтому он плохо описывает движение нуклонов на границе и вне ядра. Ближе к реальному ср. полю ядра потенциал конечной глубины с размытым краем (потенциал Саксона - Вудса). Для нейтронной и протонной систем потенциалы поля несколько отличны.

Квантовые числа однонуклонного движения определяются симметрией ср. поля. Пространств. чётность и проекция полного угл. момента 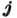нуклона на ось симметрии ядра 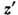являются интегралами движения. Состояние с данным двукратно вырождено, т. к. орбиты, отличающиеся только знаком , инвариантны относительно отражения времени. Следствием аксиальности деформации является равенство .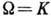

Для определения др. квантовых чисел Д. я. важна близость ср. поля ядра к потенциалу гармонич. осциллятора. В анизотропном осцилляторном потенциале движение разделяется на независимые колебания вдоль оси z' (квантовое число n_z') и в плоскости, перпендикулярной этой оси . Вырожденные состояния с одинаковым 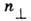можно характеризовать проекцией орбитального момента нуклона на ось :

Однако из-за спин-орбитальной связи ни , ни проекция спина нуклона на ось не сохраняются, сохраняется проекция полного угл. момента .

В реальном ядерном потенциале , n_z или N, n_z ( наз. гл. осцилляторным квантовым числом) приближённо сохраняются. Существование др. пары приближённых квантовых чисел не зависит от конкретного вида потенциала и является следствием аксиальной симметрии ядра (в несферич. потенциале состояния с различными 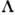, связанные спин-орбитальным взаимодействием, различаются по энергии и поэтому слабо смешиваются). Четыре приближённых квантовых числа полностью характеризуют состояние нуклона в ср. поле ядра. Для квантовых чисел однонуклонного движения принята запись:

причём .

В основном состоянии четно-чётных Д. я. уровни ср. поля нейтронов или протонов заполняются нуклонами попарно . Такое "выстраивание" орбитального движения нуклонов приводит к нулевой суммарной проекции угл. момента ядра / на ось симметрии z':

.

Последняя заполненная орбита в нейтронных или протонных конфигурациях наз. энергией или поверхностью Ферми (энергия Ферми нейтронов , протонов ). У Д. я. с нечётным числом нуклонов все низшие орбиты попарно заполнены, а нечётный нуклон занимает низший свободный уровень. Поэтому К и основного состояния нечётного ядра совпадают с орбиты нечётного нуклона. У нечётно-нечётных Д. я. нечётный нейтрон и протон находятся на двух разл. орбитах, если число нейтронов и протонов различно. Все низшие орбиты нейтронов и протонов попарно заполнены. В основном состоянии нейтрон и протон должны находиться в триплетном спиновом состоянии: (правило Галлахера - Moшневского), поэтому .

Возбуждённые состояния Д. я. Парные корреляции нуклонов. Возбуждённые состояния ядер образуются при переходе частиц из заполненных уровней на свободные. Незаполненные орбиты под уровнем Ферми образуют "дырочные" состояния, а заполненные над уровнем Ферми - "частичные". Возбуждённые состояния определяются гл. обр. т. н. остаточным взаимодействием между нуклонами, в частности взаимодействием, переводящим пару нуклонов одного сорта из состояния в состояние , где - совокупности квантовых чисел (10), а - сопряжённые по времени состояния с проекцией момента -. Это взаимодействие приводит к парным корреляциям сверхпроводящего типа, к-рые в Д. я. характеризуются сильным конфигурационным смешиванием уровней и находящихся в интервале энергий порядка энергии корреляции пары по обе стороны от поверхности Ферми.

Парные корреляции в Д. я. существуют независимо в протонной и нейтронной системах (нейтрон - протонное спаривание не играет роли). Пара образована нуклонами с противоположным знаком . Число коррелированных пар , где - плотность одночастичных уровней у поверхности Ферми. Энергия корреляции для протонов несколько больше, чем для нейтронов. В среднем для четно-чётных Д. я. редкоземельных элементов =0,8 МэВ, =0,9 МэВ; для актинидов - =0,7 МэВ, 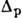=0,8 МэВ.

Несмотря на сильное конфигурационное смешивание, одночастичное движение нуклонов сохраняет характерные черты, в частности сохраняются К и основных состояний ядер. Однако в результате когерентного взаимодействия, в к-ром участвуют частиц вблизи поверхности Ферми, в ядре возникают элементарные возбуждения, наз. квазичастицами. Квазичастица представляет собой суперпозицию частицы и дырки. Основным состоянием четно-чётного ядра является вакуум квазичастиц, а возбуждённые ядра содержат чётное число квазичастиц. В этих ядрах нет квазичастичных возбуждений с энергией <1,5-2,0 МэВ, т. к. мин. энергия двухквазичастичного возбуждения, связанного с разрывом пары, равна . Энергетич. щель в спектре возбуждённых состояний четно-чётных Д. я.- характерный признак парных корреляций сверхпроводящего типа.

В основном состоянии нечётных Д. я. неспаренный нуклон занимает уровни, ближайшие к поверхности Ферми, уменьшая тем самым объём фазового пространства для взаимодействия остальных нуклонов того же сорта. Этот т. н. эффект блокировки уменьшает приблизительно на 10-20% по сравнению с чётными Д. я. Возбуждённые уровни нечётных Д. я. с энергией <0,5 МэВ - одноквазичастичные состояния нечётного нуклона. Плотность уровней в этом интервале энергий примерно вдвое превышает плотность одночастичных состояний ср. поля ядра, что объясняется характерным спектром одноквазичастичных возбуждений:

где - энергия нуклона в ср. поле в состоянии с квантовыми числами . При 1,5-2,0 МэВ плотность уровней сильно возрастает из-за появления трёхквазичастичных возбуждений. В интервале МэВ плотность возбуждённых уровней также больше одно-квазичастичной из-за состояний, представляющих собой суперпозицию одноквазичастичных возбуждений с колебательными (см. Колебательные возбуждения ядер).

Магнитный момент Д. я. обусловлен вращением ядра как целого и внутр. движением нуклонов. Его можно представить в виде:

Здесь 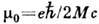- ядерный магнетон (M - масса нуклона), g_R - коллективное гиромагнитное отношение, g_k - внутр. g-фактор, - вращат. момент ядра (рис. 1). В состояниях вращат. полосы с K=0 четно-чётных Д. я. магн. момент определяется только коллективным вращением:

В полосах четно-чётных ядер с и нечётных с :

Магн. момент состояний нечётных ядер с зависит также от т. н. магн. параметра развязывания, к-рый определяется внутр. структурой ядра.

Коллективное гиромагн. отношение g_R определяется относит. вкладом протонов во вращат. движение ядра. Оно равно отношению момента инерции протонов J_P к полному моменту инерции ядра :

Величина g_R в ср. на 20% меньше значения Z/A, получающегося для равномерно заряженного вращающегося твёрдого ядра. В нечётном ядре нечётный нуклон увеличивает либо J_P для нечётно-протонных ядер, либо J _п для нечётно-нейтронных и коллективный g-фактор первых больше, а вторых меньше, чем g_R для соседних четно-чётных ядер. По абс. величине эта четно-нечётная разность коллективных гиромагнитных отношений 30%.

Лит.: Рейнуотер Д ж., Как возникла модель сфероидальных ядер, пер. с англ., "УФН", 1976, т. 120, с. 529; Бор О., Моттельсон Б., Структура атомного ядра, пер. с англ., т. 2, M., 1977, гл. 4,5. И. M. Павличенков.

Динамика дефектов. Точечные дефекты типа примесей, вакансий или междоузельных атомов способны перемещаться в кристалле путём диффузии. Но классич. диффузию нельзя считать динамич. процессом, т. к. очередной скачок дефекта имеет случайное направление и только усреднение по большому числу дефектов может дать нек-рую направленность их движению. Иначе могут вести себя точечные дефекты в квантовом кристалле, когда для дефекта появляется возможность перехода из одного положения в соседнее путём квантового туннелирования (см. Туннельный эффект). В результате дефект может превратиться в квазичастицу - дефектон, свободно перемещающуюся в кристалле.

Междоузельный атом приобретает способность к механич. перемещению в т. н. краудионной конфигурации даже в классич. кристалле (см. Краудион)."Лишний" атом оказывается как бы распределённым между неск. узлами плотно упакованного атомного ряда и потому легко перемещается вдоль этого направления.

Чисто механич, перемещение (скольжение) характерно для специфического линейного дефекта - дислокации. Смещение её линии по плоскости скольжения не нарушает сплошности кристалла, а потому происходит сравнительно легко. Движение дислокации всегда связано с неупругим изменением формы кристаллич. образца, поэтому дислокация является элементарным носителем пластичности кристалла. Атомная перестройка, сопровождающая перемещение дислокации, требует не очень больших нагрузок, и в этом причина того, что пластич. деформация кристалла начинается при напряжениях, малых по сравнению с теоретич. прочностью кристалла.

Нестационарное движение дислокации (с ускорением) сопровождается изучением упругих (звуковых) волн, подобно тому как нестационарное движение электрич. зарядов приводит к излучению эл.-магн. волн. С др. стороны, взаимодействуя с интенсивными колебаниями кристалла, дислокация вовлекается в осцилляторное диссипативное движение и даёт важный вклад во внутреннее трение.

Двухмерные дефекты типа двойников (см. Двойникование), трещин или мартенситных включений также могут проявлять себя как динамич. образования. Наряду с дислокациями они играют определяющую роль в пластичности и прочности кристаллов.

Взаимодействие с проникающим излучением. Динамич. взаимодействие кристалла с фотонами разной энергии (в т. ч. рентгеновскими и -квантами), нейтронами или ускоренными заряж. частицами имеет разное проявление в зависимости от энергии и импульса, передаваемых кристаллу дроникающей частицей. Если эта энергия сравнима с , а передаваемый импульс имеет порядок величины , то происходит неупругий процесс рассеяния частицы, сопровождающийся рождением одного или неск. фононов. Изучение таких процессов позволяет определить закон дисперсии колеблющегося кристалла (рис. 2). Однако возможен процесс без отдачи, при к-ром энергия частицы сохраняется и в кристалле не происходит рождения фонона. Такие процессы (типа Мёссбауэра эффекта )характеризуются предельно узкими дифракционными линиями, и их доля измеряется Дебая - Уоллера фактором.

Если кинетич. энергия частицы велика, то она способна выбить атомы кристалла из равновесных положений, сообщая им значит. энергию и превращая их в движущиеся дефекты. Они, в свою очередь, создают вторичные смещения атомов и смещения более высоких порядков, в результате чего возникает каскад точечных дефектов. Однако существуют такие направления, параллельные атомным рядам и атомным плоскостям ("каналы"), вдоль к-рых быстрые заряж. частицы с длиной волны де Бройля, значительно меньшей а, движутся, практически не вызывая смещения атомов. Явление каналирования частиц различно для частиц разного знака зарядов (электронов и позитронов и т. п.).

Лит.: Борн M., Хуан Кунь, Динамическая теория кристаллических решеток, пер. с англ., M., 1958; Косевич A. M., Физическая механика реальных кристаллов, К., 1981; Lifshitz I. M., Kosevich A.M., The dynamics of a crystal lattice with defects, "Kept. Progr. Phys.", 1966, v. 29, pt 1, p. 217. A. M. Косевич.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.