ВИНЕРА-ХИНЧИНА ТЕОРЕМА

-утверждение о том, что спектральная плотность 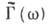стационарного случайного процесса 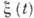, связанная с его корреляц. ф-цией 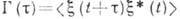преобразованием Фурье:

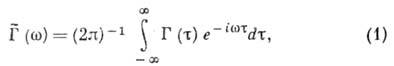
неотрицательна, 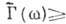О (угловые скобки означают статистич. усреднение, * - комплексное сопряжение). Спектральную плотность наз. также спектром мощности случайного процесса. В.-X. т. получена H. Винером (N. Wiener) в 1930, в иной формулировке - А. Я. Хинчиным в 1934.

Неотрицательность спектральной плотности 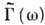позволяет трактовать эту величину (при 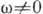) как меру интенсивности флуктуации случайного процесса 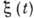на частоте 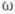. Такая трактовка становится очевидной, если заметить, что спектральная плотность связана со случайным спектром

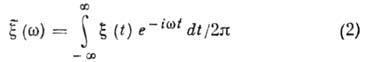
соотношением 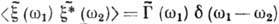, где 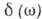- дельта-функция. Это наглядное соотношение непосредственно вытекает из (1) и (2) и при теоретич. анализе обычно позволяет получать правильные следствия, однако оно является чисто формальным, т. к. отд. реализации стационарного процесса , вообще говоря, не исчезают при и спектр (2) в обычном смысле не существует. Чтобы обойти эту трудность, достаточно рассмотреть вместо (2) спектр "обрезанных" реализаций:

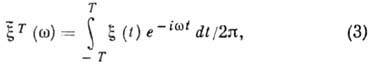
к-рый при больших T можно трактовать как нек-рую аппроксимацию (2). Из (1) и (3) следует, что для стационарного 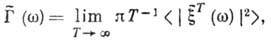процесса т. е. спектральная плотность пропорциональна ср. квадрату амплитуды случайного спектра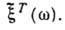

Спектральная плотность 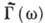служит одним из осн. понятий при корреляц. анализе случайных ф-ций в статистич. радиофизике, в теории равновесных тепловых флуктуации, в физ. кинетике и др. и допускает непо-средств. обобщение на статистически однородные и стационарные случайные поля, переходя в пространственно-временной спектр случайного поля.

Лит.: Гроот С. де, Мазур П., Неравновесная термодинамика, пер. с англ., M., 1964; Введение в статистическую радиофизику, ч. 1 - Рытов С. M., Случайные процессы, M., 1976; ч. 2 - Рытов С. M., Кравцов Ю. А., Татарский В. И., Случайные поля, M., 1978; Яглом A. M., Корреляционная теория стационарных случайных функций с примерами из метеорологии, Л., 1981. Л. Л. Апресян.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.

Игры ⚽ Поможем сделать НИР

Полезное

Смотреть что такое "ВИНЕРА-ХИНЧИНА ТЕОРЕМА" в других словарях:

Теорема Хинчина-Колмогорова — (также известная как Теорема Винера Хинчина и иногда как Теорема Винера Хинчина Эйнштейна) утверждает, что спектральной плотностью мощности стационарного в широком смысле случайного процесса является преобразование Фурье соответствующей… … Википедия
Теорема Хинчина — Теорема Хинчина Колмогорова (также известная как Теорема Винера Хинчина и иногда как Теорема Винера Хинчина Эйнштейна) утверждает, что спектральной плотностью мощности стационарного в широком смысле случайного процесса… … Википедия
СЛУЧАЙНЫЙ ПРОЦЕСС — ф ция непрерывного времени ,значение к рой в каждый момент является случайной величиной, т … Физическая энциклопедия
КОРРЕЛЯЦИОННАЯ ТЕОРИЯ — случайных функций описание случайных ф ций при помощи статистич. моментов 1 го и 2 го порядка: . Аргумент случайной ф ции x может иметь любую размерность. Если гауссова случайная ф ция, полностью определяемая первым и вторым моментами, то К. т.… … Физическая энциклопедия
КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ — случайного процесса ф ция В (s, t) = М[ Х (s) MX (s)].[X(t) MX (t)]*, s, , [здесь MX (t) первый момент процесса, * означает комплексное сопряжение; предполагается, что . В случае векторного процесса К. ф. наз коррел … Физическая энциклопедия
Винер, Норберт — Норберт Винер англ. Norbert Wiener … Википедия
Спектральная плотность — В статистической радиотехнике и физике при изучении детерминированных сигналов и случайных процессов широко используется их спектральное представление в виде спектральной плотности, которая базируется на преобразовании Фурье. Если процесс имеет… … Википедия
Интерполяционная формула Уиттакера-Шеннона — служит для восстановления непрерывного сигнала с ограниченным спектром из последовательности равноотстоящих отсчетов. Интерполяционная формула, как ее обычно называют, восходит к работе Эмиля Бореля датированной 1898 годом, и к работе… … Википедия
Интерполяционная формула Уиттекера-Шеннона — служит для восстановления непрерывного сигнала с ограниченным спектром из последовательности равноотстоящих отсчётов. Интерполяционная формула, как её обычно называют, восходит к работе Эмиля Бореля датированной 1898 годом, и к работе Эдмунда… … Википедия
Интерполяционная формула Уиттекера — Шеннона служит для восстановления непрерывного сигнала с ограниченным спектром из последовательности равноотстоящих отсчётов. Интерполяционная формула, как её обычно называют, восходит к работе Эмиля Бореля, датированной 1898 годом, и к работе… … Википедия

Словари и энциклопедии на Академике

ВИНЕРА-ХИНЧИНА ТЕОРЕМА

Полезное

Смотреть что такое "ВИНЕРА-ХИНЧИНА ТЕОРЕМА" в других словарях:

Поделиться ссылкой на выделенное

Словари и энциклопедии на Академике

Физическая энциклопедия

ВИНЕРА-ХИНЧИНА ТЕОРЕМА

Полезное

Смотреть что такое "ВИНЕРА-ХИНЧИНА ТЕОРЕМА" в других словарях:

Поделиться ссылкой на выделенное

Прямая ссылка: