- МАКСВЕЛЛА УРАВНЕНИЯ
- МАКСВЕЛЛА УРАВНЕНИЯ
-
фундаментальные ур-ния классич. макроскопич. электродинамики, описывающие эл.-магн. явления в любой среде (и в вакууме). Сформулированы в 60-х гг. 19 в. Дж. Максвеллом на основе обобщения эмпирич. законов электрич. и магн. явлений и развития идеи англ. учёного М. Фарадея о том, что вз-ствия между электрически заряж. телами осуществляются посредством эл.-магн. поля. Совр. форма М. у. дана нем. физиком Г. Герцем и англ. физиком О. Хевисайдом.М. у. связывают величины, характеризующие эл.-магн. поле, с его источниками, т. е. с распределением в пр-ве электрич. зарядов и токов. В вакууме эл.-магн. поле характеризуется напряжённостью электрич. поля Е и магн. индукцией В — векторными величинами, зависящими от пространств. координат и времени. Эти величины определяют силы, действующие со стороны поля на заряды и токи, распределение к-рых в пр-ве задаётся плотностью заряда r (величиной заряда в ед. объёма) и плотностью электрического тока j. Для описания эл.-магн. процессов в матер. среде, кроме Е и В, вводятся вспомогат. векторные величины, зависящие от состояния и св-в среды: электрич. индукция D и напряжённость магн. поля Н.М. у. позволяют определить осн. хар-ки поля (E, В, D и Н) в каждой точке пр-ва в любой момент времени, если известны источники поля j и r как ф-ции координат и времени. М. у. могут быть записаны в интегр. или дифф. форме (ниже они приводятся в Гаусса системе единиц).М. у. в и н т е г р а л ь н о й ф о р м е определяют не векторы E, В, D и Н в отд. точках пр-ва, а нек-рые интегр. величины, зависящие от распределения этих хар-к поля: циркуляцию векторов Е и Н вдоль произвольных замкнутых контуров и потоки векторов D и B через произвольные замкнутые поверхности.Первое М. у. явл. обобщением на перем. поля эмпирического Био — Савара закона о возбуждении магн. поля электрич. токами. Максвелл высказал гипотезу, что магн. поле порождается не только токами, текущими в проводнике, но и перем. электрич. полями в диэлектриках или вакууме. Величина, пропорц. скорости изменения электрич. поля во времени, была названа Максвеллом током смещения, он возбуждает магн. поле по тому же закону, что и ток проводимости. Полный ток, равный сумме тока смещения и тока проводимости, всегда явл. замкнутым. Первое М. у. имеет вид: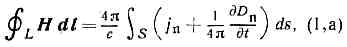 т. е. циркуляция вектора магн. напряжённости вдоль замкнутого контура L (сумма скалярных произведений вектора Н в данной точке контура на бесконечно малый отрезок dl контура) определяется полным током через произвольную поверхность S, ограниченную данным контуром. Здесь jn — проекции плотности тока проводимости j на нормаль к бесконечно малой площадке ds, являющейся частью поверхности S; (1/4p)(дDn/дt) — проекция плотности тока смещения на ту же нормаль; с—3•1010см/с — постоянная, равная скорости распространения эл.-магн. вз-ствий (скорость света) в вакууме.Второе М. у. является матем. формулировкой закона электромагнитной индукции Фарадея и записывается в виде:
т. е. циркуляция вектора магн. напряжённости вдоль замкнутого контура L (сумма скалярных произведений вектора Н в данной точке контура на бесконечно малый отрезок dl контура) определяется полным током через произвольную поверхность S, ограниченную данным контуром. Здесь jn — проекции плотности тока проводимости j на нормаль к бесконечно малой площадке ds, являющейся частью поверхности S; (1/4p)(дDn/дt) — проекция плотности тока смещения на ту же нормаль; с—3•1010см/с — постоянная, равная скорости распространения эл.-магн. вз-ствий (скорость света) в вакууме.Второе М. у. является матем. формулировкой закона электромагнитной индукции Фарадея и записывается в виде: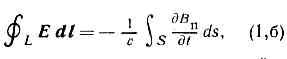 т. е. циркуляция вектора напряженности электрич. поля вдоль замкнутого контура L (эдс индукции) определяется скоростью изменения потока вектора магн. индукции через поверхность S, ограниченную данным контуром. Здесь Bn — проекция на нормаль к площадке ds вектора магн. индукции В; знак «-» соответствует Ленца правилу для направления индукц. тока.Третье М. у. выражает опытные данные об отсутствии магн. зарядов, аналогичных электрическим (магн. поле порождается только электрич. токами):
т. е. циркуляция вектора напряженности электрич. поля вдоль замкнутого контура L (эдс индукции) определяется скоростью изменения потока вектора магн. индукции через поверхность S, ограниченную данным контуром. Здесь Bn — проекция на нормаль к площадке ds вектора магн. индукции В; знак «-» соответствует Ленца правилу для направления индукц. тока.Третье М. у. выражает опытные данные об отсутствии магн. зарядов, аналогичных электрическим (магн. поле порождается только электрич. токами):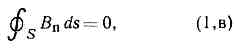 т. е. поток вектора магн. индукции через произвольную замкнутую поверхность S равен нулю.Четвёртое М. у. (обычно наз. Гаусса теоремой) представляет собой обобщение закона вз-ствия неподвижных электрич. зарядов — Кулона закона:
т. е. поток вектора магн. индукции через произвольную замкнутую поверхность S равен нулю.Четвёртое М. у. (обычно наз. Гаусса теоремой) представляет собой обобщение закона вз-ствия неподвижных электрич. зарядов — Кулона закона: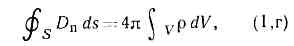 т. е. поток вектора электрич. индукции через произвольную замкнутую поверхность S определяется электрич. зарядом, находящимся внутри этой поверхности (в объёме V, ограниченном поверхностью S).Если считать, что векторы эл.-магн. поля (Е, В, D и Н) явл. непрерывными ф-циями координат, то, рассматривая циркуляцию Н и Е по бесконечно малым контурам и потоки векторов В и D через поверхности, ограничивающие бесконечно малые объёмы, можно от интегральных М. у- (1, а—г) перейти к системе дифференциальных М. у., характеризующих поле в каждой точке пр-ва:
т. е. поток вектора электрич. индукции через произвольную замкнутую поверхность S определяется электрич. зарядом, находящимся внутри этой поверхности (в объёме V, ограниченном поверхностью S).Если считать, что векторы эл.-магн. поля (Е, В, D и Н) явл. непрерывными ф-циями координат, то, рассматривая циркуляцию Н и Е по бесконечно малым контурам и потоки векторов В и D через поверхности, ограничивающие бесконечно малые объёмы, можно от интегральных М. у- (1, а—г) перейти к системе дифференциальных М. у., характеризующих поле в каждой точке пр-ва: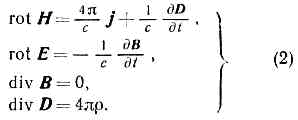 Физ. смысл ур-ний (2) тот же, что ур-ний (1).М. у. в форме (1) или (2) не образуют полной замкнутой системы, позволяющей рассчитывать эл.-магн. процессы при наличии матер. среды. Их необходимо дополнить соотношениями, связывающими векторы Е, Н, D, В и j, к-рые не являются независимыми. Связь между ними определяется св-вами среды и её состоянием, причём D и 3 выражаются через Е, а В — через Н:D=D(E), B=B(H),j=j(E). (3)Эти ур-ния наз. ур-ниями состояния или материальными ур-ниями; они описывают эл.-магн. св-ва среды и для каждой конкретной среды имеют определ. форму. В вакууме D?Е и В?Н.Совокупность ур-ний поля (2) и ур-ний состояния (3) образуют полную систему ур-ний.Макроскопич. М. у. описывают среду феноменологически, не рассматривая сложного механизма вз-ствия эл.-магн. поля с заряж. ч-цами среды. М. у. могут быть получены из Лоренца — Максвелла уравнений для микроскопич. полей и определ. представлений о строении в-ва путём усреднения микрополей по малым пространственно-временным интервалам. Таким способом получаются как осн. ур-ния поля (2), так и конкретная форма ур-ний состояния (3), причём вид ур-ний поля не зависит от св-в среды.Ур-ния состояния в общем случае очень сложны, т. к. векторы D, В и j в данной точке пр-ва в данный момент времени могут зависеть от полей E и H и If во всех точках среды во все предшествующие моменты времени. В нек-рых средах векторы D и В могут быть отличными от нуля при Е и Н равных нулю (сегнетоэлектрики и ферромагнетики). Однако для большинства изотропных сред, вплоть до весьма значит. полей, ур-ния состояния имеют простую линейную форму:D=eE, B=mH, j=sE+jстр. (4)Здесь e(х, у, z) — диэлектрическая проницаемость, a m(х, у, z) — магнитная проницаемость среды (для вакуума в системе СГС e=m=1), величина s(х, у, z) наз. удельной электропроводностью, j'стр — плотность т. н. сторонних токов, т. е. токов, поддерживаемых любыми силами, кроме см электрич. поля (напр., маги. полем, диффузией). В феноменологич. теории Максвелла макроскопич. характеристики эл.-магн. св-в среды e, m и s должны быть найдены экспериментально. В микроскопич. теории Лоренца — Максвелла они могут быть рассчитаны.Проницаемости e и m фактически определяют тот вклад в эл.-магн. поле, к-рый вносят т. н. связанные заряды, входящие в состав электрически нейтр. атомов и молекул в-ва. При известных из опыта e, m и s можно рассчитать эл.-магн. поле в среде, не решая трудную вспомогат. задачу о распределении связанных зарядов и соответствующих им токов в в-ве. Плотность заряда r и плотность тока j в М. у.— это плотности свободных зарядов и токов, причём вспомогат. векторы Н и D вводятся так, чтобы циркуляция вектора Н определялась только движением свободных зарядов, а поток вектора D — плотностью распределения этих зарядов в пр-ве.Если эл.-магн. поле рассматривается в двух граничащих средах, то на поверхности раздела векторы поля могут претерпевать разрывы (скачки); в этом случае ур-ния (2) должны быть дополнены граничными условиями:
Физ. смысл ур-ний (2) тот же, что ур-ний (1).М. у. в форме (1) или (2) не образуют полной замкнутой системы, позволяющей рассчитывать эл.-магн. процессы при наличии матер. среды. Их необходимо дополнить соотношениями, связывающими векторы Е, Н, D, В и j, к-рые не являются независимыми. Связь между ними определяется св-вами среды и её состоянием, причём D и 3 выражаются через Е, а В — через Н:D=D(E), B=B(H),j=j(E). (3)Эти ур-ния наз. ур-ниями состояния или материальными ур-ниями; они описывают эл.-магн. св-ва среды и для каждой конкретной среды имеют определ. форму. В вакууме D?Е и В?Н.Совокупность ур-ний поля (2) и ур-ний состояния (3) образуют полную систему ур-ний.Макроскопич. М. у. описывают среду феноменологически, не рассматривая сложного механизма вз-ствия эл.-магн. поля с заряж. ч-цами среды. М. у. могут быть получены из Лоренца — Максвелла уравнений для микроскопич. полей и определ. представлений о строении в-ва путём усреднения микрополей по малым пространственно-временным интервалам. Таким способом получаются как осн. ур-ния поля (2), так и конкретная форма ур-ний состояния (3), причём вид ур-ний поля не зависит от св-в среды.Ур-ния состояния в общем случае очень сложны, т. к. векторы D, В и j в данной точке пр-ва в данный момент времени могут зависеть от полей E и H и If во всех точках среды во все предшествующие моменты времени. В нек-рых средах векторы D и В могут быть отличными от нуля при Е и Н равных нулю (сегнетоэлектрики и ферромагнетики). Однако для большинства изотропных сред, вплоть до весьма значит. полей, ур-ния состояния имеют простую линейную форму:D=eE, B=mH, j=sE+jстр. (4)Здесь e(х, у, z) — диэлектрическая проницаемость, a m(х, у, z) — магнитная проницаемость среды (для вакуума в системе СГС e=m=1), величина s(х, у, z) наз. удельной электропроводностью, j'стр — плотность т. н. сторонних токов, т. е. токов, поддерживаемых любыми силами, кроме см электрич. поля (напр., маги. полем, диффузией). В феноменологич. теории Максвелла макроскопич. характеристики эл.-магн. св-в среды e, m и s должны быть найдены экспериментально. В микроскопич. теории Лоренца — Максвелла они могут быть рассчитаны.Проницаемости e и m фактически определяют тот вклад в эл.-магн. поле, к-рый вносят т. н. связанные заряды, входящие в состав электрически нейтр. атомов и молекул в-ва. При известных из опыта e, m и s можно рассчитать эл.-магн. поле в среде, не решая трудную вспомогат. задачу о распределении связанных зарядов и соответствующих им токов в в-ве. Плотность заряда r и плотность тока j в М. у.— это плотности свободных зарядов и токов, причём вспомогат. векторы Н и D вводятся так, чтобы циркуляция вектора Н определялась только движением свободных зарядов, а поток вектора D — плотностью распределения этих зарядов в пр-ве.Если эл.-магн. поле рассматривается в двух граничащих средах, то на поверхности раздела векторы поля могут претерпевать разрывы (скачки); в этом случае ур-ния (2) должны быть дополнены граничными условиями: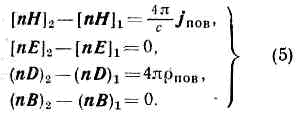 Здесь jпов и rпов — плотности поверхностных тока и заряда, квадратные и круглые скобки — соотв. векторные и скалярные произведения векторов, n — единичный вектор нормали к поверхности раздела и направления от первой среды ко второй (1®2), а индексы относятся к разным сторонам границы раздела.Осн. ур-ния для поля (2) линейны, ур-ния же состояния (3) в общем случае нелинейны. Обычно нелинейные эффекты обнаруживаются в достаточно сильных полях. В линейных средах (удовлетворяющих соотношениям (4)), и в частности в вакууме, М. у. линейны, так что для них справедлив суперпозиции принцип: при наложении полей они не оказывают влияния друг на друга.Из М. у. вытекает ряд законов сохранения. В частности, из ур-ний (1, а) и (1, г) можно получить т. н. ур-ние непрерывности:
Здесь jпов и rпов — плотности поверхностных тока и заряда, квадратные и круглые скобки — соотв. векторные и скалярные произведения векторов, n — единичный вектор нормали к поверхности раздела и направления от первой среды ко второй (1®2), а индексы относятся к разным сторонам границы раздела.Осн. ур-ния для поля (2) линейны, ур-ния же состояния (3) в общем случае нелинейны. Обычно нелинейные эффекты обнаруживаются в достаточно сильных полях. В линейных средах (удовлетворяющих соотношениям (4)), и в частности в вакууме, М. у. линейны, так что для них справедлив суперпозиции принцип: при наложении полей они не оказывают влияния друг на друга.Из М. у. вытекает ряд законов сохранения. В частности, из ур-ний (1, а) и (1, г) можно получить т. н. ур-ние непрерывности: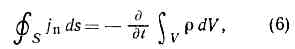 представляющее собой закон сохранения электрич. заряда: полный ток, протекающий за ед. времени через любую замкнутую поверхность S, равен изменению заряда внутри объёма V, ограниченного поверхностью S. Если ток через поверхность отсутствует, то заряд в объёме V остаётся неизменным.Из М. у. следует, что эл.-магн. поле обладает энергией и импульсом. Плотность энергии W (энергия поля в ед. объёма) равна:
представляющее собой закон сохранения электрич. заряда: полный ток, протекающий за ед. времени через любую замкнутую поверхность S, равен изменению заряда внутри объёма V, ограниченного поверхностью S. Если ток через поверхность отсутствует, то заряд в объёме V остаётся неизменным.Из М. у. следует, что эл.-магн. поле обладает энергией и импульсом. Плотность энергии W (энергия поля в ед. объёма) равна: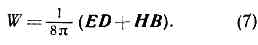 Эл.-магн. энергия может перемещаться в пр-ве. Плотность потока энергии определяется т. н. вектором Пойнтинга
Эл.-магн. энергия может перемещаться в пр-ве. Плотность потока энергии определяется т. н. вектором Пойнтинга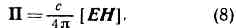 Направление вектора Пойнтинга перпендикулярно и E и H и совпадает с направлением распространения эл.-магн. энергии, а его величина равна энергии, переносимой в ед. времени через единичную поверхность, перпендикулярную П. Если эл.-магн. энергия не переходит в др. формы энергии, то, согласно М. у., изменение энергии в нек-ром объёме за ед. времени равно потоку эл.-магн. энергии через поверхность, ограничивающую этот объём. Если внутри объёма за счёт эл.-магн. энергии выделяется теплота, то закон сохранения энергии записывается в виде:
Направление вектора Пойнтинга перпендикулярно и E и H и совпадает с направлением распространения эл.-магн. энергии, а его величина равна энергии, переносимой в ед. времени через единичную поверхность, перпендикулярную П. Если эл.-магн. энергия не переходит в др. формы энергии, то, согласно М. у., изменение энергии в нек-ром объёме за ед. времени равно потоку эл.-магн. энергии через поверхность, ограничивающую этот объём. Если внутри объёма за счёт эл.-магн. энергии выделяется теплота, то закон сохранения энергии записывается в виде: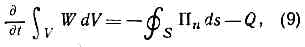 где Q — кол-во теплоты, выделяемой в ед. времени, Пn — проекция П на нормаль к бесконечно малой площадке ds.Плотность импульса эл.-магн. поля g (импульс ед. объёма поля) связана с плотностью потока энергии соотношением:
где Q — кол-во теплоты, выделяемой в ед. времени, Пn — проекция П на нормаль к бесконечно малой площадке ds.Плотность импульса эл.-магн. поля g (импульс ед. объёма поля) связана с плотностью потока энергии соотношением: Существование импульса эл.-магн. поля впервые было экспериментально обнаружено в опытах П. Н. Лебедева по измерению давления света (1899—1901).Как видно из (7), (8) и (10), эл.-магн. поле всегда обладает энергией, а поток энергии и эл.-магн. импульс отличны от нуля лишь в случае, когда одновременно существуют и электрич. и магн. поля, причём Е и Н не параллельны друг другу.М. у. приводят к фундам. выводу о конечности скорости распространения эл.-магн. вз-ствий. Это означает, что при изменении плотности заряда или тока, порождающих эл.-магн. поле, в нек-рой точке пр-ва на расстоянии R от них поле изменится спустя время t=R/c. Вследствие конечной скорости распространения эл.-магн. вз-ствий возможно существование электромагнитных волн, частным случаем к-рых (как впервые показал Максвелл) явл. световые волны.Эл.-магн. явления протекают одинаково во всех инерциальных системах отсчёта, т. е. удовлетворяют относительности принципу. В соответствии с этим М. у. не меняют своей формы при переходе от одной инерц. системы отсчёта к другой (релятивистски инвариантны). Выполнение принципа относительности для эл.-магн. процессов оказалось несовместимым с классич. представлениями о пр-ве и времени, потребовало пересмотра этих представлений и привело к созданию спец. относительности теории (А. Эйнштейн, 1905). Форма М. у. остаётся неизменной при переходе к новой инерц. системе отсчёта, если пространств. координаты и время, векторы поля E, Н, В и D, плотность тока j и плотность заряда r изменяются в соответствии с Лоренца преобразованиями. Релятивистски инвариантная форма М. у. подчёркивает тот факт, что электрич. и магн. поля образуют единое целое.М. у. описывают огромную область явлений. Они лежат в основе электротехники и радиотехники и играют важную роль в развитии таких актуальных направлений совр. физики, как физика плазмы и проблема управляемого термоядерного синтеза, магнитная гидродинамика, нелинейная оптика, конструирование ускорителей заряженных частиц, астрофизика и т. д. М. у. неприменимы лишь при больших частотах эл.-магн. волн, когда становятся существенными квант. эффекты, т. е. когда энергия отд. квантов эл.-магн. ноля — фотонов — велика и в процессах участвует сравнительно небольшое число фотонов.
Существование импульса эл.-магн. поля впервые было экспериментально обнаружено в опытах П. Н. Лебедева по измерению давления света (1899—1901).Как видно из (7), (8) и (10), эл.-магн. поле всегда обладает энергией, а поток энергии и эл.-магн. импульс отличны от нуля лишь в случае, когда одновременно существуют и электрич. и магн. поля, причём Е и Н не параллельны друг другу.М. у. приводят к фундам. выводу о конечности скорости распространения эл.-магн. вз-ствий. Это означает, что при изменении плотности заряда или тока, порождающих эл.-магн. поле, в нек-рой точке пр-ва на расстоянии R от них поле изменится спустя время t=R/c. Вследствие конечной скорости распространения эл.-магн. вз-ствий возможно существование электромагнитных волн, частным случаем к-рых (как впервые показал Максвелл) явл. световые волны.Эл.-магн. явления протекают одинаково во всех инерциальных системах отсчёта, т. е. удовлетворяют относительности принципу. В соответствии с этим М. у. не меняют своей формы при переходе от одной инерц. системы отсчёта к другой (релятивистски инвариантны). Выполнение принципа относительности для эл.-магн. процессов оказалось несовместимым с классич. представлениями о пр-ве и времени, потребовало пересмотра этих представлений и привело к созданию спец. относительности теории (А. Эйнштейн, 1905). Форма М. у. остаётся неизменной при переходе к новой инерц. системе отсчёта, если пространств. координаты и время, векторы поля E, Н, В и D, плотность тока j и плотность заряда r изменяются в соответствии с Лоренца преобразованиями. Релятивистски инвариантная форма М. у. подчёркивает тот факт, что электрич. и магн. поля образуют единое целое.М. у. описывают огромную область явлений. Они лежат в основе электротехники и радиотехники и играют важную роль в развитии таких актуальных направлений совр. физики, как физика плазмы и проблема управляемого термоядерного синтеза, магнитная гидродинамика, нелинейная оптика, конструирование ускорителей заряженных частиц, астрофизика и т. д. М. у. неприменимы лишь при больших частотах эл.-магн. волн, когда становятся существенными квант. эффекты, т. е. когда энергия отд. квантов эл.-магн. ноля — фотонов — велика и в процессах участвует сравнительно небольшое число фотонов.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- МАКСВЕЛЛА УРАВНЕНИЯ
-
Содержание:
1. Краткая история
2. Каноническая форма
3. Максвелла уравнения в интегральной форме
4. Общая характеристика Максвелла уравнений
5. Максвелла уравнения для комплексных амплитуд
6. Алгебраические Максвелла уравнения
7. Материальные уравнения
8. Граничные условия
9. Двойственная симметрия Максвелла уравнений
10. Максвелла уравнения в четырёхмерном представлении
11. Лоренц-инвариантность Максвелла уравнений
12. Лагранжиан для электромагнитного поля
13. Единственность решений Максвелла уравнений
14. Классификация приближений Максвелла уравнений
15. Максвелла уравнения в различных системах единиц
Максвелла уравнения - ур-ния, к-рым подчиняется (в пределах применимости классической ыакроскопич. электродинамики, см. Электродинамика классическая), электромагнитное поле в вакууме и сплошных средах.
1. Краткая история
Установлению M. у. предшествовал ряд открытий законов взаимодействий заряженных, намагниченных и токонесущих тел (в частности, законов Кулона, Био - Савара, Ампера). В 1831 M. Фарадей (M. Faraday) открыл закон эл.-магн. индукции и примерно в то же время ввёл понятие электрич. и магн. полей как самостоят, физ. субстанций. Опираясь на фарадеевское представление о поле и введя ток смещения, равнозначный по своему магн. действию обычному электрич. току, Дж. К. Максвелл (J. С. Maxwell, 1864) сформулировал систему ур-ний, названную впоследствии ур-ниями Максвелла. M. у. функционально связывают электрич. и магн. поля с зарядами и токами и охватывают собой все известные закономерности макроэлектромагнетизма. Впервые о M. у. было доложено на заседании Лондонского Королевского общества 27 окт. 18(34. Первоначально Максвелл прибегал к вспомогат. механич. моделям "эфира", но уже в "Трактате об электричестве и магнетизме" (1873) эл.-магн. поле рассматривалось как самостоят, физ. объект. Физ. основа M. у.- принцип близкодействия, утверждающий, что передача эл.-магн. возмущений от точки к точке происходит с конечной скоростью (в вакууме со скоростью света с). Он противопоставлялся ньютоновскому принципу дальнодействия, сводящемуся к мгновенной передаче воздействий на любое расстояние
 Матем. аппаратом теории Максвелла послужил векторный анализ, представленный в инвариантной форме через кватернионы Гамильтона. Сам Максвелл считал, что его заслуга состоит лишь в матем. оформлении идей Фарадея.
Матем. аппаратом теории Максвелла послужил векторный анализ, представленный в инвариантной форме через кватернионы Гамильтона. Сам Максвелл считал, что его заслуга состоит лишь в матем. оформлении идей Фарадея.2. Каноническая форма
Канонич. форма записи, принятая ныне, принадлежит Г. Герцу (H. Hertz) и О. Хевисайду (О. Heaviside) и основана на использовании не кватернионных, а векторных полей: напряжённости электрического поля E, напряжённости магнитного поля H, векторов электрической индукции D и магнитной индукции В.M. у. связывают их между собой, с плотностью электрического заряда
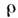 и плотностью электрического тока J, к-рые рассматриваются как источники:
и плотностью электрического тока J, к-рые рассматриваются как источники: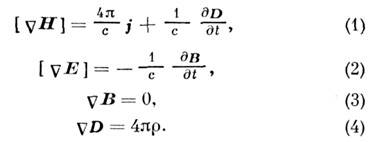
Здесь использована Гаусса система единиц (о записи M. у. в др. системах см. в разделе 15). Входящие в (1) - (4) величины E, D, j являются истинными, или полярными, векторами (а величина r - истинным скаляром), поля H к В- псевдовекторами, или аксиальными векторами. Все эти величины предполагаются непрерывными (вместе со всеми производными) ф-циями времени t и координат
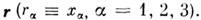 Следовательно, в ур-ниях (1) - (4) не учитывается ни дискретная структура электрич. зарядов и токов, ни квантовый характер самих полей. Учёт дискретности истинных источников может быть произведён даже в доквантовом (классич.) приближении с помощью Лоренца- Максвелла уравнений.
Следовательно, в ур-ниях (1) - (4) не учитывается ни дискретная структура электрич. зарядов и токов, ни квантовый характер самих полей. Учёт дискретности истинных источников может быть произведён даже в доквантовом (классич.) приближении с помощью Лоренца- Максвелла уравнений.3. Максвелла уравнения в интегральной форме
Используя Гаусса- Остроградского формулу и С такса формулу, ур-ниям (1) - (4) можно придать форму интегральных:
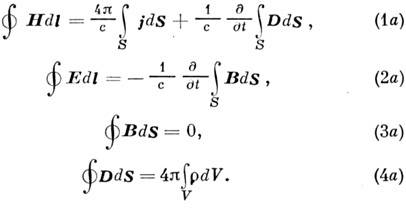
Криволинейные интегралы в (1a),(2a) берутся по произвольному замкнутому контуру (их наз. циркуляция-ми векторных полей), а стоящие в правых частях поверхностные интегралы - по поверхностям, ограниченным этими контурами (опирающимся на них), причём направление циркуляции (направление элемента контура
 ) связано с направлением нормали к S (вектор
) связано с направлением нормали к S (вектор 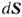 ) правовинтовым соотношением (если в качестве исходного выбрано пространство с правыми системами координат). В интегралах по замкнутым поверхностям (S). в (3а), (4а) направление вектора элемента площади
) правовинтовым соотношением (если в качестве исходного выбрано пространство с правыми системами координат). В интегралах по замкнутым поверхностям (S). в (3а), (4а) направление вектора элемента площади 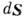 совпадает с наружной нормалью к поверхности; V- объём, ограниченный замкнутой поверхностью S.
совпадает с наружной нормалью к поверхности; V- объём, ограниченный замкнутой поверхностью S.M. у. в форме (1a) - (4a) предназначаются не только для изучения топологич. свойств эл.-магн. полей, но и являются удобным аппаратом решения конкретных задач электродинамики в системах с достаточно высокой симметрией или с априорно известными распределениями полей. Кроме того, в матем. отношении эта система ур-ний содержательнее системы (1) - (4), поскольку пригодна для описания разрывных, нодиффе-ренцируемых распределений полей. Но в отношении физ. пределов применимости обе системы ур-ний равнозначны, т. к. любые скачки полей в макроэлектродинамике должны рассматриваться как пределы микромасштабно плавных переходов, с тем чтобы внутри них сохранялась возможность усреднения ур-ний Лоренца - Максвелла. С этими оговорками резкие скачки можно описывать и в рамках M. у. (1) - (4), прибегая к аппарату обобщённых функций.
Наконец, M. у. в интегральной форме облегчают физ. интерпретацию MH. эл.-магн. явлений и поэтому нагляднее сопоставляются с теми экспериментально установленными законами, к-рым они обязаны своим происхождением. Так, ур-ние (1a) есть обобщение Био - Савара закона (с добавлением к току
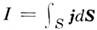 максвелловского смещения тока).
максвелловского смещения тока).Ур-ние (2a) выражает закон индукции Фарадея; иногда его правую часть переобозначают через "магн. ток смещения"
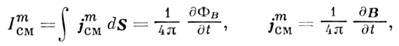
где
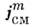 - плотность "магн. тока смещения", Ф В - магн. поток. Ур-ние (За) связывают с именем Гаусса
- плотность "магн. тока смещения", Ф В - магн. поток. Ур-ние (За) связывают с именем Гаусса  , установившим соленоидальность поля В, обусловленную отсутствием истинных магн. зарядов. Впрочем вопрос о существовании магнитных монополей пока остаётся открытым. Но соответствующее обобщение M. у. произведено (Хевисайд, 1885) на основе принципа двойственной симметрии M. у. (см. в разделе 9), для чего в (2) и (2a) наряду с магн. током смещения вводится ещё и "истинный" магн. ток (процедура, обратная проделанной когда-то Максвеллом с электрич. током в первом ур-нии), а в ур-ние Гаусса (3), (За) - магн. заряд
, установившим соленоидальность поля В, обусловленную отсутствием истинных магн. зарядов. Впрочем вопрос о существовании магнитных монополей пока остаётся открытым. Но соответствующее обобщение M. у. произведено (Хевисайд, 1885) на основе принципа двойственной симметрии M. у. (см. в разделе 9), для чего в (2) и (2a) наряду с магн. током смещения вводится ещё и "истинный" магн. ток (процедура, обратная проделанной когда-то Максвеллом с электрич. током в первом ур-нии), а в ур-ние Гаусса (3), (За) - магн. заряд 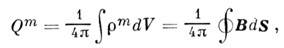
где
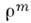 - плотность магн. заряда. Фактически все экспериментальные установки для регистрации ожидаемых магнитных монополей основаны на этом предположении. Наконец, ур-ние (4a) определяет поле свободного электрич. заряда; его иногда называют законом Кулона (Ch. A. Coulomb), хотя, строго говоря, оно не содержит утверждения о силе взаимодействия между зарядами, да и к тому же справедливо не только в электростатике, но и для систем с произвольным изменением поля во времени. На тех же основаниях иногда и ур-нпе (Ia) связывают с именем Ампера (A. Ampere).
- плотность магн. заряда. Фактически все экспериментальные установки для регистрации ожидаемых магнитных монополей основаны на этом предположении. Наконец, ур-ние (4a) определяет поле свободного электрич. заряда; его иногда называют законом Кулона (Ch. A. Coulomb), хотя, строго говоря, оно не содержит утверждения о силе взаимодействия между зарядами, да и к тому же справедливо не только в электростатике, но и для систем с произвольным изменением поля во времени. На тех же основаниях иногда и ур-нпе (Ia) связывают с именем Ампера (A. Ampere).4. Общая характеристика Максвелла уравнений
Совокупность M. у. (1) - (4) составляет систему из восьми (двух векторных и двух скалярных) линейных дифференц. ур-ний 1-го порядка для четырёх векторов
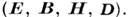 Источники (скаляр
Источники (скаляр 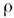 и вектор
и вектор 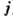 ) не могут быть заданы произвольно; применяя операцию
) не могут быть заданы произвольно; применяя операцию 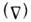 к ур-нию (1) и подставляя результат в (4), получаем:
к ур-нию (1) и подставляя результат в (4), получаем:
или в интегральной форме:
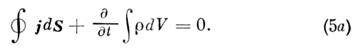
Это ур-ние непрерывности для тока, содержащее в себе закон сохранения заряда для замкнутых изолнров. областей
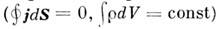 ,- один из фундам. физ. принципов, подтверждаемых в любых экспериментах.
,- один из фундам. физ. принципов, подтверждаемых в любых экспериментах.Ур-ния (1) - (4) распадаются на два самостоят, "блока": ур-ния (1) и (4), содержащие векторы
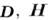 и источники
и источники 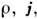 и ур-ния (2) и (3) - однородные ур-ния для
и ур-ния (2) и (3) - однородные ур-ния для 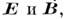 не содержащие источников. Ур-ння (2) и (3) допускают получение общего решения, в к-ром
не содержащие источников. Ур-ння (2) и (3) допускают получение общего решения, в к-ром 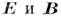 выражаются через т. H. потенциалы электромагнитного поля
выражаются через т. H. потенциалы электромагнитного поля 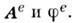 При этом ур-ние (3) "почти следует" из (2), т. к. операция (у), применённая к (2), даёт
При этом ур-ние (3) "почти следует" из (2), т. к. операция (у), применённая к (2), даёт 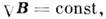 что отличается от (3) только константой, определяемой нач. условиями. Аналогично ур-ние (4) "почти следует" из (1) и ур-ния непрерывности (5).
что отличается от (3) только константой, определяемой нач. условиями. Аналогично ур-ние (4) "почти следует" из (1) и ур-ния непрерывности (5).Система M. у. (1) - (4) не является полной: по существу, она связывает 4 векторные величины двумя векторными ур-ниями. Её замыкание осуществляется путём добавления соотношений, связывающих векторы 1-го "блока"
 с векторами 2-го "блока"
с векторами 2-го "блока"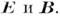 Эти соотношения зависят от свойств сред (материальных сред), в к-рых происходят эл.-магн. процессы, и наз. материальными ур-ниями (см. раздел 7).
Эти соотношения зависят от свойств сред (материальных сред), в к-рых происходят эл.-магн. процессы, и наз. материальными ур-ниями (см. раздел 7).5. Максвелла уравнения для комплексных амплитуд
В силу линейности системы (1) - (4) для её решений справедлив суперпозиции принцип. Часто оказывается удобным фурье-представление общего решения (1) - (4) как ф-ции времени (см. Фурье преобразование). Записывая временной фактор в виде
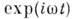 , для комплексных фурье-амплитуд
, для комплексных фурье-амплитуд 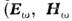 и т. д.) получаем систему ур-ний
и т. д.) получаем систему ур-ний 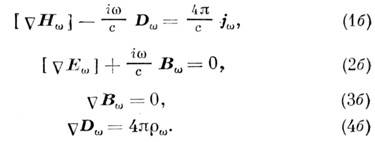
Система (1б) - (4б) в нек-ром смысле удобнее (1) - (4), ибо упрощает применение к эл.-динамич. системам, обладающим временной дисперсией (см. раздел 7), т. е. зависимостью параметров от частоты
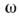
6. Алгебраические Максвелла уравнения
Если распространить (в силу линейности M. у.) фурье-разложение и на зависимость полей от пространственных координат, т. е. представить общее решение ур-ний (1) - (4) в виде суперпозиции плоских волн типа
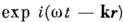 (k - волновой вектор), то для фурье-компонентов нолей
(k - волновой вектор), то для фурье-компонентов нолей  k и т. д.) получим систему алгебраич. ур-ний:
k и т. д.) получим систему алгебраич. ур-ний: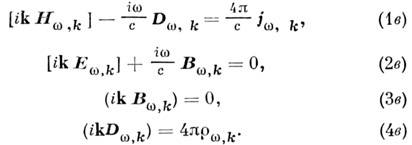
Такое сведение M. у. к набору ур-ний для осцилляторов (осцилляторов поля) составляет важный этап перехода к квантовой электродинамике, где эл.-магн. поле рассматривается как совокупность фотонов, характеризуемых энергиями
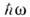 и импульсами
и импульсами 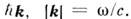 Однако и в макроэлектродинамике представления (1 в) - (4 в) оказываются иногда вполне адекватными физ. сущности процессов: напр., при выделении откликов высокодобротных систем (см. Объёмный резонатор) или при изучении "механизма формирования" мод со сложной пространственной структурой из набора плоских волн и т. п. Наконец, M. у. в форме (1 в) - (4 в) удобны для описания свойств эл.-динамич. систем, обладающих не только временной, но и пространственной дисперсией, если последняя задаётся в виде зависимости параметров от волнового вектора k.
Однако и в макроэлектродинамике представления (1 в) - (4 в) оказываются иногда вполне адекватными физ. сущности процессов: напр., при выделении откликов высокодобротных систем (см. Объёмный резонатор) или при изучении "механизма формирования" мод со сложной пространственной структурой из набора плоских волн и т. п. Наконец, M. у. в форме (1 в) - (4 в) удобны для описания свойств эл.-динамич. систем, обладающих не только временной, но и пространственной дисперсией, если последняя задаётся в виде зависимости параметров от волнового вектора k.7. Материальные уравнения
В макроэлектродинамике материальные связи, характеризующие эл.-магн. свойства сред, вводятся феноменологически; они находятся либо непосредственно из эксперимента, либо на основании модельных представлений. Существуют два способа описания: в одном векторы E и H считаются исходными и материальные ур-ния задаются в виде D = D(E , H )и В= В( Е, <Н), в другом - за исходные берутся векторы 2-го "блока" E и В, и соответствующие материальные связи представляются иначе: D = D(E,В), H= H(E, В). Оба описания совпадают для вакуума, где материальные уравнения вырождаются в равенства D = E и B = H.
Рассмотрим простейшую модель среды, характеризуемую мгновенным, локальным поляризац. откликом на появляющиеся в ней поля E и H. Под действием поля E в такой среде возникает электрич. поляризация
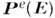 (см. Поляризации вектор), а под действием поля H- магн. поляризация
(см. Поляризации вектор), а под действием поля H- магн. поляризация 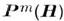 . Чаще её наз. намагниченностью и обозначают М.
. Чаще её наз. намагниченностью и обозначают М.Материальные ур-ния для таких сред имеют вид
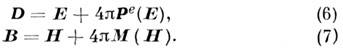
При этом индуцированные в среде электрич. заряды наз. связанными или поляризац. зарядами с плотностью
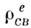 , а токи, обусловленные их изменениями,- поляризац. токами с плотностью
, а токи, обусловленные их изменениями,- поляризац. токами с плотностью 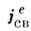 :
: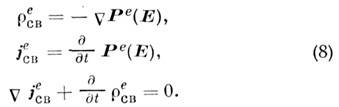
Эти понятия были перенесены и на магн. поля, что можно выразить в виде системы ур-ний, аналогичной
(8):
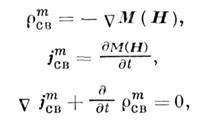
и только потом выяснилось, что истинными источниками намагничивания среды оказались электрич. токи
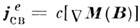 , а не магн. заряды. Поэтому терминология сложилась на основе физически некорректной системы
, а не магн. заряды. Поэтому терминология сложилась на основе физически некорректной системы 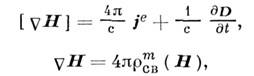
тогда как следовало бы принять беззарядовые ур-ния
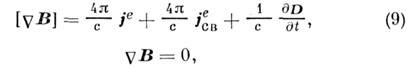
что равносильно замыканию исходных M. у. (1) - (4) с помощью материальных связей
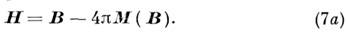
Из (6) и (7a) следует, что 2-й вариант представления материальных соотношений, в к-ром постулируются в качестве исходных векторы E и B, физически предпочтительнее.
В модели Лоренца - Максвелла усреднение микрополя Н микро, произведённое с учётом вклада со стороны индуциров. полей, приводит к ур-ниям (9) и соответственно < Н микро>= В. Однако обычно параметры сред вводятся с помощью ур-ний (7), что облегчает двойственную симметризацию ф-л (подробнее см. в разделе 9). Напр., скалярные восприимчивости сред (ce, cm) определяются соотношениями
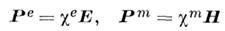
и позволяют ввести диэлектрическую проницаемостьe и магнитную проницаемость m:
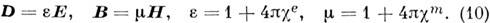
Простейшие модели сред характеризуются пост, значениями
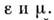 В случае вакуума
В случае вакуума 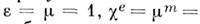 0.
0.Классификация разл. сред ооычно основывается на материальных ур-ниях типа (10) и их обобщениях. Если проницаемости e и m не зависят от полей, то M. у. (1) - (4) вместе с материальными ур-ниями (10) остаются линейными, поэтому о таких средах говорят как о линейных средах. При наличии зависимостей
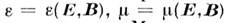 среды наз. нелинейными: решения M. у. в нелинейных средах не удовлетворяют принципу суперпозиции. Если проницаемости зависят от координат
среды наз. нелинейными: решения M. у. в нелинейных средах не удовлетворяют принципу суперпозиции. Если проницаемости зависят от координат 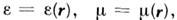 то говорят о неоднородных средах, при зависимости от времени
то говорят о неоднородных средах, при зависимости от времени 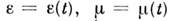 - о нестац попарных средах (иногда такие эл.-динамич. системы наз. параметрическими). Для анизотропных сред скаляры e, m в (10) заменяются на тензоры:
- о нестац попарных средах (иногда такие эл.-динамич. системы наз. параметрическими). Для анизотропных сред скаляры e, m в (10) заменяются на тензоры: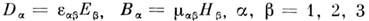 (по дважды встречающимся индексам производится суммирование). Важное значение имеют также эффекты запаздывания и нелокальности отклика среды на внеш. поля.
(по дважды встречающимся индексам производится суммирование). Важное значение имеют также эффекты запаздывания и нелокальности отклика среды на внеш. поля. Значение индуциров. поляризации Р е, напр, в момент г, может определяться, вообще говоря, значениями полей во все предыдущие моменты времени, т. е.
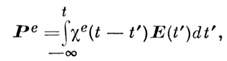
что при преобразовании Фурье по времени приводит к зависимости
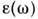 [соответственно
[соответственно  i]. Такие среды наз. средами с временной (частотной) дисперсией или просто диспергирующими средами. Аналогичная связь устанавливается и для нелокальных взаимодействий, когда отклик в точке г зависит от значения полей, строго говоря, во всех окружающих точках
i]. Такие среды наз. средами с временной (частотной) дисперсией или просто диспергирующими средами. Аналогичная связь устанавливается и для нелокальных взаимодействий, когда отклик в точке г зависит от значения полей, строго говоря, во всех окружающих точках 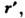 но обычно всё-таки в пределах нек-рой конечной её окрестности:
но обычно всё-таки в пределах нек-рой конечной её окрестности:  При преобразовании Фурье по г это приводит к появлению зависимостей
При преобразовании Фурье по г это приводит к появлению зависимостей 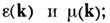 такие среды наз. средами с пространственной дисперсией (см. Дисперсия пространственная).
такие среды наз. средами с пространственной дисперсией (см. Дисперсия пространственная).В проводящих средах входящая в M. у. (1) - (5) плотность тока
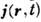 состоит из двух слагаемых: одно по-прежнему является сторонним током
состоит из двух слагаемых: одно по-прежнему является сторонним током 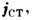 обусловленным заданным перемещением электрич. зарядов под действием сторонних сил (обычно неэлектрич. происхождения), а другое - током проводимости
обусловленным заданным перемещением электрич. зарядов под действием сторонних сил (обычно неэлектрич. происхождения), а другое - током проводимости  зависящим от полей, определяемых системой M. у., и связанным с ними материальными ур-ниями вида
зависящим от полей, определяемых системой M. у., и связанным с ними материальными ур-ниями вида 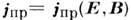 В простейшем случае эта зависимость сводится к локальному Ома закону,
В простейшем случае эта зависимость сводится к локальному Ома закону,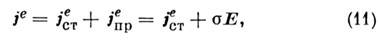
где
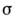 - электропроводность (проводимость) среды. Иногда в (11) вводят обозначение
- электропроводность (проводимость) среды. Иногда в (11) вводят обозначение  , благодаря к-рому различают системы с заданными токами и системы с заданными полями (напряжениями). Для синусоидальных во времени полей, подчинённых ур-ниям (1б) - (4б) и материальным связям (10) и (11), вводится комплексная диэлектрич. проницаемость, объединяющая (10) и (11),
, благодаря к-рому различают системы с заданными токами и системы с заданными полями (напряжениями). Для синусоидальных во времени полей, подчинённых ур-ниям (1б) - (4б) и материальным связям (10) и (11), вводится комплексная диэлектрич. проницаемость, объединяющая (10) и (11),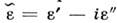 , мнимая часть к-рой обусловлена проводимостью и определяет диссипацию энергии эл.-магн. поля в среде. По аналогии вводится комплексная магн. проницаемость
, мнимая часть к-рой обусловлена проводимостью и определяет диссипацию энергии эл.-магн. поля в среде. По аналогии вводится комплексная магн. проницаемость 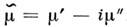 , мнимая часть к-рой обусловливает потери, связанные с перемагничиванием среды. Комплексные проницаемости в общем случае зависят от частоты w и волнового вектора
, мнимая часть к-рой обусловливает потери, связанные с перемагничиванием среды. Комплексные проницаемости в общем случае зависят от частоты w и волнового вектора 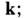 эти зависимости не могут быть произвольными: причинности принцип связывает их действительные и мнимые части Крамерса- Кронига соотношениями.
эти зависимости не могут быть произвольными: причинности принцип связывает их действительные и мнимые части Крамерса- Кронига соотношениями.В общем случае вид материальных ур-ний зависит также и от системы отсчёта, в к-рой эти ур-ния рассматривают. Так, если в неподвижной системе К среда характеризуется простейшими ур-ниями (10), то в инер-циальной системе К' , движущейся относительно К с пост, скоростью и, появляется анизотропия:
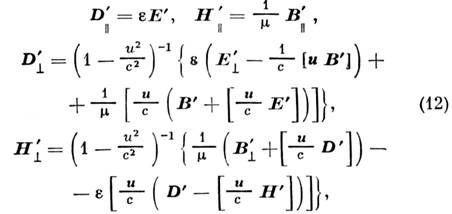
где индексы
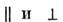 обозначают продольные и поперечные к
обозначают продольные и поперечные к 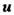 составляющие векторов. В рамках алгебраич. M. у. (1в) - (4в) материальные ур-ния (12) могут быть переписаны в виде
составляющие векторов. В рамках алгебраич. M. у. (1в) - (4в) материальные ур-ния (12) могут быть переписаны в виде 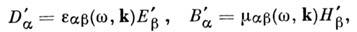
что можно трактовать как наличие временной и пространственной дисперсии. Исследование процессов с материальными связями типа (12) составляет предмет электродинамики движущихся сред. Заметим, что хотя характеристики е и m удобно симметризуют материальные ур-ния, их введение не является непременным условием замыкания M. у. Соответствующей перенормировкой допустимо свести описание магн. поля к одно-векторному, т. е. сделать
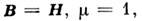 но при этом даже для изотропной среды диэлектрич. проницаемость становится тензором, она различна для вихревых и потенциальных полей. Физически это связано с неоднозначностью модельного представления диполь-ных моментов, во всяком случае при
но при этом даже для изотропной среды диэлектрич. проницаемость становится тензором, она различна для вихревых и потенциальных полей. Физически это связано с неоднозначностью модельного представления диполь-ных моментов, во всяком случае при 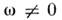 они могут равноправно интерпретироваться и как зарядовые, и как токовые.
они могут равноправно интерпретироваться и как зарядовые, и как токовые.8. Граничные условия
Поскольку M. у. справедливы для любых (в рамках применимости макроэлектродинамики) неоднородных сред, то в областях резкого изменения их параметров иногда можно игнорировать тонкую структуру распределения полей в переходном слое и ограничиться "сшиванием" полей по разные стороны от него, заменяя тем самым переходный слой матем. поверхностью - границей, лишённой толщины. Если внутри переходной области имелись заряды с объёмной плотностью
 или токи с объёмной плотностью
или токи с объёмной плотностью 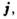 то при сжатии слоя в поверхность сохраняются их интегральные значения ·- вводятся поверхностные заряды r пов и поверхностные токи
то при сжатии слоя в поверхность сохраняются их интегральные значения ·- вводятся поверхностные заряды r пов и поверхностные токи 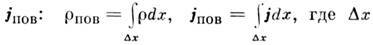 - толщина переходного слоя.
- толщина переходного слоя.Применение M. у. и ур-ния непрерывности приводит к следующим граничным условиям:
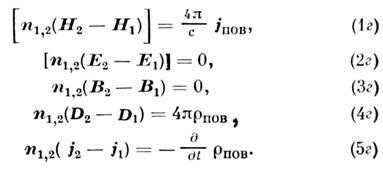
Здесь индексы 1 и 2 характеризуют поля по разные стороны от границы, а
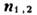 - единичный вектор нормали к поверхности, направленный из среды 1 в среду 2. Правила (1 г) - (5 г) пригодны для перехода через любые поверхности, независимо от того, совпадают ли они с границами раздела сред или проходят по однородным областям, поэтому их иногда наз. поверхностными M. у.
- единичный вектор нормали к поверхности, направленный из среды 1 в среду 2. Правила (1 г) - (5 г) пригодны для перехода через любые поверхности, независимо от того, совпадают ли они с границами раздела сред или проходят по однородным областям, поэтому их иногда наз. поверхностными M. у.Иногда граничные условия (1 г) - (5 г) порождают краевые условия, т. е. задают не правила перехода через границу, а сами поля на ней. Напр., внутри идеального проводника
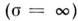 в силу (11)
в силу (11) 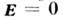 (иначе возник бы ток неограниченной плотности), поэтому на границе раздела диэлектрик - идеальный проводник в согласии с (2 г)
(иначе возник бы ток неограниченной плотности), поэтому на границе раздела диэлектрик - идеальный проводник в согласии с (2 г)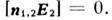 Такие границы наз. идеальными электрич. стенками. Аналогично вводится понятие идеальной магн. стенки, на к-рой
Такие границы наз. идеальными электрич. стенками. Аналогично вводится понятие идеальной магн. стенки, на к-рой 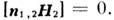 Если структура полей по одну сторону от границы универсальна, т. е. не зависит от распределения полей по др. сторону, то краевые условия могут состоять в задании не самих полей, а лишь связей между ними, напр.
Если структура полей по одну сторону от границы универсальна, т. е. не зависит от распределения полей по др. сторону, то краевые условия могут состоять в задании не самих полей, а лишь связей между ними, напр. 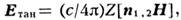 где Z- нек-рая скалярная или тензорная ф-ция координат границы (
где Z- нек-рая скалярная или тензорная ф-ция координат границы ( - тангенциальный компонент
- тангенциальный компонент 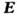 ). К условиям такого рода относится, в частности, Леонтовича граничное условие для синусоидально меняющихся во времени полей на поверхности хороших проводников.
). К условиям такого рода относится, в частности, Леонтовича граничное условие для синусоидально меняющихся во времени полей на поверхности хороших проводников.9. Двойственная симметрия Максвелла уравнений
Двойственная симметрия M. у. имеет место для любой формы их записи. Она состоит в инвариантности M. у. относительно линейных преобразований нолей, производимых по след, правилам:
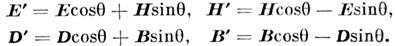
Здесь
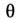 - произвольный угл. параметр; в частности, при
- произвольный угл. параметр; в частности, при 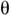 = О получаются тождественные преобразования, а при
= О получаются тождественные преобразования, а при  - стандартные преобразования перестановочной двойственности (операция
- стандартные преобразования перестановочной двойственности (операция 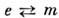 ): замена
): замена  даёт в областях, свободных от источников, новое решение M. у. При этом, однако, оно меняет местами ур-ния
даёт в областях, свободных от источников, новое решение M. у. При этом, однако, оно меняет местами ур-ния 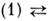
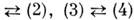 и, следовательно, там, где раньше были распределены электрич. источники, возникают источники магнитные
и, следовательно, там, где раньше были распределены электрич. источники, возникают источники магнитные 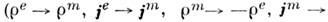
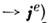 . Поэтому с точки зрения двойственной симметрии M. у. задание материальных связей в виде
. Поэтому с точки зрения двойственной симметрии M. у. задание материальных связей в виде 
 представляется вполне удобным. Дуально-симметричные M. у. обладают рядом достоинств, по крайней мере в чисто методич. плане. Так, напр., они симметризуют скачки тангенциальных компонентов магн. и электрич. полей и, если задание ffTall на поверхности идеальной электрич. стенки эквивалентно заданию поверхностного электрич. тока, то задание Я 1а„ на идеальной магн. стенке сводится к заданию магн. поверхностного тока:
представляется вполне удобным. Дуально-симметричные M. у. обладают рядом достоинств, по крайней мере в чисто методич. плане. Так, напр., они симметризуют скачки тангенциальных компонентов магн. и электрич. полей и, если задание ffTall на поверхности идеальной электрич. стенки эквивалентно заданию поверхностного электрич. тока, то задание Я 1а„ на идеальной магн. стенке сводится к заданию магн. поверхностного тока:Таким сведением задач с заданными
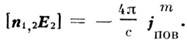 полями к задачам с заданными токами широко пользуются в теории дифракции волн, в частности в дифракции радиоволн.
полями к задачам с заданными токами широко пользуются в теории дифракции волн, в частности в дифракции радиоволн.Принцип перестановочной двойственности является представителем класса дискретных преобразований (см. Симметрия), оставляющих инвариантными M. у. Такого же сорта преобразованиями являются, в частности, операция обращения времени
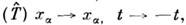
любые
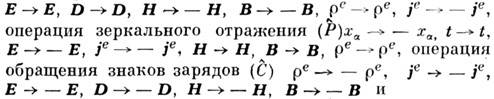
последовательно осуществляемые комбинации операций

10. Максвелла уравнения в четырёхмерном представлении
Придавая времени t смысл четвёртой координаты и представляя её чисто мнимой величиной
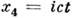 (см. Минковского пространство-время), можно заключить описание электромагнетизма в компактную форму. Эл.-магн. поле в 4-описании может быть задано двумя антисимметричными тензорами
(см. Минковского пространство-время), можно заключить описание электромагнетизма в компактную форму. Эл.-магн. поле в 4-описании может быть задано двумя антисимметричными тензорами 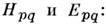

где
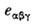 - Леви-Чивиты символ, лат. индексы пробегают значения 1, 2, 3, 4, а греческие - 1, 2, 3. В 4-век-торе тока объединены обычная плотность тока je и плотность электрич. заряда
- Леви-Чивиты символ, лат. индексы пробегают значения 1, 2, 3, 4, а греческие - 1, 2, 3. В 4-век-торе тока объединены обычная плотность тока je и плотность электрич. заряда 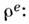
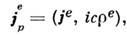
аналогично вводят 4-вектор магн. тока.
В этих обозначениях M. у. допускают компактное 4-мерное представление:
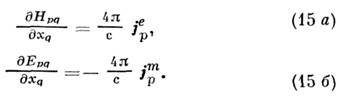
Взаимной заменой векторов поля и индукции в ф-лах (13),
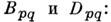 (14) вводятся тензоры индукции эл.-магн. поля
(14) вводятся тензоры индукции эл.-магн. поля 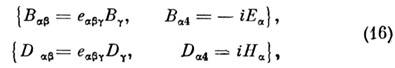
через к-рые также могут быть записаны M. у.:
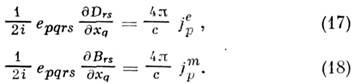
Любая пара тензорных ур-ний, содержащая в правых частях оба 4-тока (электрич. и мат.), тождественна системе M. у. Чаще используют пару ур-ний (15 а), (18), при этом материальные ур-ния сводятся к функциональной связи между тензорами
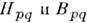 (последний чаще обозначают через
(последний чаще обозначают через 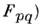 .
.Из антисимметрии тензоров поля, индукции и M. у. в форме (17) - (18) следует равенство нулю 4-дивергенций 4-токов:
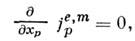
к-рое представляет собой 4-мерную запись ур-ний непрерывности для электрич. (магн.) зарядов. T. о., 4-векторы токов являются чисто вихревыми, и соотношения (17), (18) можно рассматривать как их представление в виде 4-роторов соответствующих тензоров. Наряду с представленным здесь вариантом часто используется также 4-мерное описание, в к-ром временная координата (обычно с индексом О) берётся действительной, но 4-мерному пространству приписывается гипербодич. сигнатура
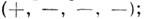 в таком пространстве приходится различать ко- и контравариантные компоненты векторов и тензоров (см. Ковариантность и контравариантность).
в таком пространстве приходится различать ко- и контравариантные компоненты векторов и тензоров (см. Ковариантность и контравариантность).11. Лоренц-инвариантность Максвелла уравнений
Все экспериментально регистрируемые эл.-динамич. явления удовлетворяют относительности принципу. Вид M. у. сохраняется при линейных преобразованиях, оставляющих неизменным интервал

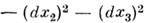 и составляющих 10-мерную Пуанкаре группу:4 трансляции
и составляющих 10-мерную Пуанкаре группу:4 трансляции 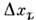 , 3 пространственных (орто-) поворота
, 3 пространственных (орто-) поворота  и 3 пространственно-временных (орто-хроно-) поворота, иногда называемых ло-ренцевыми вращениями. Последние соответствуют перемещениям системы отсчёта вдоль осей xa с пост, скоростями
и 3 пространственно-временных (орто-хроно-) поворота, иногда называемых ло-ренцевыми вращениями. Последние соответствуют перемещениям системы отсчёта вдоль осей xa с пост, скоростями 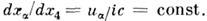 В частности, для
В частности, для 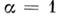 получается простейшая разновидность Лоренца преобразований:
получается простейшая разновидность Лоренца преобразований: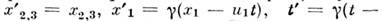
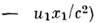 , где
, где 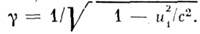 Соответственно поля преобразуются по правилам:
Соответственно поля преобразуются по правилам: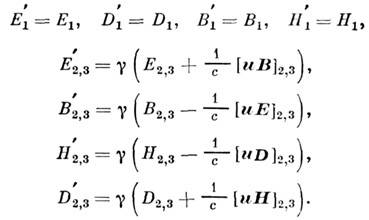
Релятивистски-ковариантная запись M. у. позволяет легко находить инвариантные комбинации полей, токов и потенциалов (4-скаляров или инвариантов Лоренца группы), сохраняющихся, в частности, при переходе от одной инерциальной системы отсчёта к другой. Во-первых, это чисто полевые инварианты (см. Инварианты электромагнитного поля). Во-вторых, это токовые (источниковые) инварианты:
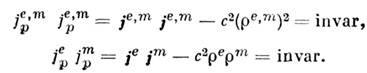
В-третьих, это потенциальные инварианты:
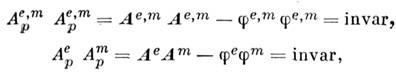
где
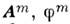 - магн. потенциалы (получающиеся из А е и
- магн. потенциалы (получающиеся из А е и 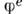 преобразованием перестановочной двойственности), источниками к-рых являются магн. токи jm и заряды
преобразованием перестановочной двойственности), источниками к-рых являются магн. токи jm и заряды 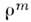 . И, наконец, многочисл. коыбиниров. инварианты типа
. И, наконец, многочисл. коыбиниров. инварианты типа  и им подобные. Число таких комбиниров. инвариантов (квадратичных, кубичных и т. д.) по полям н источникам неограниченно.
и им подобные. Число таких комбиниров. инвариантов (квадратичных, кубичных и т. д.) по полям н источникам неограниченно.12. Лагранжиан для электромагнитного поля
M. у. могут быть получены из наименьшего действия принципа, т. е. их можно совместить с Эйлера- Лаг-ранжа уравнениями, обеспечивающими вариационную акстремальность ф-ции действия:

здесь
 - лагранжиан, являющийся релятивистски-инвариантной величиной; интегрирование ведётся по 4-мерному объёму V, (t2 - t1) с фиксиров. границами. В качестве обобщённых координат принято обычно использовать потенциалы Аa. и f. Поскольку лагран-жев формализм должен давать полное (замкнутое) динамич. описание системы, то при его построении нужно принимать во внимание материальные ур-ния. Они фигурируют как зависимости связанных зарядов и токов от полей В и Е·
- лагранжиан, являющийся релятивистски-инвариантной величиной; интегрирование ведётся по 4-мерному объёму V, (t2 - t1) с фиксиров. границами. В качестве обобщённых координат принято обычно использовать потенциалы Аa. и f. Поскольку лагран-жев формализм должен давать полное (замкнутое) динамич. описание системы, то при его построении нужно принимать во внимание материальные ур-ния. Они фигурируют как зависимости связанных зарядов и токов от полей В и Е·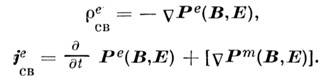
В результате лагранжиан принимает вид инвариантной комбинации полей, потенциалов и источников:
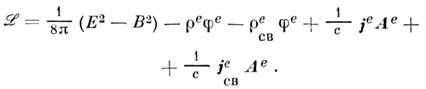
А ур-ния Эйлера - Лагранжа для нек-рой обобщённой координаты
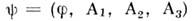 получают приравниванием нулю соответствующих вариационных производных:
получают приравниванием нулю соответствующих вариационных производных: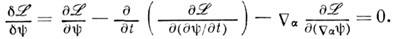
Для
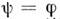 приходим к (4), для-
приходим к (4), для- 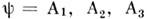 к ур-нию (1) в соответствующих обозначениях. Вариационный подход позволяет придать теории универсальную форму описания, распространяемую и на описания динамики любых взаимодействий, даёт возможность получать ур-ния для комбиниров. динамич. систем, напр, электромеханических. В частности, для систем с сосредоточенными параметрами, характеризуемых конечным числом степеней свободы, соответствующие ур-ния наз. ур-ниями Лагранжа - Максвелла.
к ур-нию (1) в соответствующих обозначениях. Вариационный подход позволяет придать теории универсальную форму описания, распространяемую и на описания динамики любых взаимодействий, даёт возможность получать ур-ния для комбиниров. динамич. систем, напр, электромеханических. В частности, для систем с сосредоточенными параметрами, характеризуемых конечным числом степеней свободы, соответствующие ур-ния наз. ур-ниями Лагранжа - Максвелла.13. Единственность решений Максвелла уравнений
Различают теоремы единственности для стационарных и нестационарных процессов. Условия единственности нестационарных решений извлекаются из Пойн-тинга теоремы, где источники считаются заданными ф-циями координат и времени. Если бы они порождали два разл. поля, то разность этих полей в вакууме (или в любой линейной материальной среде) вследствие принципа суперпозиции была бы решением однородных M. у. Для обращения этой разности в нуль и, следовательно, получения единств, решения достаточно удовлетворить след, трём условиям. 1) На поверхности S, окружающей область V, где ищется поле, должны быть заданы тангенциальные составляющие поля Е тан или поля Н тан либо соотношения между ними импедансного типа:
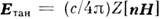 ( п - нормаль к S) со значениями Z, исключающими приток энергии извне. К таковым относятся, в частности, условия излучения (см. Зоммерфельда условия излучения), к-рым удовлетворяют волны в однородной среде на больших расстояниях от источников. Во всех случаях поток энергии для разностного поля вообще исчезает или направлен наружу (из объёма). 2) В нач. момент времени должны быть заданы все поля всюду внутри V.3) Плотность энергии электромагнитного поля
( п - нормаль к S) со значениями Z, исключающими приток энергии извне. К таковым относятся, в частности, условия излучения (см. Зоммерфельда условия излучения), к-рым удовлетворяют волны в однородной среде на больших расстояниях от источников. Во всех случаях поток энергии для разностного поля вообще исчезает или направлен наружу (из объёма). 2) В нач. момент времени должны быть заданы все поля всюду внутри V.3) Плотность энергии электромагнитного поля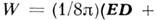 HB )должна быть положительна (вакуум, среды с
HB )должна быть положительна (вакуум, среды с 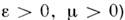 . Эта частная теорема единственности обобщается на среды с нелокальными связями, а также на нек-рые виды параметрич. сред. Однако в нелинейных средах, где принцип суперпозиции не работает, никаких общих утверждений о единственности не существует.
. Эта частная теорема единственности обобщается на среды с нелокальными связями, а также на нек-рые виды параметрич. сред. Однако в нелинейных средах, где принцип суперпозиции не работает, никаких общих утверждений о единственности не существует.В стационарных режимах нач. условия выпадают, и теоремы единственности формулируются непосредственно для установившихся решений. Так, в электростатике достаточно задать все источники re ст, все полные заряды на изолиров. проводниках или их потенциалы, чтобы при соответствующих условиях на бесконечности (нужное спадание поля) решение было бы единственным. Аналогичные теоремы устанавливаются для магнитостатики и электродинамики пост, токов в проводящих средах.
Особо выделяется случай синусоидальных во времени процессов, для к-рых формулируют след, признаки, достаточные для получения единств, решения: 1) задание источников
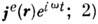 задание E тан или Н тан на ограничивающей объём V поверхности S или соответствующих импедансных условий, обеспечивающих отсутствие потока вектора Пойнтинга внутрь V;3) наличие малого поглощения внутри V или малой утечки энергии через S для исключения существования собств. колебаний на частоте
задание E тан или Н тан на ограничивающей объём V поверхности S или соответствующих импедансных условий, обеспечивающих отсутствие потока вектора Пойнтинга внутрь V;3) наличие малого поглощения внутри V или малой утечки энергии через S для исключения существования собств. колебаний на частоте 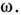
14. Классификация приближений Максвелла уравнений
Классификация приближений M. у. обычно основывается на безразмерных параметрах, определяющих и критерии подобия для эл.-магн. полей. В вакууме таким параметром является отношение
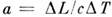 , где
, где 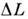 - характерный масштаб изменения полей (либо размер области, в к-рой ищется решение),
- характерный масштаб изменения полей (либо размер области, в к-рой ищется решение),  - характерный временной масштаб изменения полей.
- характерный временной масштаб изменения полей.а) а =0 - статич. приближение, статика.
Система M. у. распадается на три.
I.
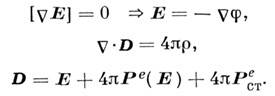
Материальная связь в простейшем случае имеет вид
 . Это система M. у. для электростатики, в к-рой источниками служат заданные распределения плотности электрич. заряда
. Это система M. у. для электростатики, в к-рой источниками служат заданные распределения плотности электрич. заряда 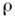 и сторонней поляризации
и сторонней поляризации 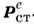 . В однородной среде
. В однородной среде 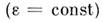 эл.-статич. потенциал f определяется Пуассона уравнением
эл.-статич. потенциал f определяется Пуассона уравнением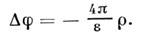
Для более сложных материальных <ур-ний различают электростатику анизотропных сред
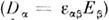 , нелинейную электростатику
, нелинейную электростатику 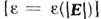 , электростатику сред с пространственной дисперсией
, электростатику сред с пространственной дисперсией 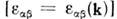 , важным частным случаем к-рых являются движущиеся среды с временной дисперсией (здесь может даже меняться тип ур-ния для потенциала с эллиптического на параболический) и т. п.
, важным частным случаем к-рых являются движущиеся среды с временной дисперсией (здесь может даже меняться тип ур-ния для потенциала с эллиптического на параболический) и т. п.II. Поля в магнитостатике описываются ур-ниями
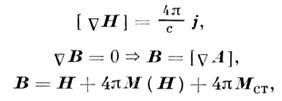
где в случае простейшей материальной связи индуци-ров. намагниченность определяется соотношением
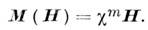
Источниками в ур-ниях магнитостатики являются заданные распределения плотности электрич. тока
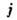 и сторонней намагниченности
и сторонней намагниченности 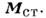 В однородной среде
В однородной среде  векторный потенциал магн. поля
векторный потенциал магн. поля 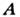 (калибровка кулоновская) определяется векторным ур-нием Пуассона
(калибровка кулоновская) определяется векторным ур-нием Пуассона 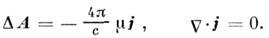
В общем случае возможны такие же разновидности сред, что и в электростатике.
III. K статич. электродинамике относят и процессы протекания пост, токов в распределённых проводящих средах. Токовая статика охватывается ур-ниями
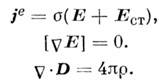
Источниками являются силы неэлектрич. происхождения, действующие на заряды, характеризующиеся напряжённостью
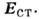 Электрич. заряды присутствуют лишь в местах неоднородности среды, напр, на границах проводящих сред. Распределение токов в проводящих средах сопоставимо с распределением электрич. и магн. полей в электростатике и магнитостатике. Часто благодаря этой аналогии говорят, напр., о магн. цепях, по к-рым "текут" магн. потоки
Электрич. заряды присутствуют лишь в местах неоднородности среды, напр, на границах проводящих сред. Распределение токов в проводящих средах сопоставимо с распределением электрич. и магн. полей в электростатике и магнитостатике. Часто благодаря этой аналогии говорят, напр., о магн. цепях, по к-рым "текут" магн. потоки 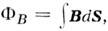 аналогичные электрич. токам
аналогичные электрич. токам 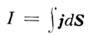 в электрич. цепях.
в электрич. цепях. б)
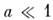 - квазистатика, обобщающая соответствующие статич. приближения.
- квазистатика, обобщающая соответствующие статич. приближения.В квазиэлектростатике вакуумные электрич. поля описываются ур-ниями статики (I.), а в ур-ниях для магн. поля в качество заданного источника фигурирует и ток смещения. Квазимагнитостатика описывается статич. ур-ниями для магн. полей с учётом закона индукции (2) для электрич. поля. Поскольку вихревое электрич. поле меняет электрич. токи в проводниках, являющиеся источниками магн. поля, то этот раздел квазистатики более богат, чем предыдущий; он описывает широкий круг явлений, происходящих в цепях перем, тока с сосредоточенными параметрами: ёмкостями, индуктивностями и сопротивлениями.
Квазистатика в распределённых проводящих средах описывается ур-ниями квазистационарного (квазистатического) приближения, в к-рых током смещения пренебрегают по сравнению с токами проводимости. В этом приближении распределения электрич. токов, электрич. и магн. полей описываются одинаковыми ур-ниями диффузионного типа:
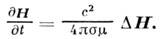
Эти ур-ния определяют, напр., распределение токов Фуко, проникновение перем. эл.-магп. поля в проводник (скин-эффект )и т. п.
в)
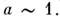 Резонансные волновые поля описываются точной системой M. у., однако их иногда выделяют из общего класса полей, особенно в тех случаях, когда их структура (пространственное распределение) фиксируется границами области, внутри к-рой эти поля могут быть возбуждены (напр., внутри полых резонаторов с металлическими стенками или в поперечном сечении волноводов либо в окрестности тонкой проволочной или щелевой антенны). При этом обычно обращаются к фурье-преобразованию M. у. и представлению поля в виде набора дискретных или квазидискретных мод.
Резонансные волновые поля описываются точной системой M. у., однако их иногда выделяют из общего класса полей, особенно в тех случаях, когда их структура (пространственное распределение) фиксируется границами области, внутри к-рой эти поля могут быть возбуждены (напр., внутри полых резонаторов с металлическими стенками или в поперечном сечении волноводов либо в окрестности тонкой проволочной или щелевой антенны). При этом обычно обращаются к фурье-преобразованию M. у. и представлению поля в виде набора дискретных или квазидискретных мод.г)
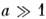 . В рамках этого неравенства существуют ква-зиоптич. и оптич. приближения (см. Квазиоптика, Геометрической оптики метод), относящиеся к протяжённым в масштабе длины волны распространениям полей (волновым пучкам, многомодовым конфигурациям и т. п.). Под характерным масштабом, входящим в параметр а, здесь подразумевается масштаб изменения амплитуды поля.
. В рамках этого неравенства существуют ква-зиоптич. и оптич. приближения (см. Квазиоптика, Геометрической оптики метод), относящиеся к протяжённым в масштабе длины волны распространениям полей (волновым пучкам, многомодовым конфигурациям и т. п.). Под характерным масштабом, входящим в параметр а, здесь подразумевается масштаб изменения амплитуды поля.15. Максвелла уравнения в различных системах единиц
Выше использовалась симметричная гауссова абс. система единиц. Удобство гауссовой системы единиц состоит в том, то все 4 вектора поля
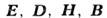 обладают в ней одинаковыми размерностями
обладают в ней одинаковыми размерностями 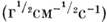 и потому в классическом "линейном" вакууме можно избежать введения ненужных констант: в силу
и потому в классическом "линейном" вакууме можно избежать введения ненужных констант: в силу 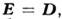
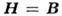 безразмерные проницаемости вакуума обращаются в единицы
безразмерные проницаемости вакуума обращаются в единицы  Др. достоинством одинаковой размерности эл.-магн. полей является их ес-теств. объединение в единые тензоры поля вида (13), (14) без внесения корректирующих множителей.
Др. достоинством одинаковой размерности эл.-магн. полей является их ес-теств. объединение в единые тензоры поля вида (13), (14) без внесения корректирующих множителей.Если принять запись ур-ния непрерывности в форме (5), а также соблюдение принципа дуальной симметрии, то M. у. можно придать вид
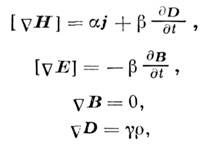
где константы
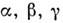 связаны соотношением
связаны соотношением 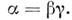
Для простейших материальных связей типа (10) можно ввести проницаемости вакуума
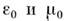 и относит, проницаемости среды
и относит, проницаемости среды 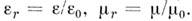 Тогда из волнового ур-ния в вакууме следует естеств. соотношение между константами
Тогда из волнового ур-ния в вакууме следует естеств. соотношение между константами 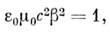
где с- скорость распространения любого эл.-магн. возмущения (в частности, света) в вакууме. В гауссовой системе
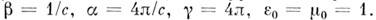
Существует операция рационализации, предложенная Хевисайдом и состоящая в устранении иррациональных числовых множителей из M. у. Простейший путь
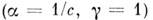 принят в рационализов. системе Xe-висайда - Лоренца.
принят в рационализов. системе Xe-висайда - Лоренца.В Международной системе единиц (СИ) возникает дополнительная размерная константа, наз. импедансом (или характеристическим сопротивлением) вакуума
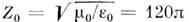 Ом. Это представляет известные удобства при сопоставлении процессов распространения плоских волн в свободном пространстве с волнами напряжения и тока в линиях передач, но приходится приписывать вакууму размерные значения проницаемостей:
Ом. Это представляет известные удобства при сопоставлении процессов распространения плоских волн в свободном пространстве с волнами напряжения и тока в линиях передач, но приходится приписывать вакууму размерные значения проницаемостей: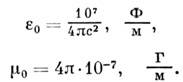
Значения коэф. в СИ:
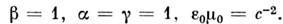
Лит.: Ландау Л. Д., Лифшиц E. M., Теория поля, 7 изд., M., 1988; их же, Электродинамика сплошных сред, 2 изд., M., 1982; Власов А. А., Макроскопическая электродинамика, M., 1955; Никольский В. В., Теория электромагнитного поля, 3изд., M., 1964; Джексон Д ж., Классическая электродинамика, пер. с англ., M., 1965; Каценеленбаум Б. 3., Высокочастотная электродинамика, M., 1966; Стражев В. И., Томильчик Л. M., Электродинамика с магнитным зарядом, Минск, 1975; Медведев Б. В., Начала теоретической физики, M., 1977; Новожилов Ю. В., Яппа Ю. А., Электродинамика, M., 1978; Туров E. А., Материальные уравнения электродинамики, M., 1983; Fущич В. И., Hикитин А. Г., Симметрия уравнений Максвелла, К., 1983; Бредов M. M., Румянцев В. В., Tоптыгин И. H., Классическая электродинамика, M., 1985.
M. А. Миллер, E, В. Суворов.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
