КОНДО ЭФФЕКТ

КОНДО ЭФФЕКТ

       

аномальная температурная зависимость уд. электрич. сопротивления нек-рых нормальных металлов (Au, Ag, Cu, Al, Zn и др.): при понижении темп-ры уд. сопротивление этих металлов r проходит через минимум при т. н. т е м п е р а т у р е К о н д о ТK, а затем возрастает, приближаясь к конечному пределу r0. К. э. обнаружен экспериментально в кон. 50-х гг., был объяснён япон. физиком Кондо в 1964. Причина К. э.— присутствие в металле примесных атомов Mn, Fe, Cr, Со и др. с незаполненными электронными оболочками, обладающими отличным от нуля магн. моментом (см. ПАРАМАГНЕТИК). ТK варьируется в широком интервале, напр. в случае Zn с примесью Mn: TK=1К, а в Аl с примесью Mn: ТK=500К.

Рассеяние эл-на проводимости на парамагн. атоме может сопровождаться переворотом спинов эл-на и примесного атома. Своеобразный хар-р зависимости такого рассеяния от энергии эл-на проводимости и приводит к К. э. Рост уд. сопротивления при понижении темп-ры ниже ТK; прекращается, когда начинается упорядочение ориентации спинов примесных атомов, т. е. возникает ферромагнетизм или антиферромагнетизм. При этом ориентация спинов примесных атомов фиксируется и исчезает возможность рассеяния с переворотом спина. Др. проявление К. э.— уменьшение сопротивления в магн. поле, связанное с фиксацией спинов примесных атомов внеш. магн. полем.

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

КОНДО ЭФФЕКТ

- аномальная температурная зависимость электросопротивления сплавов немагн. металлов (Си, Al, Ag, La, Lu и др.) с небольшим кол-вом магн. примесей - атомов переходных (Fe, Сг, Со, V) или редкоземельных (Се, Yb, Tm) элементов. Аномалия состоит в том, что при понижении темп-ры электросопротивление R таких сплавов сначала убывает по закону, типичному для немагн. металлов, а затем при нек-рой характерной темп-ре Т _K (т е м п - р а К о н-д о) проходит через минимум и далее остаётся конечным при 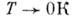(рис. 1). К. э. имеет квантовый характер и обусловлен антиферромагн. обменным взаимодействием электронов проводимости немагн. металла с магн. 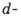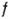примесями - атомами с незаполненными или -электронными оболочками, ионы к-рых в металле обладают магн. моментами.

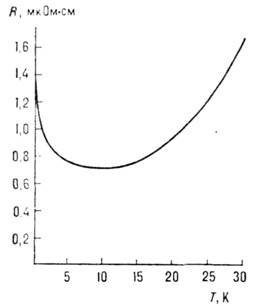
Рис. 1. Зависимость электросопротивления R сплава (LaCl)Al₂ (0,63 ат. % Сl) от температуры Т.

Необычные свойства рассеяния электронов проводимости на примесных атомах, вызванного этим взаимодействием (рассеяние электрона может сопровождаться переворотом спинов электрона и примесного атома), приводят к ярко выраженным аномалиям кинетич., термич. и магн. свойств таких сплавов. Наблюдаются отрицат. магнетосопротивление (рис. 2), гигантский пик в температурной зависимости термоэдс, максимум в температурной зависимости теплоёмкости и т. д. Магн. примеси понижают темп-ру сверхпроводящего перехода немагн. металла, а также при достаточной концентрации могут привести к явлению т. н. возвратной сверхпроводимости: при дальнейшем понижении темп-ры сплав из сверхпроводящей фазы переходит в нормальную, а затем при дальнейшем понижении темп-ры вновь становится сверхпроводником. Описанные аномальные явления, экспериментально обнаруженные в 30-х гг. 20 в., были систематически исследованы в 60-х гг. В результате этого экспериментально установлен универсальный характер поведения магн. примеси в немагн. металле с темп-рой Т _К, характерной для каждого сплава. Т _К изменяется в широком диапазоне: напр., от 1К (для LaCe) до 300К (для AuV). При этом эффекты пропорц. концентрации примеси (т. е. не зависят от межпримесных корреляций) вплоть до концентрации примеси от 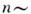10% для атомов переходных элементов до 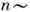1% для редкоземельных.

Аномальные явления объясняются тем, что амплитуда I обменного рассеяния (см. Амплитуда рассеяния )электронов проводимости на примеси, приводящего к изменению проекции магн. момента примеси на направление спина электронов, эффективно растёт с понижением темп-ры Т или магн. поля Я. В результате роста эфф. взаимодействия электроны проводимости создают повыш. спиновую плотность вокруг атома примеси и полностью компенсируют её магн. момент. Вследствие этого при понижении темп-ры атом примеси теряет магн. момент и примесный вклад в электросопротивление возрастает. Компенсация магн. момента проявляется в экспериментах, напр. при понижении темп-ры ниже T_K магн. восприимчивость перестаёт расти и остаётся конечной при Т. ОК.

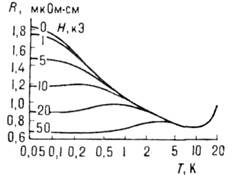
Рис. 2. Зависимость электросопротивления сплава (LaCl)Al₂ от температуры при различных величинах поля H (отрицательное магнитосопротивление).

Первый шаг к теоретич. описанию этого явления был сделан Дж. Кондо (J. Кондо, 1964), к-рый в рамках простейшей модели рассмотрел вклад обменного взаимодействия электронов проводимости с примесными атомами в первом неборновском приближении. Оказалось, что эфф. взаимодействие логарифмически растёт при понижении Т. В 1965 А. А. Абрикосов и Д. Сул (D. Sou-1е) для 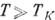установили соотношение [1, 2, 3]:

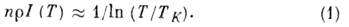
Здесь темп-pa Кондо 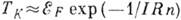, где 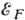- энергия Ферми, 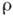- плотность состояний при 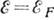, I - амплитуда обменного рассеяния зонного электрона на примесном атоме, R - электросопротивление, п- концентрация электронов. Тем самым были объяснены логарифмич. рост электросопротивления R сплавов при уменьшении Т:

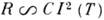
( С - концентрация примеси), и прекращение роста магн. восприимчивости 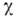вблизи Т _к:

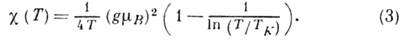
Здесь 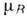- магнетон Бора, 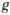- гиромагн. отношение для иона. Соотношения (1-3) справедливы при 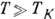, когда обменное взаимодействие невелико

В 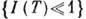области 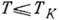обменное взаимодействие уже не мало и методы теории возмущения не позволяют описать поведение магн. примеси. Проблема теоретич. описания низкотемпературных свойств магн. примеси в немагн. металле получила назв. проблемы Кондо. В дальнейшем применение идей и методов ренормализационной группы[Ф. У. Андерсон (Ph. W. Anderson), К. Г. Уилсон (К. G. Wilson) и др.], а также феноменологич. теории ферми-жидкостей (П. Нозьер, P. J. Nozieres, 1974) позволило выяснить, что обнаруженный в рамках теории возмущения рост эфф. обменного взаимодействия при понижении темп-ры продолжается и при 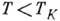и приводит к сильной связи примесного иона с электронами проводимости при Т=0 К [1]. Это означает полную компенсацию магн. момента примесного иона электронами проводимости и тем самым образование максимума плотности состояний р на поверхности Ферми. В результате этого осн. состояние атома примеси оказывается синглетным (её магн. момент при Т=0 К исчезает при 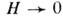, магн. восприимчивость 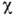остаётся конечной при Т=0 К, а все физ. величины при 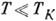становятся регулярными ф-циями T, H и др. с масштабом энергии 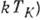. Напр., магн. восприимчивость

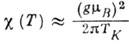(4)

Теплоёмкость

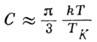(5)

Электросопротивление R определяется соотношением

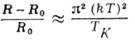(6)

Здесь 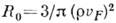, 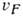- скорость электрона на поверхности Ферми. Подобное поведение известно в теории ферми-жидкости. Более того, между значениями 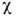и С при ТОК имеют место соотношения с коэф., характерными для теории ферми-жидкости.

Полное решение проблемы Кондо и др. моделей, описывающих динамику образования локализованного магн. момента в металле (учитывающих электронную структуру атома примеси, эффекты внутрикристалли-ческого поля и пр.), было получено в 1980 методами теории квантовых интегрируемых систем [4-5]. Мн. тра-диц. модели, описывающие электронные свойства сплавов немагн. металлов с магн. атомами, оказались "интегрируемыми" и были решены точно. В рамках этого решения были вычислены термодинамич. ф-ции сплавов при произвольных Т и Н и полностью описано образование максимума плотности состояний на поверхности Ферми. Тем самым удалось проследить за плавным переходом примеси из магн. состояния в немагнитное при понижении Т. Явление роста интенсивности взаимодействия при понижении энергии имеет место во многих важных проблемах физики конденсированных сред и физики частиц высоких энергий и является одной из важных проблем квантовой теории поля.

Лит.:1) Абрикосов А. А., Основы теории металлов, М., 1987; 2) S u h I H., Dispersion theory of the Kondo effect, "Phys. Rev. A", 1965, v. 138, p. 515; 3) Gruner G.,Z a-wadowski A., Magnetic impurities in non-magnetic metals, "Repts Progr. Phys.", 1974, v. 37, p. 1497; 4) Т s v e-1 i с k A. M., Wiegmann P. В., Exact results in the theory of magnetic alloys, "Adv. Phys.", 1983, v. 32, p. 453; 5) A n d-rei N., Furuya K., Lowenstein J. H., Solution of the Kondo problem, "Revs Mod. Phys.", 1983, v. 55, p. 331.

П. Б. Вигман.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.