- ЗЕЕБЕКА ЭФФЕКТ
- ЗЕЕБЕКА ЭФФЕКТ
-
возникновение электродвижущей силы в электрич. цепи, состоящей из последовательно соединённых разнородных проводников, контакты между к-рыми имеют разл. темп-ру. Открыт в 1821 нем. физиком Т. И. Зеебеком (Th. J. Seebeck). (см. ТЕРМОЭДС).
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- ЗЕЕБЕКА ЭФФЕКТ
-
- возникновение эдс (термоэдс) в электрич. контуре, состоящем из двух проводников А и В, контакты между к-рыми поддерживаются при разных темп-pax T1 и Т2. Открыт в 1821 Т. И. Зеебеком (Th. J. Seebeck). 3. э. используется для прямого преобразования тепловой энергии в электрическую (термоэлектрогенераторы) и в термометрии. Термоэдс контура определяется ф-лой:
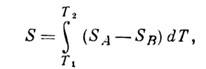
где SA п SB наз. абсолютными термоэдс (дифференц. термоэдс, коэф. термоэдс) проводников А и В, Абс. термоэдс - характеристика проводника, равная S=du/dT, где и - эдс, возникающая в проводнике при наличии в нём градиента темп-р. 3. э. связан с др. термоэлектрическими явлениями (Пельтье эффектом и Томсона эффектом )соотношениями Кельвина:
где r и П - коэф. Томсона и Пельтье. <Градиент темп-ры создаёт в проводнике градиент концентраций "холодных" и "горячих" носителей заряда. В результате этого возникают два диффузионных потока носителей - вдоль и против градиента темп-ры. Т. к. скорости диффузии и концентрации "горячих" и "холодных" носителей заряда различны, то на одном конце проводника создаётся избыточный положит. заряд, а на другом - отрицательный. Поле этих зарядов приводит к установлению стационарного состояния: число носителей, проходящих через поперечное сечение образца в обоих направлениях, одинаково. Возникающая диффузионная термоэдс определяется температурной зависимостью концентрации носителей заряда и их подвижностью m, обусловленной характером их взаимодействия с фононами, примесями и т. д. <В металлах электронный газ вырожден и термоэдс определяется только различием подвижностей "горячих" и "холодных" электронов. В полупроводниках термоэдс обусловлена зависимостью от Т как подвижности, так и концентрации электронов и дырок. Обычно вклад в термоэдс, связанный с температурной зависимостью концентрации носителей, превышает вклад, обусловленный различием в m(T), хотя последний в полупроводниках (вследствие Больцмана распределения носителей) на неск. порядков больше, чем в металлах. Именно поэтому термоэдс в полупроводниках значительно выше, чем в металлах. Теоретическое описание. Выражение для термоэдс может быть получено из кинетич. ур-ния Больцмана:
где величины К1 п К0 определяются ф-лой: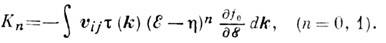
Здесь v - скорость носителей (i, j = x, у, z), t - время их релаксации, h - химический потенциал, f0 - ф-ция распределения Ферми, е - заряд носителей, E - их энергия, k - волновой вектор. <Для металлов выражение (3) принимает вид: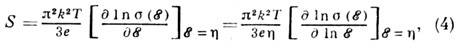
где s(E) - проводимость при T=К. Спомощью (4) может быть описана термоэдс кристаллич., аморфных и жидких металлов. Для металлов величина S порядка kT/h, т. к., с одной стороны, электронный газ вырожден и только малая часть электронов (порядка kT/h)участвует в диффузионном токе, с др. стороны, для большинства механизмов рассеяния зависимость проводимости от энергии слабая: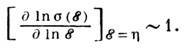
Однако существуют механизмы релаксации, для к-рых термоэдс в металлах порядка k/e. К ним относятся процессы асимметричного упругого и неупругого рассеяния электронов в ферромагнетиках с немагнитными примесями; процессы интерференции рассеяния, независящего от спинового взаимодействия электронов с примесью в кондо-решётках. В этих случаях [ дln s(E)/ дlnE]E=h~h/kТ. В приближении t=t0Er, где r - параметр, зависящий от природы процессов рассеяния, из (3) следует: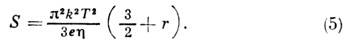
Для полупроводников в случае квадратичного изотропного дисперсии закона носителей из (3) следует: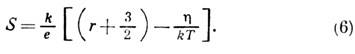
Знак термоэдс определяется знаком носителей заряда. Первый член суммы в (6) связан с изменением подвижности, а второй - с изменением концентрации носителей. Аналогичный вид имеет зависимость S(Т )для аморфных и стеклообразных полупроводников. Влияние "увлечения" электронов фононами и магнонами. Диффузионная термоэдс рассматривалась выше в предположении, что фононная система находится в равновесии. В действительности наличие градиента темп-ры вызывает отклонение фононной системы от равновесия - возникает поток фоноиов от "горячего" конца проводника к "холодному". Взаимодействуя с электронной системой, они передают им свой избыточный импульс, в результате чего возникает дополнит. т. н. термоэдс фононного увлечения S ф (см. Увлечение электронов фононами,[4]). Она определяется характеромэлектронно-фононного взаимодействия и зависит от др. механизмов рассеяния фононов. Если фононная система полностью релаксирует на электронах (эффект "насыщения"), то при T<<qD (qD- Дебая температура) S ф~T-1. S ф~T3 как для металлов, так и для полупроводников. Если же фононы взаимодействуют не только с электронами, но и друг с другом, зависимость S ф(T) иная. В металлах при T>>qD. В полупроводниках электроны взаимодействуют только с длинноволновыми фононами (см. Рассеяние носителей заряда в полупроводниках), а S ф определяется их взаимодействием с коротковолновыми фононами, к-рым длинноволновые фононы передают свой импульс: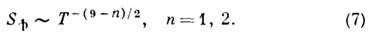
Два значения п соответствуют двум механизмам фонон-фононной релаксации, в к-рых либо учитывается (n=1), либо не учитывается ( п=2)затухание тепловых фононов. При низких темп-pax гл. роль играют процессы рассеяния на границах образца: S ф~DT3/2, где D - характерный размер образца. <В магнетиках существует эффект "увлечения" электронов магнонами, к-рый также вносит вклад в термоэдс (см. Спиновые волны). Для металлов с многолистной ферми-поверхностъю и полупроводников с многозонным характером проводимости выражения для диффузионной термоэдс и термоэдс увлечения обобщаются: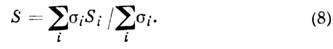
Здесь si и Si - парциальные вклады в проводимость и термоэдс i -го листа поверхности Ферми или i -й энергетич. зоны.3. э. в сверхпроводниках. Под действием градиента темп-ры в сверхпроводниках появляется объёмный ток нормальных возбуждений по природе такой же, как и в обычных проводниках. Этот ток обусловливает объёмный ток куперовских пар, к-рый компенсирует ток нормальных возбуждений. Т. к. полный объёмный ток равен 0, а электрич. поле в сверхпроводниках отсутствует, исследовать термоэдс, связанную с нормальными возбуждениями в сверхпроводниках, можно, измеряя сверхпроводящую компоненту тока. Лит.: Ландау Л. Д., Л и ф ш и ц Е. М., Электродинамика сплошных сред, 2 изд., М., 1982; Цидильковский И. М., Термомагнитные явления в полупроводниках, М., 1960; Зырянов П. С., К л и н г е р М. И., Квантовая теория явления электронного переноса в кристаллических полупроводниках, М., 1976; Термоэлектродвижущая сила металлов, пер. с англ., М., 1980; Абрикосов А. А., Основы теории металлов, М., 1987. И. М. Цидильковский, В. А. Матвеев.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
