РАССЕЯНИЕ НОСИТЕЛЕЙ ЗАРЯДА

РАССЕЯНИЕ НОСИТЕЛЕЙ ЗАРЯДА

в кристаллич. твёрдых телах - процесс взаимодействия электрона проводимости (дырки) с нарушениями идеальной периодичности кристалла, сопровождающийся переходом электрона из состояния с импульсом p в состояние с импульсом 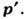Рассеяние наз. упругим, если энергии электрона в начальном и конечном состояниях равны, 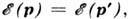или неупругим, если 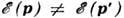. Источником упругого рассеяния являются статич. дефекты - примесные атомы, дислокации, границы кристаллич. зёрен и т. п. ( см. Дефекты в кристаллах). Осн. источником неупругого рассеяния являются колебания кристаллической решётки. Рассеяние электрона на колебаниях решётки описывается в терминах испускания и поглощения фононов движущимся электроном. В нек-рых случаях существенно неупругое рассеяние на др. квазичастицах- магнонах, плазмонах. Особое положение занимает Р. н. з. друг на друге (см. Межэлектронное рассеяние).

Р. н. з. является причиной того, что любое неравновесное по энергии или импульсу распределение электронов, созданное внеш. возмущением (электрич. поле, свет), с течением времени релаксирует к равновесному фермиевскому распределению 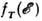, соответствующему темп-ре кристалла Т. В процессе релаксации упругое рассеяние "размешивает" распределение равномерно в пределах каждой изоэнергетич. поверхности 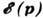= const, а неупругое - устанавливает равновесное распределение 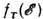между изоэнергетич. поверхностями с разными 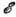. Время, необходимое для достижения равномерного распределения на изоэнергетич. поверхности, наз. временем релаксации импульса или транспортным временем релаксации. 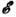Время, необходимое для установления равновесного распределения в области энергий порядка , наз. временем релаксации энергии . Если,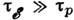 рассеяние наз. квазиупругим. В этом случае установление равновесия идёт в 2 этапа: сначала быстро (за время 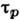) неравновесное распределение выравнивается на каждой изоэнергетич. поверхности и превращается в неравновесное распределение по энергиям, к-рое затем медленно (за время 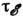) релаксирует к равновесному распределению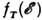

Возмущением, ответственным за Р. н. з., является разность между истинным потенциалом V(r, t), действующим на электрон в реальном кристалле, и периодич. потенциалом V₀(r, t), действующим в идеальном кристалле с неподвижными атомами (r- пространственная координата электрона). Возмущение dV = V- V₀ определяет вероятность рассеяния 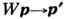. В вырожден ных полупроводниках и металлах следует учитывать принцип Паули, так что фактич. вероятность перехода равна 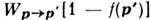. Кроме того, при большой плотности носителей рассеяние ослабляется экранированием возмущения из-за перераспределения носителей в пространстве.

Рассеяние на фононах. Вероятность рассеяния электрона при испускании или поглощении фонона о импульсом q. и энергией 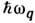(без учёта принципа Паули) определяется выражением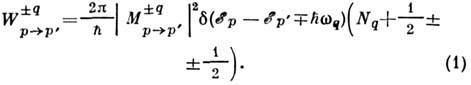

Здесь верх. и ниж. знаки соответствуют испусканию и поглощению фонона; числа фононов с импульсом q определяются распределением Планка (см. Планка закон излучения):

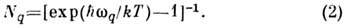
Матричный элемент М перехода p : p' содержит закон сохранения квазиимпульса: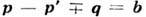(b- произвольный вектор обратной решётки). Переходы, для к-рых b = 0, наз. нормальными; если b.0, говорят о переходах с перебросом (см. Переброса процессы). Дельта-функция d отражает закон сохранения энергии. Вероятность рассеяния с испусканием фонона 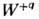пропорц. N_q+ 1. Два слагаемых, соответствующие N_q и 1, дают вероятности индуцированного и спонтанного рассеяний. Вероятность рассеяния с поглощением фонона 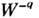пропорц. N_q, поэтому поглощение фонона всегда является индуцированным.

Рассеяние электрона на фононах в большой степени определяется законами сохранения энергии и импульса (кинематич. факторы), а также принципом Паули. Поэтому картина рассеяния различна для акустич. и оп-тич. фононов, имеющих разные законы дисперсии , и зависит от степени вырождения электронного газа. Кинематика позволяет установить, какие фононы дают осн. вклад в рассеяние, какова степень упругости рассеяния, а также является ли оно индуцированным или спонтанным.

Рассеяние на акустических фононах в полупроводниках. Т. к. скорость электрона v имеет порядок скорости звука s только при очень малой его энергии (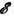! ms² ! 0,1 К), то в реальных условиях 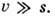Это означает, что возмущение, создаваемое акустич. фононом, почти статично, а рассеяние электронов всегда квазиупруго. Из кинематики следует, что осн. вклад в рассеяние вносят фононы с импульсом 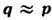; поэтому

направленный импульс электрона теряется всего за неск. столкновений. Энергия фонона с таким импульсом 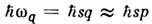!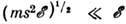, так что для релаксации энергии требуется много столкновений, т. е. действительно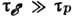

Является ли рассеяние индуцированным или спонтанным, зависит от соотношения между энергией фонона hsp и тепловой энергией Т. Эти величины сравниваются, когда энергия электрона равна Если 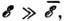то характерны N_q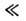1; доминирует спонтанное испускание фононов (динамич. трение), и "движение" электрона по оси энергии 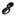есть систематич. дрейф вниз. При 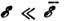доминируют индуциров. переходы, т. к. При этом испускание происходит не намного чаще, чем поглощение, и "движение" электрона по оси энергий превращается в диффузию.

Рассеяние на акустических фононах в металлах и вырожденных полупроводниках. Вследствие закона сохранения импульса наиб. вероятно взаимодействие с фононами, импульс к-рых 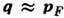, где 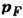- импульс Ферми (см. Ферми-поверхность). Но испусканию таких фононов (с энергией 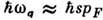) может препятствовать принцип Паули, если превышение энергии электрона 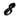над энергией Ферми 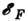много меньше , а поглощение может ослабляться из-за малого числа таких фононов, если 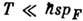. Поэтому характер рассеяния сильно зависит от Г и превышения энергии электрона над энергией Ферми. При 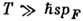почти для всех электронов 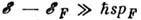(указанные ограничения несущественны) и рассеяние (с испусканием и поглощением) идёт на фононах с 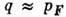и энергией 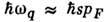. Для релаксации импульса требуется неск. столкновений, а для релаксации энергии - много (квазиупругое рассеяние). При 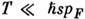поглощение фононов с энергией 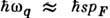маловероятно, но если 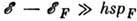, то принцип Паули не запрещает испускание таких фононов (в осн. спонтанное). Рассеяние, как и при высоких темп-pax, квазиупруго. Если же , то принцип Паули разрешает только испускание фононов с 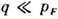. Такое рассеяние является малоугловым, и выравнивание распределения электронов на поверхности Ферми происходит диффузионно. Для полной релаксации импульса требуется много столкновений, релаксация же энергии происходит за неск. столкновений (неупругое рассеяние).

Рассеяние на оптических фононах. При рассеянии в металлах существенны оптич. фононы во всей зоне Бриллюэна, в осн. коротковолновые с 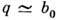, где b₀ - размер Бриллюэна зоны. В полупроводниках в рассеянии участвуют только оптич. ДВ-фононы с 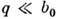. Частоту этих фононов w₀ можно считать не зависящей от q. Рассеяние на оптич. фононах квазиупруго только при 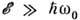! 400 К, т. е. только при очень высоких энергиях электронов (см. Горячие электроны). В области энергий 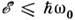проявляются неупругий и пороговый характеры рассеяния. Это существенно при низких темп-pax 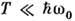, когда ниже порога () рассеяние слабое и возможно только за счёт маловероятного поглощения фонона, пропорционального 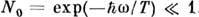, а выше порога (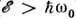) рассеяние сильное - оно происходит при спонтанном испускании фонона.

Деформационное и поляризационное рассеяния. В

выражение (1) входит матричный элемент М возмущения dV на блоховских ф-циях y (см. Блоховские электроны), обычно dV и y неизвестны, поэтому М можно найти только численными расчётами. Однако если рассеяние происходит на ДВ-фононах, эту трудность можно обойти. Для этого следует усреднить dV по объёму с размерами, большими постоянной решётки а₀ и меньшими длины волны фонона l = 2p/q. В результате усреднения появляется электрич. макрополе еf. Для dV, созданного акустич. фононом, f(r, t) (r - координата точки, в окрестности к-рой произведено усреднение) представляет собой электрич. поле, сопровождающее волну деформации (пьезополе). В случае оптич. фонона f(r, t) - поле, возникающее из-за относит. смещения разноимённо заряженных подрешё-ток (см. Динамика кристаллической решетки). Рассеяние, обусловленное электрич. макрополем, наз. поляризационным. Матричные элементы 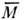для рассеяния, обусловленного макрополем, можно вычислять, представляя волновые ф-ции электрона в виде плоских волн.

Др. источником рассеяния является микрополе 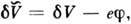выпавшее при усреднении. В области усреднения, где еf почти постоянно, dV - почти периодич. ф-ция r. В этой области электрон движется в периодич. поле V₀ +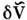и его закон дисперсии 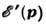отличается от закона дисперсии 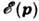в идеальной решётке. В др. области усреднения будут другие 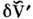и другие 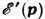. Т. к. частоты фононов меньше электронных, то закон дисперсии "следит" за колебаниями решётки, Т. о., в кристалле, в к-ром возбуждены ДВ-фононы, закон дисперсии медленно меняется в пространстве и времени; он описывается ф-цией 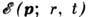, характерные масштабы изменения к-рой такие же, как у f(r, t). Двигаясь в среде с перем. законом дисперсии, электрон рассеивается (как свет в мутной среде), даже если макрополе отсутствует. Такое рассеяние наз. д е-формационным.

Матричные элементы 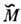деформац. рассеяния тоже можно вычислять, заменяя блоховские ф-ции на плоские волны, если в качестве возмущения брать не 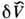, а т. н. деформац. потенциал w(r, t). В полупроводнике с невырожденной зоной w(r, t )имеет смысл сдвига дна или потолка зоны в точке r в момент t, т. е. w(r, t) =-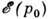, где р ₀ соответствует экстремуму зоны (или центру долины; в многодолинном полупроводнике деформац. потенциал различен для электронов разных долин). В металле w(r, t)- сдвиг поверхности Ферми, так что wзависит дополнительно от положения p на поверхности Ферми.

Матричные элементы в случае поляризационного 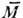и деформационного 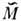рассеяний, вычисленные через еf и w, всегда сдвинуты по фазе на p/2. Это означает, что поляризац. и деформац. рассеяния, обусловленные одной и той же фононной модой, не интерферируют. Поэтому говорят о четырёх механизмах рассеяния: DA, DO, PA, PO, где первая буква указывает на характер рассеяния (деформационный или поляризационный), вторая - на ветвь фононов (акустическая или оптическая).

Для вычисления 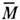и 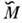необходимо выразить еср и wчерез смещения атомов решётки. Связь f со смещениями атомов находят из Пуассона уравнения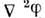= = 4pdivP, где P - дипольный момент единицы объёма, возникший при однородной статич. деформации решётки из-за смещений ядер и связанного с этим смещения электронов. Для деформации, созданной акустич. фононами 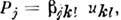" где u_kl- тензор деформации, а 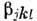выражаются через пьезомодули. При деформации, созданной оптич. фононами 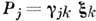, где | - вектор относит. смещения подрешёток, а g_jk выражаются через статич. и динамич. диэлектрич. проницаемости (см. ниже).

Число независимых констант b и g определяется симметрией кристалла. Так, в кубич. кристаллах с центром инверсии 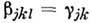= 0, так что поляризац. рассеяние невозможно. В кубич. кристалле с двумя атомами в элементарной ячейке (большинство полупроводников) возможно поляризац. рассеяние для акустич. и оптич. фононов.

Деформац. потенциал w(r, t )определяется смещениями атомов в точке r в момент t. Для акустич. фононов w.= 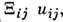для оптич. фононов - w = Здесь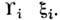

- т. н. константы деформац. потенциала. Их число, кроме симметрии кристалла, зависит ещё от положения р ₀ в полупроводниках или на поверхности Ферми в металлах. В кубич. полупроводнике с р₀ = 0 из симметрии следует, что и 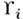= 0. Это значит, что w =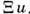, где и = и₁₁ + и₂₂ + и₃₃ - относит. изменение объёма при деформации. Т. к. для поперечных акустич. фононов и = 0, то DA -рассеяние разрешено только для продольных фононов, DО -рассеяние запрещено для обеих ветвей. Если р₀. лежит не в центре зоны Бриллюэна, то возможны DA- и DО -рассеяния на поперечных акустич. фононах.

Времена релаксациии 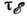можно найти, если вычислить, с какой скоростью электрон с импульсом p. теряет энергию и направленный импульс при рассеянии, переходя во все др. состояния с импульсами р' (скорость релаксации). В изотропном случае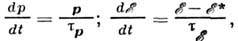

где величина 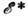имеет порядок тепловой энергии Т, если электронный газ невырожден, и равно ферми-энер-гии 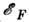, если газ сильно вырожден (здесь и ниже k =1). Для акустич. фононов в полупроводниках при ин-дуциров. рассеянии 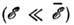скорость релаксации

импульса пропорц. Т:

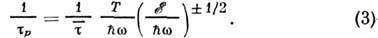
Здесь Т и 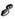выражены в долях энергии фонона; верх. знак относится к DA -рассеянию, нижний - к РА- рассеянию;. - характерное время, определяемое соотношениями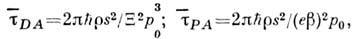

где r - плотность кристалла, р ₀ - импульс электрона с энергией 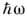. Типичные значения 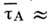1-10 пс. При 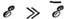(спонтанное рассеяние) скорость релаксации импульса, т. е.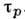, от Т не зависит:

Здесь 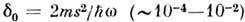- степень упругости рассеяния, m - эфф. масса электрона.

Время релаксацииэнергиине 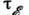зависит от соотношения между 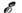и

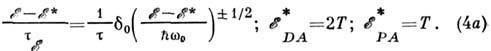
Для акустич. фононов в металлах и вырожденных полупроводниках при высоких темп-pax (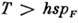) 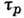определяется ф-лой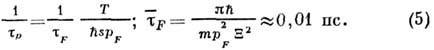

Скорость релаксации энергии

При низких темп-pax 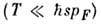и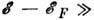

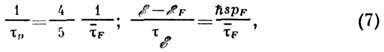
а для

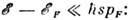
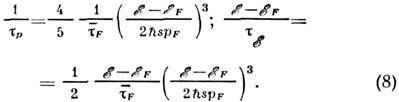
При рассеянии на оптич. фононах в полупроводниках в области квазиупругого рассеяния

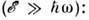
Здесь верх. знак относится к DО -рассеянию, нижний - к РО -рассеянию: =

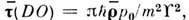
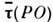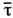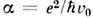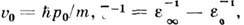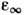= (¹/₂)aw (типичные значения =0,1-1 пс); здесь - плотность приведённой массы разноимённо заряженных подрешёток, - фрёлиховская константа связи,где и 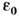- высокочастотная и статическая диэлектрические проницаемости решётки. Время релаксации энергии

Рассеяние на примесных атомах. При рассеянии на примесных атомах возмущение dV обусловлено элект-рич. полем (если примесь заряжена) и деформацией решётки в окрестности примеси. Иногда нужно учитывать обменные силы и магн. момент примеси. В случае заряж. примесей (примесных ионов) в полупроводниках вклад в dV от деформации решётки несуществен. Т. к. в полупроводнике p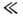b₀, то изменение импульса электрона при упругом рассеянии мало, а это значит, что рассеяние на больших расстояниях (r 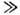а₀) определяется сглаженным потенциалом dV(r). Такой потенциал не зависит от микроструктуры примеси и имеет кулоновский вид:

где Ze- заряд иона. Поэтому время релаксации импульса 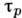можно вычислить, пользуясь Резерфорда формулой для сечения рассеяния заряж. частиц. Согласно этой ф-ле, дифференц. сечение рассеяния электрона под углом 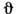в телесном угле dW: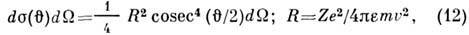

где u- скорость электрона. Для вычисления 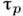необходимо усреднить s по всем . При интегрировании (12) по получают расходящийся интеграл, т. е. бесконечно большое сечение рассеяния. В действительности сечение рассеяния на примесном ноне конечно, т. к. кулоновский характер поля dV на больших расстояниях от примеси искажается полем др. примесных ионов и экранирующим полем электронов. Если учитывать первый фактор и "обрезать" кулоновский потенциал на ¹/₂ расстояния между примесными центрами, равного N^-1/3(N- концентрация примесей), то это приводит к ф-ле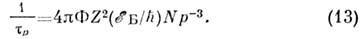

Здесь 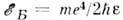- боровская энергия, F = In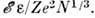

Ф-ла (13) носит назв. Конуэлл- Вайскопфа формулы.

Если учитывать также экранирование кулоновского поля примесного иона свободными носителями заряда, то обрезание потенциала осуществляется его умножением на ехр(-r/l), где l - длина экранирования. При этом в ф-ле (13) F = ln(1- х) - х ²/(1 + x²), где x= 2p/l ( Брукса- Херринга формула).

Рассеяние на нейтральных примесях в полупроводниках обусловлено кулоновскими и обменными силами, действующими между рассеивающимся электроном и атомом примеси. Используя аналогию с рассеянием на атоме водорода, обычно пользуются т. н. ф-лой Эр-гинсоя:

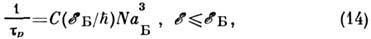
где 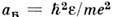- боровский радиус, С= 20.

В металлах возмущение dV сильно зависит от сочетания атомов примеси и матрицы, поэтому к.-л. общие ф-лы для 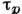получить не удаётся. Обычно сечение рассеяния 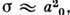однако оно сильно возрастает при резонансном рассеянии электронов на примесных атомах с незаполненными d- и f -оболочками, когда на примеси существуют виртуальные уровни энергии (см. Кондо эффект).

Экспериментальные методы. Сказанное выше относилось к рассеянию носителей внутри одной зоны (долины) с энергетич. спектром носителей, вырожденным только по ориентации спина. В более сложных ситуациях (вырожденные зоны, многодолинные полупроводники) трудно определить теоретически, какой механизм рассеяния доминирует в той пли иной области темп-р и энергий носителей. Поэтому осн. источником сведений о механизме Р. н. з. является эксперимент. Механизм рассеяния импульса обычно определяют по измерению подвижности носителей зарядаm = ( е/т) т _р и по ширине линии циклотронного резонанса Dw_c = 1/т _p. Входящее сюда т _r усреднено по энергии. Для невырожденного полупроводника усреднение сводится к замене 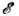на Т. Поэтому, изучая температурные зависимости m или Dw_c, можно отличить рассеяние на примесях, когда m 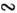T³/², от рассеяния на акустич. фононах, когда m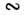T^-1/² для деформационного или m 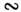T^1/2 для поляризационного рассеяний.

Механизм релаксации энергии раскрывается в экспериментах с горячими электронами по зависимости m или Dw_c от сильного электрич. поля или по спектрам горячей люминесценции.

Лит.: Конуэлл Э., Кинетические свойства полупроводников в сильных электрических полях, пер. с англ., М., 1970; Вир Г. Л., Пикус Р. Е., Симметрия и деформационные эффекты в полупроводниках, М., 1972; Wiley J. D., Mobility of holes in III-V Compounds, в кн.: Semiconductors and semimetals, v. 10, N. Y., 1975, p. 91; Гантмахер В. Ф., Лев и неон И. Б., Рассеяние носителей тока в металлах и полупроводниках, М., 1984. И. Б. Левинсон.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.