ВРАЩЕНИЯ ПОВЕРХНОСТЬ

- поверхность, описываемая вращением плоской кривой L вокруг оси, лежащей в ее плоскости. Если Lопределяется уравнениями то радиус-вектор В. п. есть

,

где и - параметр кривой 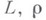- расстояние точки поверхности от оси вращения, - угол поворота. Линейный элемент В. п.:

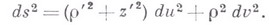
Гауссова кривизна 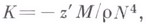средняя кривизна

где

Линии u=const наз. параллелями В. п. и представляют собой окружности, расположенные в плоскости, перпендикулярной оси вращения, с центрами на этой оси. Линии наз. меридианами; все они конгруэнтны вращаемой кривой и лежат в плоскостях, проходящих через ось вращения. Меридианы и параллели В. п. являются линиями кривизны и образуют изотермическую сеть.

В. п. допускает изгибание также в В. п., при к-ром сеть линий кривизны сохраняется и является потому главным основанием изгибания. Омбилические точки В. п. расположены на тех широтах, на к-рых центр кривизны меридиана лежит на оси вращения. Произведение радиуса параллели на косинус угла, под к-рым геодезии, линия В. п. пересекает параллель, постоянно вдоль геодезической (теорема Клеро).

Единственная минимальная В. п.- катеноид. Линейчатая В. п. есть однополостный гиперболоид или его вырождения: цилиндр, конус или плоскость. В. п., имеющая более одной оси вращения, есть сфера или плоскость. И.X. Сабитов.