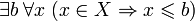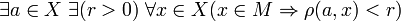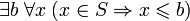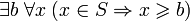Ограниченное числовое множество

Ограниченное числовое множество

В математическом анализе, и прилегающих разделах математики, ограниченное множество — множество, которое в определенном смысле имеет конечный размер. Базовым является понятие ограниченности числового множества, которое обобщается на случай произвольного метрического пространства, а также на случай произвольного частично упорядоченного множества.

Ограниченное числовое множество

Множество действительных чисел 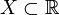$X \subset \mathbb{R}$ называется ограниченным сверху, если существует число b, такое что все элементы X не превосходят b:

$\exists b \; \forall x \; (x \in X \Rightarrow x \leqslant b)$

Множество действительных чисел 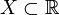$X \subset \mathbb{R}$ называется ограниченным снизу, если существует число b, такое что все элементы X не меньше :b: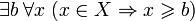 $\exists b \; \forall x \; (x\in X \Rightarrow x \geqslant b)$

Множество 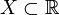$X \subset \mathbb{R}$, ограниченное сверху и снизу, называется ограниченным.

Множество 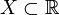$X \subset \mathbb{R}$, не являющееся ограниченным, называется неограниченным. Как следует из определения, множество не ограничено тогда и только тогда, когда оно не ограничено сверху или не ограничено снизу.

Примером ограниченного множества является отрезок $[a, b] = \{ a \leqslant x \leqslant b\}$,

неограниченного — множество всех целых чисел $\mathbb{Z} = \{ \ldots, -2, -1, 0, 1, 2, \ldots\}$,

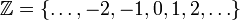ограниченного сверху, но неограниченного снизу — луч x < 0,

ограниченного снизу, но неограниченного сверху — луч x > 0.

Вариации и обобщения

Ограниченное множество в метрическом пространстве

Пусть (X,ρ) — метрическое пространство. Множество 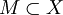$M \subset X$ называется ограниченным, если оно содержится в некотором шаре B_r(a):

$\exists a \in X \; \exists (r > 0) \; \forall x \in X (x \in M \Rightarrow \rho(a, x) < r)$

Множество, не являющееся ограниченным, называется неограниченным.

В отличие от числовой прямой, в произвольном метрическом пространстве нельзя ввести понятия ограниченного сверху и ограниченного снизу множеств.

Помимо понятия ограниченного множества для произвольного метрического пространства существует более специальное понятие вполне ограниченного множества. В случае числовых множеств это понятие совпадает с понятием ограниченного множества.

Ограниченность в частично упорядоченном множестве

Понятия ограниченного сверху, ограниченного снизу и просто ограниченного множества можно ввести в произвольном частично упорядоченном множестве. Эти определения буквально повторяют соответствующие определения для числовых множеств.

Пусть 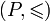$(P, \leqslant)$ — частично упорядоченное множество, 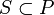$S \subset P$. Множество S называется ограниченным сверху, если

$\exists b \; \forall x \; (x \in S \Rightarrow x \leqslant b)$

ограниченным снизу, если

$\exists b \; \forall x \; (x \in S \Rightarrow x \geqslant b)$

Множество, ограниченное и сверху и снизу, называется ограниченным.

См. также

• Точная верхняя и нижняя грани