- ВИНЕРА ИНТЕГРАЛ
- абстрактный интеграл лебе-говского типа по множествам бесконечномерного функционального пространства от функционалов, определенных на этих множествах. В. и. введен Н. Винером (N. Wiener) в 20-х гг. 20 в. в связи с вопросами броуновского движения (см. [1], [2]).
Пусть
- векторное пространство непрерывных функций 
, определенных на [0, 1] и таких, что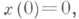 
с нормой 
Квазиинтервалом этого пространства наз. множество
}
(
и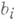 
могут равняться, соответственно, 
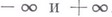, но тогда знак 
заменяется на 
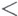). Примером квазиинтервала может служить все пространство
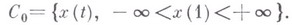
Мерой Винера квазиинтервала Qназ. число
и
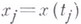. Эта мера распространяется до 
-аддитивной меры, определенной на борелевском теле множеств, порожденном квазиинтервалами (по-прежнему наз. мерой Винера). Пространство 
измеримо в смысле меры Винера и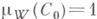 
Пусть
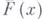-функционал, определенный на 
и измеримый относительно меры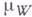 
. Интеграл
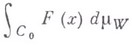
лебеговского типа наз. интегралом Винера, или интегралом по мере Винера от функционала
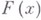. Если 
измеримо, то
где
- характеристич. функция множества Е. В. и. обладает рядом свойств обычного интеграла Лебега. В частности, ограниченный и измеримый на множестве Ефункционал интегрируем по мере Винера на этом множестве и если, кроме того, функционал F(х).непрерывен и неотрицателен, то
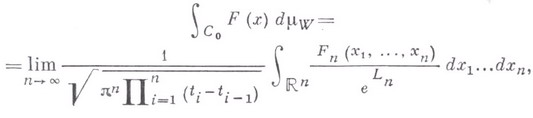
где
- значение функционала Fна ломаной с вершинами в 
.
Вычисление В. и. даже для сравнительно простых функционалов представляет значительную трудность. Иногда эту задачу удается свести к нахождению решения некоторого дифференциального уравнения (см. [1]).
Существует метод приближенного вычисления В. и. путем аппроксимации его конечномерными Стилтьеса интегралами высокой кратности.
Лит.:[1] Ковальчик И. М., "Успехи матем. наук", 1963, т. 18, в. 1, с. 97-134; [2] Шилов Г. Е., там же, в. 2, с. 99-120. В. И. Соболев.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
