ЦЕНТР

- тип расположения траекторий автономной системы обыкновенных дифференциальных уравнений 2-го порядка

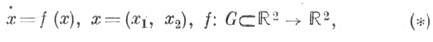
G- область единственности, в окрестности особой точки x₀. Этот тип характеризуется следующим образом. Существует окрестность . точки x₀ такая, что все траектории системы, начинающиеся в являются замкнутыми кривыми, окружающими х ₀. Ц. наз. при этом и сама точка x₀. На рис. точка О- центр. Движение по траекториям с возрастанием tможет происходить по часовой стрелке или против нее (как указано на рис. стрелками). Ц. устойчив по Ляпунову (не асимптотически). Его индекс Пуанкаре равен 1.
Точка х ₀ является для системы (*) Ц., напр., когда f(x)=-A( х-х₀), где А - постоянная матрица с чисто мнимыми собственными значениями. В отличие от простых точек покоя других типов, встречающихся для линейных систем 2-го порядка ( седло, узел, фокус), точка х ₀ типа Ц. при возмущении линейной системы добавками к правой части, вообще говоря, не остается Ц., как бы ни были высоки порядок малости возмущений относительно и порядок их гладкости. Она может перейти при этом в фокус (устойчивый или неустойчивый) или в центрофокус (см. Центра, и фокуса проблема). Для нелинейной системы (*) класса точка покоя x₀ может быть Ц. и в том случае, когда матрица А =f' (х ₀ )имеет два нулевых собственных значения.

Лит.:[1] Амелькин В. В., Лукашевич Н. А., Садовский А. П., Нелинейные колебания в системах второго порядка, Минск, 1982. См. также лит. при статье Особая точка дифференциального уравнения.
А. Ф. Андреев.