- ХОЛЛОВА ПОДГРУППА
- подгруппа конечной группы, порядок к-poй взаимно прост с ее индексом. Название связано с именем Ф. Холла (Ph. Hall), к-рый в 20-х гг. 20 в. начал изучать такие подгруппы в конечных разрешимых группах.
В конечном
-отделимой группе существует холлова 
-подгруппа (X. п., порядок к-рой делится только на простые числа из 
а индекс взаимно прост с любым числом из 
и все холловы 
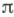-подгруппы сопряжены. Конечная разрешимая группа для любого множества 
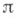простых чисел обладает холловой 
-подгруппой. Любая 
-подгруппа конечной разрешимой группы содержится в холловой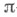 
-подгруппе и все холловы 
-подгруппы сопряжены. Любая холлова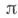 
-подгруппа является силовской 
-подгруппой. Для нормальной X. п. Нконечной группы G в Gвсегда существует дополнение, то есть такая подгруппа D, что 
и 
- единичная подгруппа; все дополнения для Н в G сопряжены. Если в группе есть нильпотентная холлова 
-подгруппа, то все холловы 
-подгруппы сопряжены и любая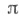 
-подгруппа содержится в нек-рой холловой 
-подгруппе. В общем случае X. п. не обладает такими свойствами. Напр., знакопеременная группа А 5 порядка 60 не имеет холловой {2, 5}-подгруппы. В А 5 есть холлова {2, 3}-подгруппа порядка 12, но подгруппа порядка 6 не лежит ни в какой холловой. Наконец, в простой группе порядка 168 холловы {2, 3}-подгруппы не сопряжены. Лит.:[1] Чунихин С. А., Подгруппы конечных групп, Минск, 1964; [2] Итоги науки и техники. Алгебра. 1964, М., 1966, с. 7-46; [3] Нuрреrt В., Endliche Gruppen, v. 1, В., 1979; [4] Reviews on finite groups, Providence, 1974.
В. Д. Мазуров.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
