ХАРДИ - ЛИТЛВУДА ПРОБЛЕМА
- ХАРДИ - ЛИТЛВУДА ПРОБЛЕМА
задача нахождения асимптотич. формулы для числа Q(n)решеий уравнения

где р - простое, хи у - целые, п - натуральное число  Аналогом этой задачи является проблема нахождения асимптотики для числа решений уравнения
Аналогом этой задачи является проблема нахождения асимптотики для числа решений уравнения

где  - фиксированное целое число,
- фиксированное целое число,
X. -Л. п. была поставлена Г. Харди (G. Hardy) и Дж. Литлвудом (J. Littlewood) в 1923 и рассмотрена ими на основе эвристич. и гипотетич. соображений.
Дисперсионный метод, разработанный Ю. В. Линником, позволил ему найти асимптотику для (1):
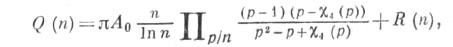
где

Из аналогичной формулы для (2) следует бесконечность множества простых чисел вида р=x2+y2+l. С помощью дисперсионного метода найдена асимптотика для числа решений обобщенного уравнения Харди - Литлвуда  где р - простое,
где р - простое,  - заданная примитивная положительно определенная квадратичная форма.
- заданная примитивная положительно определенная квадратичная форма.
Рассмотрение аналогичного уравнения  приводит к доказательству бесконечности множества простых чисел вида
приводит к доказательству бесконечности множества простых чисел вида 
Теорема Виноградова - Бомбьери о распределении простых чисел в арифметич. прогрессиях в среднем также доставляет решение X.- Л. п., заменяя фактически расширенную гипотезу Римана теоремами типа большого решета.
Лит.:[1] Линник Ю. В., Дисперсионный метод в бинарных аддитивных аадачах, Л., 1961; [2] Брeдихин Б. М., Линник Ю. В.. лМатем. сб.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Полезное
Смотреть что такое "ХАРДИ - ЛИТЛВУДА ПРОБЛЕМА" в других словарях:
Проблема Варинга — В 1770 г. Варинг выдвинул гипотезу[1], что при каждом целом существует такое число , что всякое натуральное число может быть представлено в виде с целыми неотрицательными . Эта гипотеза получила название проблема Варинга. Сегодня так на … Википедия
АНАЛИТИЧЕСКАЯ ТЕОРИЯ ЧИСЕЛ — раздел теории чисел. В А. т. ч. включают вопросы распределения простых чисел, аддитивные проблемы, исследование поведения теоретико числовых функций, теорию алгебраических и трансцендентных чисел. Распределение простых чисел, а) Одной из… … Математическая энциклопедия
АДДИТИВНАЯ ТЕОРИЯ ЧИСЕЛ — раздел теории чисел, в к ром изучаются задачи о разложении целых чисел на слагаемые заданного вида, а также алгебраич. и геометрич. аналоги таких задач, относящиеся к полям алгебраич. чисел и к множествам точек решетки. Эти задачи наз.… … Математическая энциклопедия
АДДИТИВНЫЕ ПРОБЛЕМЫ — проблемы теории чисел о разложении целых чисел на слагаемые заданного вида. Решение классич. А. п. привело к созданию новых методов в теории чисел. К классич. А. п. относятся: 1) Гольдбаха проблема о представлении нечетных натуральных чисел,… … Математическая энциклопедия
ДИСПЕРСИОННЫЙ МЕТОД — в теории чисел метод для решения нек рых бинарных уравнений (бинарных аддитивных проблем )вида где a и b принадлежат к достаточно густым и хорошо распределенным в арифметич. прогрессиях последовательностям натуральных чисел. Д. м., разработанный… … Математическая энциклопедия
Чисел теория — наука о целых числах. Понятие целого числа (См. Число), а также арифметических операций над числами известно с древних времён и является одной из первых математических абстракций. Особое место среди целых чисел, т. е. чисел..., 3 … Большая советская энциклопедия
Открытые проблемы в теории чисел — Теория чисел это раздел математики, занимающийся преимущественно изучением натуральных и целых чисел и их свойств, часто с привлечением методов математического анализа и других разделов математики. Теория чисел содержит множество проблем,… … Википедия
МЕТРИЧЕСКАЯ ТЕОРИЯ ЧИСЕЛ — раздел теории чисел, в к ром изучаются и метрически (т. е. на основе теории меры )характеризуются множества чисел, обладающих определенными арифметич. свойствами. М. т. ч. тесно связана с теорией вероятностей, что иногда дает возможность… … Математическая энциклопедия
ДИОФАНТОВА ГЕОМЕТРИЯ — диофантов анализ, область математики, посвященная изучению целочисленных и рациональных решений систем алгебраич. уравнений, или, иначе, изучению диофантовых уравнений, методами алгебраич. геометрии. Появление во 2 й пол. 19 в. теории алгебраич.… … Математическая энциклопедия
Линник — I Линник Владимир Павлович [р. 24.6(6.7).1889, Харьков], советский физик, академик АН СССР (1939). Окончил Киевский университет (1914). С 1926 работает в Государственном оптическом институте. Профессор ЛГУ (с 1934). Первые работы Л. по… … Большая советская энциклопедия

 Аналогом этой задачи является проблема нахождения асимптотики для числа решений уравнения
Аналогом этой задачи является проблема нахождения асимптотики для числа решений уравнения 
 - фиксированное целое число,
- фиксированное целое число,
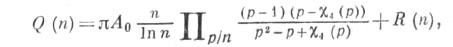

 где р - простое,
где р - простое,  - заданная примитивная положительно определенная квадратичная форма.
- заданная примитивная положительно определенная квадратичная форма.  приводит к доказательству бесконечности множества простых чисел вида
приводит к доказательству бесконечности множества простых чисел вида 
