ФРОБЕНИУСА ФОРМУЛА

- формула, выражающая отношение обобщенного определителя Вандермонда к обычному (см. Вандермонда определитель )через степенные суммы. В качестве коэффициентов в Ф. ф. участвуют характеры представлений симметрической группы.
Пусть x₁, ..., х _п- независимые переменные. Для любого набора неотрицательных целых чисел, удовлетворяющего условию пусть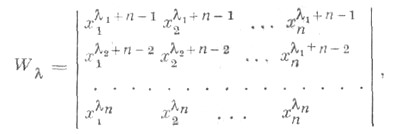

так что W₀ есть обычный определитель Вандермонда. И пусть тогда набор 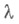после выкидывания нулей можно рассматривать как разбиение числа т. Рассматривается соответствующее неприводимое представление 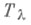группы S _т. Для любого разбиения числа тчерез обозначается значение характера представления 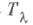на классе сопряженных элементов группы S_m,определяемом разбиением 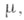и через 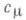- порядок централизатора любой подстановки из этого класса. Пусть где 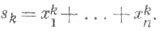Тогда

где сумма берется по всем (неупорядоченным) разбиениям числа т. При этом, если разбиение m содержит k₁ единиц, k₂ двоек и т. д., то

Если то Ф. ф. может быть преобразована к виду

где сумма берется по всем разбиениям числа . (дополненным надлежащим числом нулей). Последняя формула может быть использована для вычисления характеров симметрич. группы. А именно, 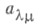есть коэффициент при в многочлене

Лит.:[1] Мурнаган Ф. Д., Теория представлений групп, пер. о англ., М., 1950.
Э. Б. Винберг.