- ФАДДЕЕВА УРАВНЕНИЕ
- линейное интегральное уравнение квантовой механики, описывающее рассеяние трех частиц.
Рассеяние трех частиц имеет по сравнению с рассеянием двух частиц принципиальное отличие, обусловленное возможностью образования связанных состояний частиц. Поэтому обычное условие излучения на бесконечности типа условия Зоммерфельда здесь неприменимо.
Математич. исследование трехчастичных систем стало возможным после того, как Л. Д. Фаддеев в 1960 предложил и изучил интегральное уравнение, по решениям к-рого восстанавливаются решения уравнения Шрёдингера, отвечающие правильным физич. условиям на бесконечности.
В сокращенной векторной записи Ф. у. имеет вид:
где
Е - энергия системы, Vi- потенциалы парного взаимодействия частиц, а вектор-функция Х 0 определяется начальными данными рассеяния. Если задача рассеяния сформулирована в терминах уравнения Шрёдингера с правой частью 
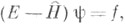где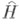 
-трехчастичный гамильтониан 
то следует выбрать в (*)
Тогда решение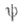 
задачи рассеяния выражается через решение XФ. у. по формуле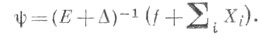 
При соответствующих ограничениях на потенциалы Vi уравнение (*) - фредгольмовского типа (см. [1]). Кроме того, с помощью уравнения (*) доказана теорема разложения по собственным функциям оператора Шрёдингера, дано обоснование нестационарной постановки задачи рассеяния, построен унитарный оператор рассеяния.
Ф. у. широко применяется в атомной и ядерной физике и в физике элементарных частиц. Получены релятивистский вариант этого уравнения и обобщение на случай системы Nчастиц. Важным преимуществом Ф. у. по сравнению с уравнением Шрёдингера является возможность эффективного численного решения.Лит.: [1] Фаддеев Л. Д., Математические вопросы квантовой теории рассеяния для системы трех частиц, М.-Л., 1963; [2] Шмид Э., Цигельман X., Проблема трех тел вквантовой механике, пер. с англ., М., 1979.
В. П. Маслов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
