- ГАУССА МЕТОД
- метод последовательного исключения неизвестных для нахождения решений системы линейных уравнений, впервые описанный К. Гауссом [1]. Пусть дана система

где
 - элементы произвольного поля Р. Без ограничения общности можно считать, что
- элементы произвольного поля Р. Без ограничения общности можно считать, что 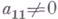 . Г. м. состоит в следующем. Из второго уравнения системы
. Г. м. состоит в следующем. Из второго уравнения системы  вычитают первое ее уравнение, умноженное почленно на
вычитают первое ее уравнение, умноженное почленно на 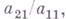 из третьего - первое, умноженное на
из третьего - первое, умноженное на  из m-го - первое, умноженное на
из m-го - первое, умноженное на  . Пусть
. Пусть 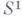 - система полученных уравнений-разностей. При наличии ненулевого коэффициента в
- система полученных уравнений-разностей. При наличии ненулевого коэффициента в  (после возможного изменения порядка уравнений и переменных) поступают с ней так же, как с системой
(после возможного изменения порядка уравнений и переменных) поступают с ней так же, как с системой  , и т. д. Если ранг r системы
, и т. д. Если ранг r системы 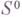 (т. е. ранг матрицы ее коэффициентов) меньше числа т, то на r-м шага появляется система
(т. е. ранг матрицы ее коэффициентов) меньше числа т, то на r-м шага появляется система 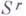 с нулевыми коэффициентами при всех неизвестных; при
с нулевыми коэффициентами при всех неизвестных; при  система
система  считается пустой. Система
считается пустой. Система 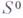 тогда и только тогда совместна, когда система
тогда и только тогда совместна, когда система 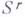 либо совместна (т. е. не имеет отличных от нуля свободных членов), либо пуста.
либо совместна (т. е. не имеет отличных от нуля свободных членов), либо пуста.
Процесс получения одного из решений (совместной) системы
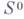 может быть описан следующим образом. Берется к.-л. решение
может быть описан следующим образом. Берется к.-л. решение  системы
системы 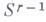 Придавая значения
Придавая значения  неизвестным
неизвестным  в к.-л. уравнении системы
в к.-л. уравнении системы 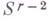 , имеющем ненулевой коэффициент при
, имеющем ненулевой коэффициент при  (напр., в первом ее уравнении), находят из него
(напр., в первом ее уравнении), находят из него 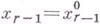 и получают решение
и получают решение 
 системы
системы 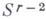 . Иначе говоря, значение
. Иначе говоря, значение  получается из системы
получается из системы  при замене в ней неизвестных
при замене в ней неизвестных  взятыми их значениями. Значения
взятыми их значениями. Значения 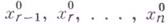 подставляются затем в систему
подставляются затем в систему 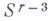 , находится значение
, находится значение 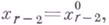 и получают решение
и получают решение  и т. д. Найденные так значения
и т. д. Найденные так значения 
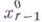 составляют вместе со взятыми значениями
составляют вместе со взятыми значениями 
 решение
решение 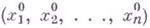 системы
системы 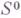 (см. [2]).
(см. [2]).
Описанный метод допускает следующее обобщение (см. [4]). Пусть U- нек-рое подпространство векторного пространства
 и
и 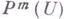 - множество всех решений
- множество всех решений  уравнения
уравнения

где хпробегает U. Для произвольной конечной системы
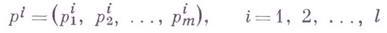
ненулевых образующих элементов пространства
 составляется система
составляется система
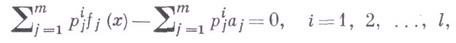
( х - неизвестное), наз. U-сверткой системы
 Если пространство
Если пространство 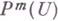 не содержит ненулевых элементов, то считается, что система
не содержит ненулевых элементов, то считается, что система 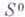 имеет пустую U-cвертку. Если система
имеет пустую U-cвертку. Если система 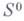 совместна, то при любом Uее U-свертка совместна или пуста. Установлено, что для совместности системы
совместна, то при любом Uее U-свертка совместна или пуста. Установлено, что для совместности системы  достаточно, чтобы совместной или пустой была ее U-свертка хотя бы для одного U. Пусть, далее,
достаточно, чтобы совместной или пустой была ее U-свертка хотя бы для одного U. Пусть, далее, 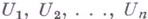 - подпространства,
- подпространства, 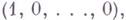 порождаемые
порождаемые  в пространстве
в пространстве 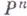 векторами. e1=(1,0, ..., 0), e2=(0,1, ... , 0), ... , en=(0,0, ... ,1).
векторами. e1=(1,0, ..., 0), e2=(0,1, ... , 0), ... , en=(0,0, ... ,1).
Для
 уравнение (*) сводится к уравнению
уравнение (*) сводится к уравнению

Пусть, напр.,
 . Если при этом
. Если при этом  то в качестве ненулевых образующих элементов пространства
то в качестве ненулевых образующих элементов пространства 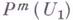 можно взять векторы
можно взять векторы 
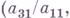

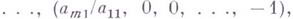 и тогда
и тогда 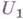 -свертывание системы
-свертывание системы 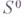 совпадает с процедурой исключения неизвестного
совпадает с процедурой исключения неизвестного 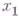 в Г. м.
в Г. м.
U-свертывание системы
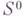 при
при 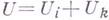 есть процедура одновременного исключения двух неизвестных
есть процедура одновременного исключения двух неизвестных  и
и  . Пусть, напр.,
. Пусть, напр., 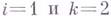 . Если при этом
. Если при этом
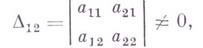
то для получения
 -свертки системы S0 можно взять строки матрицы
-свертки системы S0 можно взять строки матрицы
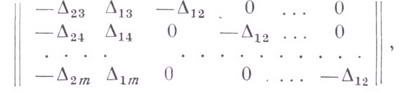
где
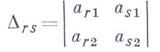
Чередуя исключения отдельных неизвестных с исключением тех или иных пар (или в общем случае наборов) неизвестных, можно для нахождения решений системы S0 строить те или иные алгоритмы, обобщающие Г. м. Лит.:[1] Gauss С. P., Beitrage zur Theorie der algebraischen Gleictumgen, Gott., 1849; И Курош А. Г., Курс высшей алгебры, 10 изд., М., 1971; [3] Фаддеев Д. К., Фаддеева В. Н., Вычислительные методы линейной алгебры, 2 изд , М.-Л., 1963; [4] Черников С. Н., Линейные неравенства, М., 1968. . С. Н. Черников.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
