- УИТТЕКЕРА ФУНКЦИИ
- функции
и 
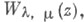к-рые являются решениями дифференциального Уиттекера уравнения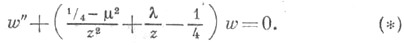 
Функция
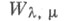вводится равенством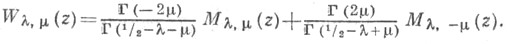 
Пары функций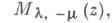
и 
и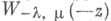 
- линейно независимые решения уравнения (*). Точка z=0 - точка ветвления для 
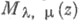и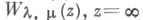 
- существенно особая точка.
Связь с другими функциями: С вырожденной гипергеометрической функцией:
с модифицированной Бесселя функцией и Макдональда функцией: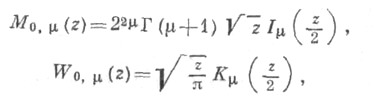
с интегралом вероятности:
с Лагерра многочленами: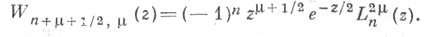
Лит.:[1] Бейтмен Г., Эрдейи А., Высшие трансцендентные функции, пер. с англ., [2 изд.], т. 2, М., 1974; [2] Уиттекер Э. Т., Ватсон Дж. Н., Курс современного анализа, пер. с англ., 2 изд., ч. 2, М., 1963.
Ю. А. Брычков, А. П. Прудников.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
