УЗЛОВ И ЗАЦЕПЛЕНИЙ ДИАГРАММЫ

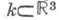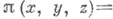
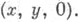графическое изображение узлов и зацеплений, основу к-рых составляют плоские проекции. Пусть - зацепление и - проекция Порядком точки наз. число элементов множества 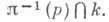Точки порядка два наз. двойными, точки порядка >1 - кратными. Говорят, что полигональное зацепление kнаходится в регулярном положении, если: (1) все его кратные точки являются двойными и их число конечно и (2) никакая двойная точка не является образом вершины. Всякое зацепление может быть переведено в регулярное положение сколь угодно малым вращением пространства. Если kнаходится в регулярном положении, то в каждой двойной точке ветвь, лежащая выше (в направлении координаты z), наз. переходом, а ветвь, лежащая ниже,- проходом. Чтобы задать диаграмму зацепления, находящегося в регулярном положении, нужно указать его проекцию и разорвать образы проходов в двойных точках (см. рис. 1). Если зацепление ориентировано, т. е. заданы обходы компонент, то они указываются на диаграмме Dстрелками. Если при обходе каждой компоненты зацепления на ее проекции проходы и переходы чередуются, то диаграмма наз. альтернирующей. Зацепление, имеющее хотя бы одну альтернирующую диаграмму, наз. альтернирующим зацеплением (см. Альтернирующие узлы и зацепления).
Каждой области f_i, на к-рые проекция зацепления делит плоскость отвечает ее индекс v(f_i), равный суммарному числу обходов, совершаемых проекциями всех компонент зацепления вокруг произвольной внутренней точки f_i. При переходе к смежной области индекс меняется на единицу, откуда следует, что все области f_i можно раскрасить в черный и белый цвета в шахматном порядке.

Во множество диаграмм на плоскости вводится некрое отношение эквивалентности, причем две диаграммы оказываются эквивалентными тогда и только тогда, когда отвечающие им зацепления объемлемо изотопны. Это дает возможность свести изучение узлов к плоской топологии. Именно, если D₁ можно получить из D₂ применением конечного числа элементарных операций I, II, III, показанных на рис. 2, и изотопич. деформаций. Подход к теории узлов, основанный на указанном сведении, является типичным подходом комбинаторной топологии. Он был основным в 1-й период развития теории узлов (примерно до 40-х гг. 20 в.). В рамках этого подхода инварианты узлов определяют исходя из диаграмм, а затем доказывают, что результат не зависит от выбора диаграммы (см. [1]). В современных исследованиях определения инвариантов предпочитают давать в терминах алгебраич. топологии, выделяя тем самым на первый план их геометрич. сущность.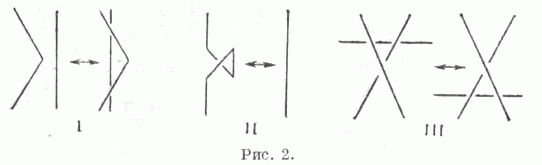

Диаграмма ориентированного зацепления используется для построения его поверхности Зейферта. Пусть х - произвольная не двойная точка ориентированной диаграммы Dзацепления k. Обход D, начиная от х, совершается в направлении, указанном ориентацией. В первой встретившейся двойной точке осуществляется поворот и продолжается движение в направлении ориентации Dдо возвращения в х;при этом будет описан простой замкнутый контур, к-рый наз. окружностью Зейферта. Диаграмма Dраспадается на такие окружности Зейферта С _j, причем они могут лишь соприкасаться. Пусть для каждой окружности С _j через D_j обозначается диск, лежащий в плоскости, параллельной 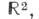так что его край проектируется в С _j. Для каждой двойной точки 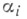рассматривается прямоугольник H_i, помещенный вертикально над 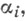к-рый скручивается на 90