ТОПОЛОГИЯ МНОГООБРАЗИЙ

- часть теории многообразий, посвященная в основном исследованию взаимоотношений между различными их типами.
Главнейшие типы конечномерных многообразий и взаимоотношения между ними можно изобразить схемой (1), в которой Diff - категория дифференцируемых (гладких) многообразий; PL - категория кусочно линейных (комбинаторных) многообразий; TRI - категория топологических многообразий, являющихся полиэдрами; Handle - категория топологических многообразий, допускающих топологическое разложение на ручки; Lip - категория липшицевых многообразий (с липшицевыми отображениями перехода между локальными картами);
ТОР - категория топологич. многообразий (хаусдорфовых и со счетной базой); Н -категория полиэдральных гомологич. многообразий без края (полиэдров, край звезды каждой вершины к-рых имеет гомологии сферы соответствующей размерности); H(ANR)-категория обобщенных многообразий (конечномерных абсолютных окрестностных ретрактов X, к-рые являются гомологич. многообразиями без края, т. е. 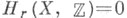обладают тем свойством, что для любой точки группа изоморфна группе P(ANR) - категория пространств Пуанкаре (конечномерных абсолютных окрестностных ретрактов X, для которых существует такое число пи такой элемент что при 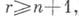и отображение при всех rявляется изоморфизмом); Р - категория полиэдров Пуанкаре (подкатегория предыдущей категории, состоящая из полиэдров). Стрелки схемы (1), кроме трех нижних и стрелок изображают функторы структуры забывания. Стрелка изображает теорему Уайтхеда о. триангулируемости гладких многообразий. В размерностях <8 эта стрелка обратима (любое PL-многообразие сглаживаемо), но в размерностях существуют несглаживаемые PL-многообразия и даже PL-многообразия, гомотопически неэквивалентные никакому гладкому многообразию. Вложение также необратимо в том же сильном смысле (существуют полиэдральные многообразия размерности гомотопически неэквивалентные никакому PL-многообразию). При этом уже для сферы Sⁿ, существуют триангуляции, в к-рых она не является PL-многообразием.

Стрелка изображает тот факт, что любое PL-многообразие допускает разложение на ручки. Стрелка 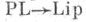изображает теорему о существовании на произвольном PL-многообразии липшицевой структуры.
Стрелка обратима при 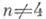и необратима при n=4 (любое топологическое многообразие размерности 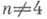допускает разложение на ручки, и существуют четырехмерные топологич. многообразия, для к-рых это не так).
Аналогично, при обратима стрелка (и притом единственным образом).
Вопрос об обратимости стрелки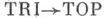 составляет классическую нерешенную задачу о триангулируемости произвольных топологич. многообразий.
Стрелка необратима в сильном смысле (существуют полиэдры Пуанкаре, гомотопически неэквивалентные никакому гомологич. многообразию).
Стрелка изображает теорему о гомотопической эквивалентности любого гомологич. многообразия размерности топологич. многообразию.
Стрелка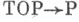 изображает теорему Кёрби - Зибенмана о гомотопич. эквивалентности любого топологич. многообразия полиэдру.
Вложение изображает тот факт, что любое топологич. многообразие является ANR. Обобщенное многообразие 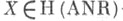размерности тогда и только тогда принадлежит образу этого вложения, когда Xобладает свойством раздвижки дисков (для любого и любых отображений где В ² -двумерный диск, существуют такие отображения что и

Аналогичный вопрос для стрелок решается с помощью теории стационарных расслоений (соответственно векторных, кусочно линейных, топологических и сферических), т. е. на основе рассмотрения гомотопических классов отображений многообразия Xв соответствующие классифицирующие пространства ВО, BPL, ВТОР, BG.
Существуют сквозные канонич. отображения

гомотопич. слои к-рых и их композиций обозначаются соответственно символами PL/O, ТОР/О, G/0, TOP/PL, G/PL, G/TOP. Для каждого многообразия Xлюбой из категорий Diff, PL, TOP, P существует нормальное стационарное расслоение, т. е. канонич. отображение t _х многообразия Xв соответствующее классифицирующее пространство.
При переходе от лузкой